آنالیز هارمونیک
آنالیز هارمونیک شاخه ای از ریاضیات است که مرتبط با نمایش توابع یا سیگنال ها به صورت برآیندی از امواج پایه بوده و به مطالعه و نمایش مفاهیم سری های فوری و تبدیل فوریه (یعنی فرم توسعه یافته ی آنالیز فوریه) می پردازد. در دو قرن اخیر، این شاخه به شاخه ای وسیع تبدیل شده که کاربرد های گسترده ای در نظریه اعداد، نظریه نمایش، پردازش سیگنال، مکانیک کوانتومی، آنالیز جزر و مدی و علوم اعصاب دارد.
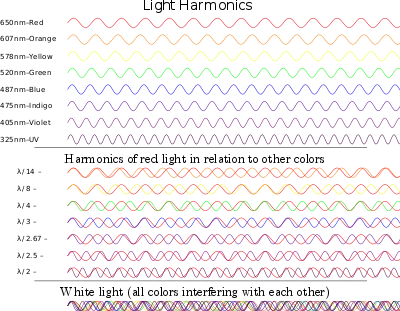
عبارت "هماهنگ ها" (به انگلیسی harmonics) از ریشه یونانی harmonikos به معنای "ماهر در موسیقی" گرفته شده است.[1] در مسائل فیزیکی مقدار ویژه ای، این که فرکانس یک موج ضرایب صحیحی از موج دیگری باشد، معنا دار شد، مثل هماهنگ های نوت های موسیقیایی، اما این اصطلاح (هماهنگ) کاربرد هایی فراتر از معنی اصلی آن پیدا کرد.
تبدیل فوریه کلاسیک روی هنوز هم یک حوزه زنده تحقیقاتیست، بخصوص تبدیل های فوریه روی اشیاء کلی تری چون توزیعات تمپرد. به عنوان مثال، اگر ما برخی الزامات روی توزیعی چون اعمال کنیم، می توانیم آن ها را به زبان تبدیل فوریه روی نیز ترجمه کنیم. قضیه پالی-وینر مثالی ازین فرایند است. قضیه پالی-وینر فوراً ایجاب می کند که اگر یک توزیع ناصفر با تکیه گاهی فشرده باشد (شامل توابع با تکیه گاه ثابت هم می شود)، آنگاه تبدیل فوریه آن هیچ گاه تکیه گاه فشرده نخواهد داشت. این حالت بسیار مقدماتی از اصل عدم قطعیت در بستر آنالیز-هارمونیک است.
سری های فوری را می توان در بستر فضاهای هیلبرت به طور مناسب تری مطالعه کرد، چرا که در آنجا ارتباطی بین آنالیز هارمونیک و آنالیز تابعی ارائه می کند.
آنالیز هارمونیک کاربردی
.png.webp)
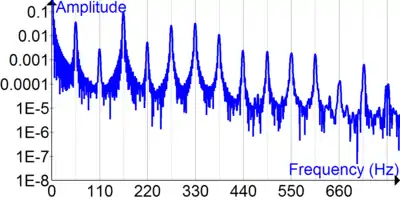
بسیاری از کاربرد های آنالیز هارمونیک در علم و مهندسی با ایده یا فرضی شروع شد که یک پدیده یا سیگنال را می توان به صورت ترکیبی از جمع تک مؤلفه های ارتعاشی در نظر گرفت. جزر و مد اقیانوس و ریسمان مرتعش مثال های رایج و ساده ای هستند. اغلب رهیافت های نظری سعی می کنند با معادلات دیفرانسیل یا دستگاهی از معادلات استفاده کنند تا ویژگی های اساسی سیستم شامل دامنه، فرکانس و فاز های مؤلفه های ارتعاشی را توصیف کنند. معادلات خاصی به نوع میدان وابستگی دارند، اما نظریه ها عموماً سعی می کنند معادلاتی انتخاب کنند که نمایانگر اصول اصلی قابل کاربرد باشند.
رهیافت آزمایشی اغلب نیازمند داده هایی اند که به طور دقیق پدیده مورد نظر را ارزیابی کند. به عنوان مثال، در مطالعه جزر و مد، آزمایشگر ممکن است نمونه هایی از عمق آب را به صورت تابعی از زمان جمع آوری کند به گونه ای که بازه های فضایی به میزان کافی به هم نزدیک باشند تا هر نوسان در بازه زمانی به اندازه کافی بلند برای مشاهده چندین دوره نوسانی باشد.
به عنوان مثال، سیگنال تصویر بالایی یک موج صوتی گیتار باس است که با در آن نوت A با ریسمان باز با فرکانس پایه ای 55 هرتزی نواخته شده است. شکل موج حالت نوسانی دارد، اما پیچیده تر از یک موج ساده سینوسی است، که نشانگر حضور امواج دیگری در آن می باشد. مؤلفه های مختلف موج را می توان با اعمال تکنیک های آنالیز ریاضیاتی به نام تبدیل فوریه شناسایی کرد، نتیجه این تبدیل در تصویر پایینی نشان داده شده. توجه کنید که در فرکانس 55 هرتز پیک عمده ای مشاهده می شود، اما پیک های دیگری در فرکانس های 110 و 165 هرتز و فرکانس های دیگر مرتبط با آن دیده می شود که ضرایبی از 55 هرتز هستند. در این حالت فرکانس 55 هرتز به عنوان فرکانس بنیادی ریسمان مرتعش شناسایی شده و به ضرایب صحیحی که در آن ضرب می شود هماهنگ ها می گویند.
کتابشناسی
- Elias Stein and Guido Weiss, Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, 1971. شابک ۰−۶۹۱−۰۸۰۷۸-X
- Elias Stein with Timothy S. Murphy, Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Princeton University Press, 1993.
- Elias Stein, Topics in Harmonic Analysis Related to the Littlewood-Paley Theory, Princeton University Press, 1970.
- Yitzhak Katznelson, An introduction to harmonic analysis, Third edition. Cambridge University Press, 2004. شابک ۰−۵۲۱−۸۳۸۲۹−۰ ; 0-521-54359-2
- Terence Tao, Fourier Transform. (Introduces the decomposition of functions into odd + even parts as a harmonic decomposition over ℤ₂.)
- Yurii I. Lyubich. Introduction to the Theory of Banach Representations of Groups. Translated from the 1985 Russian-language edition (Kharkov, Ukraine). Birkhäuser Verlag. 1988.
- George W. Mackey, Harmonic analysis as the exploitation of symmetry–a historical survey, Bull. Amer. Math. Soc. 3 (1980), 543–698.