تنسور

تنسور (به انگلیسی: Tensor) عنصری هندسی است که در ریاضی و فیزیک به منظور گسترش مفاهیم اسکالرها، بردارها و ماتریس‌ها به ابعاد بالاتر معرفی می‌شوند. تنسورها اولین بار توسط تولیو لوی-چیویتا و گرگریو ریتچی-کورباسترو ابداع شدند. در واقع کار آن‌ها ادامه کارهای برنهارت ریمان و الوین برونو کریستوفل و دیگران در حساب دیفرانسیل مطلق بود.

تنسور تنش کشی, یک تنسور مرتبه دو است. اجزای تنسور، در یک سیستم مختصات دکارتی سه بعدی،ماتریس
${\displaystyle {\begin{aligned}\sigma &={\begin{bmatrix}\mathbf {T} ^{(\mathbf {e} _{1})}\mathbf {T} ^{(\mathbf {e} _{2})}\mathbf {T} ^{(\mathbf {e} _{3})}\\\end{bmatrix}}\\&={\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}\\\end{aligned}}}$
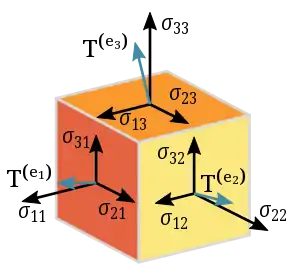
را تشکیل می دهند. که ستون‌ها تنش های(forces per unit area) روی صفحه‌های e₁, e₂, و e₃ مکعب است.

تنسور آرایه‌ای است از اعداد که در یک جدول چیده شده‌اند. این جدول در حالت کلی می‌تواند به صورت ${\displaystyle M\times N\times O\times P\times ...}$ باشد که حروف بزرگ هر کدام می‌توانند نمایندهٔ یک عدد طبیعی باشند و ${\displaystyle \times }$ نشان دهندهٔ عمل ضرب بین آنهاست. تنسور در ساده‌ترین حالت می‌تواند یک عضو داشته باشد که به آن تنسور، اسکالر گوییم. در حالت کمی پیشرفته تر تنسور می‌تواند به صورت بردار باشد. یعنی وقتی شما بردار ${\displaystyle A}$ را به صورت ${\displaystyle (x,y,z)}$ نشان می‌دهید در حقیقت یک تنسور دارید. در حالتی باز هم پیشرفته تر تنسور می‌تواند دو بعدی باشد (به صورت ماتریسی). یعنی مثلاً جدول ما ${\displaystyle 2\times 2}$ باشد یعنی دو سطر و دو ستون داشته باشد.

چنین تنسوری دارای ۴ عضو است. به‌طور کلی تنسورهای دو بعدی و بالاتر از دو بعد را با نام ماتریس هم می‌شناسند. ماتریس‌ها از آن جهت مورد استفاده قرار می‌گیرند که باعث ایجاد نظم بین داده‌های یک مسئله و دسته بندی اطلاعات آن می‌شوند.

تعریف فوق همراه با ساده‌سازی است. یک تعریف دقیق‌تر از این قرار است:

یک تنسور رتبه (۰,۱) و ${\displaystyle N}$-بعدی حقیقی مانند ${\displaystyle T}$ نگاشتی است خطی از ${\displaystyle \mathbb {R} ^{N}}$ به ${\displaystyle \mathbb {R} }$ یعنی:

${\displaystyle T(ax+by)=aT(x)+bT(y),\qquad \forall x,y\in \mathbb {R} ^{N}{\hbox{ and }}a,b\in \mathbb {R} .}$

اگر ${\displaystyle \{e_{n}\}_{n=1}^{n=N}}$ یک پایه برای ${\displaystyle \mathbb {R} ^{N}}$ باشد، آنگاه به مجموعه ${\displaystyle N}$ عدد ${\displaystyle T_{n}}$ که از

${\displaystyle T(e_{n})=T_{n}}$

به دست می‌آیند مؤلفه‌های ${\displaystyle T}$ در پایه ${\displaystyle \{e_{n}\}_{n=1}^{n=N}}$ می‌گویند. می‌توان دید که مؤلفه‌های این تنسور، تحت تغییر پایه، رفتاری شبیه مؤلفه‌های یک بردار پادهموردا دارند. با یک نگاه کلی‌تر می‌توانیم ${\displaystyle \mathbb {R} ^{N}}$ را با یک فضای برداری ${\displaystyle N}$-بعدی دلخواه چون ${\displaystyle V}$ عوض کنیم. در این صورت معمول است که مجموعهٔ همه چنین تنسورهایی را با ${\displaystyle V^{*}}$ نشان دهیم.

به‌طور مشابه یک تنسور رتبه (۰,۲) به عنوان یک نکاشت دو-خطی از ${\displaystyle V\times V}$ به ${\displaystyle \mathbb {R} }$ تعریف می‌شود:

${\displaystyle T(ax+by,z)=aT(x,z)+bT(y,z),\qquad \forall x,y,z\in V{\hbox{ and }}a,b\in \mathbb {R} ,}$ ${\displaystyle T(z,ax+by)=aT(z,x)+bT(z,y),\qquad \forall x,y,z\in V{\hbox{ and }}a,b\in \mathbb {R} .}$

این بار به مجموعه ${\displaystyle N^{2}}$ عدد ${\displaystyle T_{m,n}}$ که با

${\displaystyle T(e_{m},e_{n})=T_{m,n}}$

تعریف می‌شوند مؤلفه‌های تنسور ${\displaystyle T}$ گفته می‌شود (${\displaystyle \{e_{n}\}_{n=1}^{n=N}}$ پایهٔ ${\displaystyle V}$ است). مجموعه تمام این تنسورها را با ${\displaystyle V^{*}\otimes V^{*}}$ نشان می‌دهیم و می‌نویسیم: ${\displaystyle T\in V^{*}\otimes V^{*}}$.

یک تنسور (۱,۰) چون ${\displaystyle T}$ عضوی است از فضای برداری ${\displaystyle V}$. مؤلفه‌های این تنسور با شاخص‌های بالا و بدین ترتیب تعریف می‌شوند:

${\displaystyle T=\sum _{n=1}^{n=N}T^{n}e_{n}}$

یک تنسور (۲,۰) عضوی از فضای برداری ${\displaystyle V\otimes V}$ است که با پایه‌های ${\displaystyle e_{m}\otimes e_{n}}$ تولید می‌شود. بنابراین چنین تنسوری با

${\displaystyle T=\sum _{m,n=1}^{N}T^{mn}e_{m}\otimes e_{n}}$

داده می‌شود و ${\displaystyle T^{mn}}$ مؤلفه‌های آن نامیده می‌شوند.

کتابخانه‌های نرم‌افزاری مبتنی بر تنسور

در سال‌های اخیر به منظور سهولت استفاده از تنسورها و همچنین پردازش سریع آن‌ها، کتابخانه‌هایی برای استفاده در زبان‌های برنامه‌نویسی توسعه داده شده‌اند. از این جمله می‌توان به تنسورفلو (TensorFlow) اشاره کرد.[1] همچنین گوگل مدار مجتمع با کاربرد خاصی را با نام واحد پردازشگر تانسوری (به اختصار: TPU) جهت انجام بهینه و سریعتر محاسبات تانسوری برای شبکه‌های عصبی گسترش داده است.

منابع

1. "درجه، بعد و شکل تنسورها در TensorFlow". یادگیری ماشین در TensorFlow. Retrieved 2019-01-11.

• Dubrovin, B. A., Fomenko, A. T., and Novikov, S. P. Modern Geometry - Methods and Applications, Second Edition, Springer-Verlag, New York, 1992 ISBN 3-540-97663-9