نظریه اطلاعات

نظریه اطلاعات[1] (انگلیسی: Information theory)، به مقداردهی (Quantification)، ذخیره و انتقال اطلاعات می‌پردازد. این نظریه، مدلی ریاضی از شرایط و عوامل مؤثر در پردازش و انتقال اطلاعات (داده‌ها) به‌دست می‌دهد. تمرکز این نظریه بر محدودیت‌های بنیادین ارسال و پردازش اطلاعات است، و کمتر به چگونگی عملکرد و پیاده‌سازی روش‌های انتقال و پردازش اطلاعات می‌پردازد. پیدایش این نظریه در پی کارهای کلود شانون در ۱۹۴۸ بوده‌است.

نظریه اطلاعات
مفاهیم
آنتروپی اطلاعات اطلاعات مشترک نرخ مخابره ظرفیت کانال
چهره‌های مهم
کلود شانون هری نایکویست رالف هارتلی توماس کاور رابرت فانو ریچارد همینگ رابرت گالاگر رادلف السوده آرون واینر
جوایز مهم
جایزه کلود شانون

نظریه اطلاعات مورد استفاده خاص مهندسان مخابرات است، هرچند برخی از مفاهیم آن در رشته‌های دیگری مانند روان‌شناسی، زبان‌شناسی، کتاب‌داری و اطلاع‌رسانی، و علومِ شناختی (Cognitive Sciences) نیز استفاده می‌شود.[2]

مفهوم «اطلاعات» که شانون پیش نهاد، از دیدگاه آمار و احتمالات بوده و لزوماً با مفهوم رایج اطلاعات به معنی «دانش» یا دیگر استفاده‌های روزمره از آن در زبان محاوره‌ای مانند «بازیابی اطلاعات»، «تحلیل اطلاعات»، «چهارراه اطلاعات» و غیره یکی نیست. اگر چه نظریه اطلاعات بر رشته‌های دیگر مانند روان‌شناسی و فلسفه اثر گذاشته، ولی اثرش به علت مشکل تبدیل «مفهوم آماری اطلاعات» به «مفهوم معنایی دانش و محتوا» بیشتر از نوع القای احساساتی نسبت به مفهوم اطلاعات بوده‌است.[3]

تاریخچه

اختراع تلگراف و پس از آن تلفن، توجه به مفهوم اطلاعات و انتقال آن را افزایش داد. در ۱۸۴۴، ساموئل مورس خط تلگرافی میان واشینگتن و بالتیمور در آمریکا برپا کرد. مورس در ارسال اطلاعات به مشکلات الکتریکی عملی برخورد. او دریافت که خطوط انتقالی که زیرِ زمین کشیده شده‌اند مشکلات بیشتری از خطوط انتقال هوایی (روی تیر) دارند و این خود زمینه‌ای برای تحقیقات بعدی شد. با اختراع تلفن توسط الکساندر گراهام بل در ۱۸۷۵ و گسترش آن، برخی به بررسی مشکلات انتقال اطلاعات پرداختند. بیشتر این تحقیقات از تبدیل فوریه استفاده کرده، اما تمرکز آن‌ها بیشتر روی جنبه عملی و مهندسی موضوع بود.[2]

تحقیق دربارهٔ نظریه اطلاعات نخستین بار در ۱۹۲۴ از سوی هری نایکوئیست در مقاله‌ای به نام «عوامل خاصی که بر سرعت تلگراف اثر می‌گذارند» آغاز شد. او به بیشترین نرخ ارسال اطلاعات پی برد و فرمولی برای محاسبه آن پیش نهاد. کار مهم دیگر در آن زمان، مقاله «انتقال اطلاعات» در ۱۹۲۸ از سوی هارتلی بود که نخستین پایه‌های ریاضی نظریه اطلاعات را بنا گذاشت.[2]

کلود شانون

تولد واقعی نظریه اطلاعات را می‌توان به مقاله «نظریه ریاضی مخابرات» از سوی کلود شانون نسبت داد. یکی از نکات اصلی مقاله شانون توجه به این نکته بود که بررسی سیگنال‌های مخابراتی را باید از بررسی اطلاعاتی که حمل می‌کنند جدا کرد، در حالی که پیش از او چنین نبود. شانون همچنین به این نکته توجه کرد که طول یک سیگنال همیشه متناسب با میزان اطلاعات آن نیست. مثلاً نقل شده‌است که در نامه‌ای که ویکتور هوگو به ناشرش نوشت، فقط «؟» نوشته بود و در پاسخ نامه‌ای دریافت کرد که فقط «!» در آن بود. این دو نماد برای هر دو طرف معنی داشتند، هرچند از دید ناظری که معنی آن‌ها را نمی‌دانست، مبهم بودند. مثال دیگر، جمله‌ای طولانی است که به زبان فارسی نوشته شده‌است، ولی برای انگلیسی‌زبانی که فارسی نمی‌داند مفهومی ندارد. بدین‌سان شانون پیشنهاد کرد که مسئله ارسال سیگنال را از ارسال اطلاعات موجود در آن جدا کرده، و برای موضوع اول نظریه ریاضی ارائه کرد.[2]

شانون در آن زمان در آزمایشگاه‌های بل کار می‌کرد و سعی در طراحی خطوط تلفن با ضریب اطمینان بالا داشت. پیش از شانون عوامل مؤثر در استفاده بهینه از خطوط تلفن شناخته نشده بود و بیشترین تعداد مکالمات تلفنی که می‌توان روی خطوط تلفن منتقل کرد نامشخص بود. شانون پس از ارائه تعریفی ریاضی از کانال مخابراتی، ظرفیتی به کانال مخابراتی نسبت داد که بیانگر بیشترین میزان اطلاعاتی است که می‌توان روی کانال مخابره کرد. فرمول ظرفیت کانال شانون نه تنها برای کانال‌های بینویز، بلکه برای کانال‌های نویزدار هم قابل استفاده بود. او فرمولی پیش نهاد که اثر پهنای باند کانال، و نسبت توان سیگنال به توان نویز (نسبت سیگنال به نویز) را بر ظرفیت کانال نشان می‌داد.[2]

مفهوم اطلاعات و راه‌های اندازه‌گیری آن

مفهوم اطلاعاتی که توسط شانون مطالعه شد اطلاعات از دید «آمار و احتمالات» بوده و با مفاهیم روزمره از اطلاعات مانند «دانش» یا استفاده‌های روزمره از آن در زبان طبیعی مانند «بازیابی اطلاعات»، «تحلیل اطلاعات»، «چهارراه اطلاعات» و غیره تفاوت می‌دارد. اگر چه نظریه اطلاعات رشته‌های دیگر مانند روان‌شناسی و فلسفه را تحت تأثیر قرار داده، ولی به دلیل مشکلات تبدیل «مفهوم آماری اطلاعات» به «مفهوم معنایی دانش و محتوا» تأثیراتش بیشتر از نوع القای احساساتی نسبت به مفهوم اطلاعات بوده‌است.[3]

آمار و احتمالات نقشی حیاتی و عمده در ظهور و رشد نظریه اطلاعات برعهده دارد.

قضایای شانون

شانون در کارهایش، مسئله ارسال اطلاعات در یک کانال مخابراتی را به صورت پایه‌ای بررسی کرد، و مدل ریاضی کاملی برای منبع اطلاعات، کانال ارسال اطلاعات و بازیابی اطلاعات پیش نهاد. او مسئلهٔ ارسال اطلاعات از فرستنده (منبع اطلاعات) به گیرنده (مقصد اطلاعات) را به کمک احتمالات بررسی کرد. دو نتیجهٔ مهم، معروف به قضیه‌های شانون، عبارت‌اند از:

• حداقل نرخ فشرده‌کردن اطلاعات یک منبع تصادفی، برابر با آنتروپی آن منبع است؛ به عبارت دیگر نمی‌توان دنباله خروجی یک منبع اطلاعات را با نرخی کمتر از آنتروپی آن منبع ارسال کرد.
• حداکثر نرخ ارسال اطلاعات روی یک کانال مخابراتی، طوری‌که بتوان در مقصد، اطلاعات را با احتمال خطای در حد قابل قبول کم بازیافت، مقداری ثابت و وابسته به مشخصات کانال است، و ظرفیت کانال نام دارد. ارسال اطلاعات با نرخی بیشتر از ظرفیت کانال، به خطا می‌انجامد.

این دو نتیجه، به ترتیب به کُدینگ منبع (source coding) و کدینگ کانال (channel coding) می‌انجامند. از موضوعات مرتبط با کدینگ کانال، می‌توان به نظریه کدینگ جبری کانال (Algebraic coding theory) اشاره کرد.

بخش دیگری از کار شانون به مسئله امنیت انتقال اطلاعات (information security) می‌پردازد که ربط مستقیمی به دو نتیجه بالا ندارد و مبنای نظری رمزنگاری (cryptography) نوین است. به عبارت بهتر، مسئله اطمینان انتقال اطلاعات (information reliability) که با دو نتیجه بالا توصیف می‌شود را نباید با مسئله امنیت انتقال اطلاعات (information security) اشتباه گرفت؛ هدف این دو کاملاً متفاوت است.

کمیت‌های مربوط به اطلاعات

نظریه اطلاعات بر پایه نظریهٔ احتمالات و فرایندهای اتفاقی (Probability Theory and Stochastic Processes) شکل گرفته‌است. مهم‌ترین کمیت‌های مربوط به اطلاعات عبارتند از

• آنتروپی، که میانگین محتوای اطلاعاتی یک منبع اطلاعات است.
• اطلاعات متقابل، که مقدار اطلاعات مشترک دو متغیر تصادفی است.

آنتروپی نشان می‌دهد که اطلاعات خروجی یک منبع اطلاعات تا چه حد می‌تواند فشرده شود؛ در حالی که اطلاعات متقابل، نرخ انتقال اطلاعات در یک کانال مخابراتی را تعیین می‌کند.

رایج‌ترین واحد اطلاعات، بیت است که بر مبنای لگاریتم دودویی (باینری) است. دیگر واحدها شامل نَت (بر اساس لگاریتم طبیعی) و هارتلی (بر اساس لگاریتم معمولی) هستند. انتخاب مبنای لگاریتم، واحد آنتروپی اطلاعات را مشخص می‌کند.

در عبارت ${\displaystyle p\log p}$، زمانی که ${\displaystyle p=0}$ است، عبارت هم برابر صفر در نظر گرفته می‌شود، زیرا ${\displaystyle \lim _{p\rightarrow 0+}p\log p=0}$

آنتروپی

آنتروپی متغیر تصادفی برنولی به صورت تابعی از احتمال موفقیت، اغلب به نام تابع باینری آنتروپی نامیده می‌شود. ${\displaystyle H_{\mbox{b}}(p)}$. مقدار آنتروپی در ۱ بیشینه است.

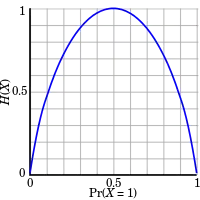
آنتروپی یک متغیر تصادفی، با اندازه‌گیری احتمالات آن متغیر تصادفی به‌دست می‌آید. مفهوم آنتروپی در طول دهه های گذشته دستخوش تغییرات شده و به کاربردهای مهمی در دیگر شاخه های علوم از جمله فشرده‌سازی داده‌ها، علوم اعصاب ، مهندسی مخابرات و کدگذاری کانال انجامیده است.

جستارهای وابسته

• اطلاعات
• فلسفه اطلاعات

پانویس

1. «نظریهٔ اطلاعات» [علوم کتابداری و اطلاع‌رسانی] هم‌ارزِ «information theory»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر ششم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۹۶۴-۷۵۳۱-۸۵-۶ (ذیل سرواژهٔ نظریهٔ اطلاعات)
2. «information theory," Encyclopædia Britannica
3. SAYRE, KENNETH M. (1998). Information theory. In E. Craig (Ed.), Routledge Encyclopedia of Philosophy. London: Routledge.

منابع

• مفاهیم معنائی اطّلاعات دائرةالمعارف فلسفهٔ استانفورد (انگلیسی)

Earl Morrogh, Information Architecture, An Emerging 21st Century Profession, Pearson Education, Inc. , 2003. ISBN 0-13-096746-7

پیوند به بیرون

• نظریه‌ای ریاضی برای مخابرات بایگانی‌شده در ۱۵ دسامبر ۲۰۱۷ توسط Wayback Machine مقاله ۱۹۴۸ کلاود شانون که سرآغاز نظریه اطلاعات به‌شمار می‌رود
• نظریه اطّلاعات از آزمایشگاه‌های بل