سری زمانی

تعریف سری زمانی

در علوم مختلف، به یک توالی یا دنباله از متغیرهای تصادفی که در فاصله های زمانی ثابت نمونه برداری شده باشند، اصطلاحاً سری زمانی یا پیشامد تصادفی در مقطع زمان می‌گویند. به عبارت دیگر منظور از یک سری زمانی مجموعه‌ای از داده‌های آماری است که در فواصل زمانی مساوی و منظمی جمع‌آوری شده باشند. روش‌های آماری ای که این گونه داده‌های آماری را مورد استفاده قرار می‌دهد مدل های تحلیل سری زمانی نامیده می‌شود. مانند فروش فصلی یک شرکت طی سه سال گذشته. یک سری زمانی مجموعهٔ مشاهدات تصادفی ای است که بر اساس زمان مرتب شده باشند. مثال‌های آن در اقتصاد و حتی رشته‌های مهندسی دیده می‌شود.

دنباله‌ای از داده‌ها که در یک محدود زمانی جمع‌آوری شده‌‌اند، یک سری زمانی را تشکیل می‌دهند. این داده‌ها تغییراتی که پدیده در طول زمان دچار شده را منعکس می‌کنند. بنابراین می‌توانیم این مقدارها را یک بردار وابسته به زمان بدانیم. در این حالت اگر X یک بردار باشد، سری زمانی را می‌توان به صورت زیر نشان داد؛ که در آن t، بیانگر زمان و X نیز یک متغیر تصادفی است.

X(t), t=1,2,3,...

طبق این تعریف زمان t=0 نیز قابل تعریف است. این لحظه می‌تواند زمان تولد یک پدیده یا هنگامی باشد که اولین اطلاعات در آن لحظه ثبت شده است. به این ترتیب (X(t متغیر تصادفی X را در زمان t‌ نشان می‌دهد. مقدارهای مشاهده شده این متغیر تصادفی دارای ترتیبی هستند که زمان وقوع هر داده را نشان می‌دهند.

اگر متغیر تصادفی X، یک بعدی باشد،‌ یعنی از بین ویژگی‌های مختلف یک پدیده فقط از یکی ویژگی برای ایجاد مدل سری زمانی استفاده شود، مدل را «یک متغیره» (Univariate) می‌نامند. ولی اگر از چندین ویژگی برای ایجاد مدل سری زمانی استفاده شود، مدل سری زمانی را «چند متغیره» (Multivariate) می‌گویند. البته اگر علاوه بر زمان، مکان یا مختصات را (یا هر اطلاعاتی که مقدار داده‌ها به آن وابسته باشند) به مدل اضافه کنیم، وارد مبحث «آمار فضایی» (Spatial Statistic) خواهیم شد.

روش‌های تحلیل

روش‌های تحلیل سری زمانی به دو دسته تقسیم می‌شوند: روش‌های دامنه فرکانس و روش‌های دامنه زمان. دسته اول شامل تحلیل طیفی و تحلیل موجک و دسته دوم شامل تحلیل‌های خودهمبستگی و همبستگی متقابل است.

افزون بر این می‌توان روش‌های تحلیل سری زمانی را به دو دسته پارامتری و ناپارامتری تقسیم کرد. در روش‌های پارامتری چنین انگاشته می‌شود که فرایند مانای احتمالاتی دارای ساختاری مشخص است که می‌توان آن را با تعداد اندکی پارامتر (از جمله با استفاده از مدل خودهمبسته یا میانگین متحرک) توصیف کرد. در این روش‌ها هدف تخمین پارامترهای مدلی است که فرایند احتمالاتی را توصیف می‌کند. در مقابل، روش‌های ناپارامتری صریحاً کوواریانس یا طیف فرایند را بدون در نظر گرفتن ساختاری مشخص برای آن تخمین می‌زنند. همچنین می‌توان روش‌های تحلیل سری زمانی را به دستهٔ روش‌های خطی و غیر خطی یا روش‌های تک‌متغیره و چندمتغیره تقسیم کرد. همچنین اگر تغییرات پدیده را در مدل سری زمانی برای زمان‌های منقطع در نظر بگیریم، سری را زمان-گسسته (Discreet Time) و برعکس اگر زمان را به صورت پیوسته در مدل فرض کنیم، سری را زمان-پیوسته (Continuous Time) می‌نامند. برای مثال ثبت دما، دبی رودخانه و … از گروه سری‌های زمان-پیوسته هستند و تعداد جمعیت، تولیدات کارخانه و … از نوع سری زمان- گسسته محسوب می‌شوند.

معمولا در سری زمان-گسسته، داده‌ها در مقاطع مشخصی از زمان مثل ساعت، روز یا هفته و حتی سال جمع‌آوری می‌شوند. غالباً ایجاد مدل‌ها برای سری‌های زمان-گسسته انجام می‌شود زیرا با استفاده از گروه‌بندی و ایجاد فاصله‌های زمانی ترتیبی، امکان تبدیل سری‌های زمانی-پیوسته به زمان-گسسته وجود دارد.

مولفه‌های یک سری زمانی

معمولا می‌توان الگوی رفتار یا مدل تغییرات یک سری زمانی را به چهار مولفه تفکیک کرد. «روند» (Trend)، «تناوب» (Cyclic)، «فصل» (Seasonal) و «تغییرات نامعمول» (Irregular). اگر نمودار مربوط به داده‌های سری زمانی را برحسب زمان ترسیم کنیم می‌توانیم این مولفه‌ها را تشخیص دهیم در نتیجه شناخت بهتری از داده‌های سری زمانی خواهیم داشت. در ادامه به معرفی و بررسی هر یک از این مولفه‌ها می‌پردازیم.

روند (Trend): تمایل سری زمانی به افزایش، کاهش یا حتی ثابت بودن، روند را تشکیل می‌دهد. در یک سری زمانی با روند افزایشی، انتظار داریم مقدارهای سری زمانی در زمان‌های t=1 و t=2 به صورت (X(1)≤X(2 باشند. برای مثال روند برای سری زمانی مربوط به میزان جمعیت یا سرمایه در بازار بورس به صورت افزایشی، ولی روند برای میزان مرگ و میر با توجه به پیشرفت در امور پزشکی، کاهشی است. در تصویرهای زیر سه نمودار مربوط به سه سری زمانی در ۱۰۰ زمان مختلف با روندهای افزایشی، ثابت و کاهشی نشان داده شده است.

روند سری زمانی

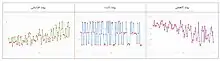
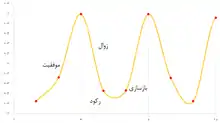
تناوب (Cyclic): تغییرات یکسان و تکراری در مقاطع میان‌مدت، تناوب در سری زمانی نامیده می‌شود. معمولا این تناوب ممکن است هر دو سال یا بیشتر اتفاق بیافتد. برای مثال تناوب در کسب و کار دارای یک چرخه چهار مرحله‌ای است که باعث می‌شود داده‌های مربوط به کسب و کار در یک دوره تناوب 3 ساله تکرار شوند.

تناوب در سری های زمانی

مثال‌ها
  • سری زمانی در اقتصاد، مانند قیمت سهام در روزهای متوالی، صادرات در ماه‌های متوالی، متوسط درآمد در ماه‌های متوالی …
  • سری زمانی فیزیک، بویژه در علوم مربوط به آثار جوی، علوم دریایی، فیزیک زمین (ژئو فیزیک).
  • سری‌های زمانی بازاریابی، تجزیه و تحلیل ارقام فروش در هفته یا ماه‌ها متوالی یک مسئلهٔ مهم در تجارت است.
  • سری‌های زمانی جمعیت نگاری، اندازه‌گیری سالانهٔ جمعیت با هدف پیش بینی تغییرات جمعیت در مدت زمان ده تا بیست سال آینده.
  • فرایندهای دوتایی، سری‌هایی که مشاهدات یکی از دو مقدار که معمولاً با ۰ و ۱ نشان می‌دهند را اختیار کند، که بخصوص در نظریه ارتباطات اتفاق می‌افتد را فرایند دوتایی می‌نامند.
  • فرایندهای نقطه ای، نوعی سری زمانی که پیشامدهای رخداده به طور تصادفی در زمان رخداده، زمان‌های رخ دادن تصادفات قطارها.

اصطلاحات
  • سری پیوسته، سری‌های که مشاهدات به طور پیوسته در زمان ایجاد می‌شوند (حتی اگر مقادیر گسسته‌ای اختیار کنند)
  • سری گسسته، سری که مشاهدات در زمان‌های معین و معمولاً در فاصله‌های مساوی رخ می‌دهند.

اهداف تجزیه وتحلیل سری‌های زمانی

می‌توان اهداف را به صورت زیر رده‌بندی کرد:

  • توصیف
  • تشریح
  • پیش بینی
  • کنترل
  • تطویل سری زمانی کوتاه مدت به بلند مدت(data generation)

هر کدام نیاز به تشریح دارد.

موضوعات مرتبط

منابع

    پانویس
    1. پیش بینی مصرف انرژی با سری‌های زمانی
    2. Energy Consumption Forecast by Time Series
    3. Production Line Halt, Prediction by Artificial Intelligence (Application of Artificial Neural Networks)
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.