رگرسیون خطی
رگرسیون خطی یا تنازل خطی یا وایازی خطی[persian-alpha 1] یکی از روشهای تحلیل رگرسیون است. رگرسیون یک نوع مدل آماریست برای پیشبینی یک متغیر از روی یک یا چند متغیر دیگر. رگرسیون خطی نوعی تابع پیشبینیکننده خطی است که در آن متغیر وابسته — متغیری که قرار است پیشبینی شود — به صورت ترکیبی خطی از متغیرهای مستقل پیشبینی میشود، بدین معنی که هر کدام از متغیرهای مستقل در ضریبی که در فرایند تخمین برای آن متغیر بهدست آمده ضرب میشود؛ جواب نهائی مجموع حاصلضربها به علاوه یک مقدار ثابت خواهد بود که آن هم در فرایند تخمین بهدست آمدهاست. سادهترین نوع رگرسیون خطی، رگرسیون خطی ساده است که بر خلاف رگرسیون خطی چندگانه، تنها یک متغیر مستقل دارد. نوع دیگر رگرسیون خطی رگرسیون خطی چندمتغیره است که در آن به جای پیشبینی یک متغیر وابسته چندین متغیر وابسته پیشبینی میشود.
| بخشی از مجموعه مباحث دربارهٔ آمار |
| تحلیل رگرسیون |
|---|
 |
| مدلها |
|
|
|
|
| تخمین |
|
|
|
|
| پیشزمینه |
|
|
فرایند تخمین سعی میکند ضرایبِ مدل رگرسیون خطی را به گونهای انتخاب کند که با دادههای موجود همخوانی داشته باشد، یعنی پیشبینیها به مقادیر رؤیت شده در دادهها نزدیک باشند و یکی از مهمترین مسائل در رگرسیون خطی، به حداقل رساندن اختلاف بین این دو است. راههای مختلفی برای حل این مسئله وجود دارد. در روشهای احتمالی، مدلهای رگرسیون خطی سعی در برآورد توزیع احتمال شرطیِ متغیر وابسته (و نه توزیع احتمال توأم) دارند که از آن طریق آمارهای از متغیر وابسته را به عنوان پیشبینی نهایی بهکار میبرند. از متداولترین آمارههای مورد استفاده میانگین است، اگر چه سایر آمارهها نظیر میانه یا چندکها نیز مورد استفاده قرار میگیرند.
یکی دیگر از روشهای متداول تخمین، روش کمترین مربعات است که در آن مجموع مربع تفاضل پیشبینیها و دادههای وابسته کمینه میشود. این روش مستلزم پیدا کردن وارونه ضرب خارجی ماتریس تمام دادههای مستقل با ماتریس ترانهادهٔ آن است، فرآیندی که میتواند به علت وارونهناپذیری ماتریس نهائی و کمبود داده پرهزینه و ناکارا باشد. از این رو عموماً از روشهای جایگزین مانند گرادیان کاهشی تصادفی استفاده میشود. با اینکه روش کمترین مربعات از متداولترین روشهای تخمین مدل رگرسیون خطی است اما روشهای دیگری مانند کمترین قدرمطلقها (که در آن مجموع قدرمطلق تفاضل پیشبینی و داده وابسته به عنوان تابع هزینه در نظرگرفته میشود) یا تخمین جریمه یافتهٔ کمترین مربعات (مانند جریمهٔ نُرمِ و جریمهٔ نُرمِ ) نیز مورد استفاده قرار میگیرد.
روش تخمین از طریق کمترین مربعات با روش تخمین میانگین از طریق اعمال برآورد درستنمایی بیشینه بر متغیر وابسته شرطی با در نظر گرفتن یک سری مفروضات معادل خواهد بود. این روش احتمالی برای محافظت مدل از بیشبرازش نیز مورد استفاده قرار میگیرد، به این شکل که در تخمین مدل، احتمال پسین به جای تابع درستنمایی بیشینه میشود و احتمال پیشین به پارامترهایی که نُرمِ کمتری دارند احتمال بالاتری اختصاص میدهد. در نتیجه مدل نهائی پارامترهایی را فراخواهد گرفت که بزرگ نیستند و این به نوبهٔ خود باعث حفاظت مدل از بیشبرازش میشود. روش استفادهٔ برآورد درستنمایی احتمال پسین معادل روش تخمین جریمه یافتهٔ کمترین مربعات است.
رگرسیون خطی بهطور گستردهای در علوم زیستی، رفتاری، اجتماعی، دارایی، اقتصاد و محیط زیست مورد استفاده قرار میگیرد. همچنین رگرسیون خطی و مشتقات آن یکی از ابزارهای شناخته شده و پرکاربرد در یادگیری ماشین هستند. با وجود کاربرد زیاد رگرسیون خطی در علوم مختلف، این روش محدودیتهایی هم دارد. بسیاری از مسائل پژوهشی در علوم اجتماعی در قالب مدلهای رگرسیون نمیگنجند و یک متغیر خروجی ندارند (مانند تجزیه و تحلیل خوشهای برای آشکار ساختن گروههای منسجم در دادهها). همچنین رگرسیون خطی برای پیدا کردن علّیت بین متغیرهای مستقل و وابسته ابزار مناسبی نیست.
مفاهیم
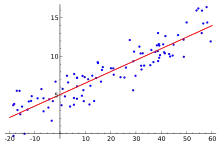
رگرسیون خطی یک مدل آماری برای پیشبینی یک یا چند متغیر از روی یک یا چند متغیر دیگر است. به متغیرهایی که پیشبینی بر روی آن انجام میشود متغیر وابسته و به متغیرهایی که پیشبینی به کمک آنها انجام میشود متغیرهای مستقل میگویند. متغیرهای وابسته را معمولاً با و متغیرهای مستقل را با نمایش میدهند. اگر تنها یک متغیر مستقل وجود داشته باشد مدل رگرسیون خطی را ساده و در غیر این صورت چندگانه مینامند. همچنین اگر به جای پیشبینی یک متغیر وابسته چندین متغیر وابسته پیشبینی شود، مدل رگرسیون خطی را چندمتغیره مینامند.[1] واژهٔ «رگرسیون» وامواژهای از زبان فرانسوی است و به معنی «برگشت» یا «پسگرایی» است؛ این واژه اولین بار توسط فرانسیس گالتون برای توصیف رابطهٔ خطی بین قد فرزندان و والدینشان مورد استفاده قرار گرفت. بهطور دقیقتر او از اصطلاح «برگشت (رگرسیون) به میانگین» برای توصیف این رابطه استفاده کرد.[2]
اگر فرض کنیم که تنها یک متغیر وابسته و چندین متغیر مستقل وجود داشته باشند، برای سهولت کار همهٔ متغیرهای مستقل را در یک بردار میگنجانیم.[3] اگر متغیر وابسته مقادیر عددی بگیرد مسئلهٔ مدلسازی «رگرسیون» نام میگیرد، و در غیر این حالت (یعنی وقتی متغیر وابسته رستهای باشد) به آن «دستهبندی آماری» گفته میشود.[4]
تاریخچه
استفاده از رگرسیون خطی از قرن نوزدهم میلادی شروع شد. اولین بار رگرسیون خطی در قالب کمترین مربعات و در کارهای آدرین ماری لژاندر[5] و کارل فریدریش گاوس ارائه شد.[6] این دو مستقل از یکدیگر و با استفاده از رگرسیون خطی، حرکت سیارات و ستارههای دنبالهدار را پیشبینی کردند.[7] گاوس بعدها نظریهٔ کمترین مربعات و قضیه گاوس-مارکوف را در سال ۱۸۲۱ منتشر کرد.[8] کارل پیرسون بعدتر روش گاوس را توسعه داد. او توزیع احتمال مشترک متغیر وابسته و متغیرهای مستقل را توزیع گاوسی فرض کرد.[9] رانلد فیشر اما بعد از او نشان داد که توزیع احتمال شرطی متغیر وابسته به شرط متغیرهای مستقل باید توزیع گاوسی باشد و نه توزیع احتمال مشترک آنها.[10][11]
استفاده از واژه رگرسیون به اواخر قرن نوزدهم بر میگردد.[2] در آن زمان فرانسیس گالتون برای پیدا کردن رابطهٔ قد فرزندان و والدین از روش رگرسیون استفاده کرد.[2] دادهها به او نشان دادند که والدین بلند قد معمولاً فرزندان کوتاهقدتری نسبت به خود دارند و بالعکس. او این رابطه را با یک خط نشان داد (که با یک شیب و یک عرض از مبدأ تعریف میشد). اگر چه این خط تمام دادهها را بر روی خود نمیگنجاند ولی میانگین قد فرزندان را بر حسب قد والدینی که قد یکسانی داشتند تخمین میزد.[2] اصطلاح رگرسیون در ابتدا فقط برای روش تخمین قد فرزندان از روی قد والدین به کار میرفت ولی به تدریج عمومیت پیدا کرد و برای تخمین میانگین یک متغیر وابسته با استفاده از ترکیب خطی چندین متغیر مستقل به کار برده شد.[2]
از لحاظ تاریخی رگرسیون خطی معمولاً از روش کمترین مربعات یا استنباط فراوانی گرایانه تخمین زده میشد ولی بعدها روشهای دیگری نیز مورد استفاده قرار گرفت.[12] کاربرد اولیهٔ رگرسیون خطی در علوم پایه و علوم تجربی بود و آدولف کوتله استفاده از این روش را در علوم اجتماعی متداول کرد و گسترش داد.[13]
در دهههای ۱۹۵۰ و ۱۹۶۰ اقتصاددانان از ماشینحساب الکترومکانیکی برای تخمین مدل رگرسیون خطی استفاده میکردند. قبل از دههٔ ۱۹۷۰، گاهی اوقات یک شبانهروز ساعت طول میکشد تا نتیجه یک رگرسیون دریافت شود.[14]
پیشفرضها
معمولاً چند پیشفرض برای استفاده از رگرسیون خطی در نظر گرفته میشود. اگر اختلاف بین متغیر وابسته و پیشبینی مدل را «خطا» یا «مانده» بنامیم، آنگاه مفروضات زیر باید در مدلسازی رگرسیون خطی برقرار باشند:[15]
- ماندهها از یک توزیع طبیعی پیروی میکنند.[15] این پیشفرض به این معنی است که توزیع مشروط متغیرهای وابسته یک توزیع طبیعی است. این پیشفرض برای کمترین مربعات ضروری است ولی در رگرسیون چندک یا رگرسیون میانه میتوان این پیش فرض را نقض کرد.
- ماندهها از هم مستقل هستند.[16] این پیشفرض متغیرهای مانده (و در نتیجه متغیرهای وابسته) را نسبت به هم مستقل میداند. برخی از روشها مانند کمترین مربعات تعمیم یافته قادر به کار با ماندههای همبسته هستند، گرچه بهطور معمول به دادههای بیشتری برای این کار نیاز هست، مگر اینکه از تنظیم مدل استفاده شود. رگرسیون خطی بیز یک روش کلی برای حل این مشکل است.
- واریانس ماندهها ثابت است.[16] این پیشفرض مقادیر ماندهها (و در نتیجه متغیرهای وابسته) را دارای واریانس ثابت میداند. در عمل، این فرض معمولاً نامعتبر است و ماندهها ناهمگن هستند. در رگرسیون چندک میتوان این فرض را نقض کرد.[17]
- بین متغیرهای مستقل همخطی وجود ندارد.[18] مفهوم این پیشفرض این است که ماتریس متغیرهای مستقل تمام رتبه باشد. اگر این شرط برقرار نباشد بعضی از متغیرهای مستقل ترکیبی خطی از یک یا چند متغیر خطی دیگر خواهند بود. تعداد کم داده میتواند این پیشفرض را نقض کند به خصوص زمانی که تعداد دادهها کمتر از تعداد پارامترهای مدل رگرسیون خطی (تعداد ضرایب رگرسیون خطی) باشد.
- رابطه بین میانگین متغیر وابسته و متغیرهای مستقل خطی است.[19] این پیشفرض بدان معنی است که میانگین متغیر وابسته، ترکیبی خطی از پارامترها (ضرایب رگرسیون) و متغیرهای مستقل است. این پیشفرض محدودیت زیادی ایجاد نمیکند زیرا خطی بودن فقط یک محدودیت برای پارامترها است. در رگرسیون خطی تعمیم یافته میتوان چندین متغیر جدید را از ترکیب متغیرهای مستقل ایجاد کرد، یا در رگرسیون چند جملهای ساده، متغیر وابسته را ترکیبی چند جملهای از متغیر مستقل در نظر گرفت. معمولاً برای جلوگیری از بیشبرازش و پیچیدگی مدلهای رگرسیون خطی تعمیم یافته نیاز به تنظیم مدل هست.
تخمین پارامترها
فرق رگرسیون خطی با سایر مدلهای رگرسیون در این است که در این مدل رابطهٔ بین متغیرهای مستقل و متغیر وابسته یک رابطهٔ خطی فرض میشود.[19] رگرسیون خطی، که خود نوعی تابع پیشبینیکنندهٔ خطی است، پیشبینی متغیر وابسته را از حاصلجمع ضرب متغیرهای مستقل در یک سری ضرایب بهدست میآورد. در رگرسیون خطی ساده که تنها یک متغیر مستقل وجود دارد، پیشبینی متغیر وابسته شکل یک خط مستقیم به خود میگیرد؛ در رگرسیون خطی با دو متغیر شکل پیشبینی یک صفحه خواهد بود، و در رگرسیون خطی با بیش از دو متغیر مستقل پیشبینی متغیر وابسته به صورت یک اَبَرصفحه خواهد بود.[20]
رگرسیون خطی ساده
رگرسیون خطی ساده میزان اثر یک متغیر مستقل بر یک متغیر وابسته را میسنجد و همبستگی رابطهٔ بین آنها را مورد سنجش قرار میدهد.[20]
مثلاً تحلیل رگرسیونی سادهٔ زیر با نقطه، متغیر مستقل و ضرایب و خطی است:
- خط راست:
در عبارت پیشین مقدار خطاست و پانویس شمارهٔ هر مشاهده (هر جفت و ) را نشان میدهد. با داشتن مجموعهای از این نقطهها میتوان مدل را به دست آورد:
عبارت «مانده» نام دارد و تخمینی است از اختلاف بین مقدار محاسبه شده و مقدار واقعی متغیر وابسته: . برای تخمین این مدل رگرسیون باید سه پارامتر تخمین زده بشوند: دو ضریب و و مانده (). روش رایج برای بهدستآوردن پارامترها، روش کمترین مربعات است. در این روش پارامترها را با کمینهکردن مجموع مربعات خطا به دست میآورند:
در مورد رگرسیون ساده، پارامترها با این روش برابر خواهند بود با:
که در آن و میانگین و هستند.
تفاوت رگرسیون و همبستگی
معمولاً زمانی میتوان از رگرسیون استفاده کرد که یک همبستگی بین متغیرهای مستقل و وابسته وجود داشته باشد. این همبستگی را میتوان به عنوان مثال از ضریب همبستگی پیرسن که عددی در بازه است بهدستآورد. ضریب همبستگی مثبت به این معنی است که با افزایش یک متغیر، متغیر دیگر هم افزایش مییابد و بالعکس، اما ضریب همبستگی منفی نشاندهنده رابطه معکوس بین دو متغیر است یعنی با افزایش یکی دیگری کاهش مییابد و بالعکس. ضریب صفر به این معنی است که هیچ رابطهای بین دو متغیر نیست و دو متغیر نسبت به هم مستقلند.[21]
هدف مدلهای همبستگی بررسی میزان رابطهٔ دو یا چند متغیر است. رگرسیون اما به دنبال پیشبینی یک یا چند متغیر براساس یک یا چند متغیر دیگر است. به بیان دیگر، همبستگی میزان و شدت رابطهٔ متغیرها را نشان میدهد اما رگرسیون معادلهای را برای پیشبینی متغیرها ارائه میکند.[19]
آنچه در خروجی نتایج رگرسیون و همبستگی باعث ایجاد تفاوت میشود آن است که در همبستگی همیشه اثرات متغیرها به صورت دو به دو مورد سنجش قرار میگیرد اما در یک مدل رگرسیون اثرات متغیرها به صورت همزمان بررسی میشود. یعنی در همبستگی رابطه متغیر با متغیر به وجود یا عدم وجود متغیر ارتباطی ندارد اما اما در رگرسیون تأثیر متغیر بر متغیر به وجود یا عدم وجود متغیر بستگی دارد (به شرط آن که متغیر هم در مدل رگرسیون به کار گرفته شود؛ چنین مدل رگرسیون خطی را «چندگانه» مینامند).
صورت مسئله
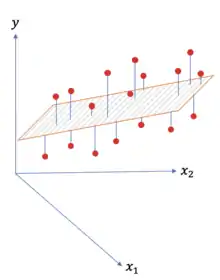
در بسیاری از مسائل رایج رگرسیون، ورودی چندمتغیره است.[22] اگر فرض کنیم متغیر ما بُعد دارد، یعنی ، مسئلهٔ رگرسیون به یک مسئلهٔ بهینهسازی برای پیدا کردن پارامتر تبدیل میشود، به این معنی که ما یک پارامتر چندمتغیره به اسم داریم و سعی میکنیم که متغیر وابسته که همان است را با بردار ، تخمین بزنیم که یعنی . حال اگر یک بعد دیگر به متغیر اضافه کنیم و مقدارش را همیشه عدد ثابت در نظر بگیریم () و را به صورتِ تغییر دهیم، تخمینی که از داریم در واقع ضرب نقطهای بردار ورودی و بردار پارامترهای ماست یعنی . حال فرض کنیم که تعداد مثالهایی که قرار است برای تخمین پارامترها استفاده کنیم است و این مثالها را به این شکل نمایش دهیم . در چنین مدلی پارامتر بهینه آن پارامتری است که یک تابع هزینه را به حداقل برساند و تخمینهای ما را به متغیر وابسته بسیار نزدیک کند. تابع هزینه را با جمع مربع تفاضل تخمینها با متغیر وابسته تعریف میکنیم، به این شکل که ، و با این حساب پارامتر بهینه عبارت است از:
کمترین مربعات
در این روش برای بهدست آوردن یا همان پارامتر بهینه، از تابع نسبت به گرادیان میگیریم و این گرادیان را برابر صفر قرار میدهیم و پارامتر بهینه را بهدست میآوریم.[23] از آنجا که تابع نسبت به تابعی کاملاً محدب است، در نقطهٔ کمینهٔ این تابع، گرادیان صفر خواهد بود و این روش پارامتر بهینه را بهدست میدهد.[24] برای تسهیل کار، شکل تابع را با بهکارگیری چند ماتریس ساده میکنیم. دو ماتریس برای این کار نیاز داریم: ماتریس و ماتریس . ماتریس ماتریس ورودیهای چندمتغیرهٔ ماست. در این ماتریس هر سطر معادل یک نمونه از دادهٔ ماست، مثلاً سطر ام برابر است با امین نمونه ورودی ما یعنی بردار ، از اینرو یک ماتریس خواهد بود. ماتریس از طرف دیگر برابر است با مجموعه متغیرهای وابسته در دادهٔ ما. سطر ام این ماتریس برابر است با متغیر وابسته برای امین نمونهٔ داده ما یا همان . ماتریس یک ماتریس است. با کمک این دو ماتریس میتوان تابع هزینه را به شکل ذیل تعریف کرد:
حال گرادیان این تابع را نسبت به پیدا میکنیم که میشود:
با برابر قرار دادن گرادیان با صفر پارامتر بهینه بهدست میآید:
در روش کمترین مربعات معمولاً برای جلوگیری از از بیشبرازش یا مقابله با مشکل عدم وارونپذیریِ از روش تنظیم تیخونوف[25][persian-alpha 2]، کمترین مربعات جزئی، یا رگرسیون مؤلفههای اصلی[26] استفاده میشود.
کمترین مربعات جزئی
کمترین مربعات جزئی یکی از روشهای جلوگیری از از بیشبرازش یا مقابله با مشکل عدم وارونپذیریِ است. این روش متناوباً مولفههایی متعامد ( در پایین) که ترکیبی خطی از مقادیر متغیرهای مستقل ( در پایین) هستند تولید میکند و در نهایت راه حل کمترین مربعات را بر روی این بردارها اعمال میکند. ضرایب این مولفهها با ضرب نقطهایِ مقادیر متغیرهای وابسته و مستقل برابر است. مقادیر متغیرهای مستقل در ابتدای کار استاندارد شدهاند به این معنی که میانگین صفر و واریانس یک دارند. در پایان هر مرحله مقادیر متغیرهای مستقل نسبت به مولفه آن مرحله متعامد میشوند. این کار باعث میشود که در پایان تمام مولفهها نسبت به هم متعامد باشند و ضریب رگرسیون مولفه با برابر باشد. الگوریتم تولید مولفهها برای به شکل پایین است ( از روش اعتبارسنجی متقابل محاسبه میشود):
از آنجا که یا همان مقدار پیشبینی شده، ترکیبی خطی از ها است و خود ها هم ترکیبی خطی از مقادیر متغیرهای مستقل هستند، در نهایت مدل رگرسیون ترکیبی خطی از مقادیر متغیرهای مستقل خواهد بود.[27]
گرادیان کاهشی تصادفی
روش پارامتر تخمین پارامتر بهینه از طریق کمترین مربعات ممکن است چند اشکال اساسی داشته باشد. یکی آنکه محاسبهٔ ممکن است زمانبر باشد. بُعدِ ماتریس مربعی برابر است با و اگر مقدار زیاد باشد زمان محاسبه معکوس این ماتریس میتواند مسئله ساز شود. به علاوه این ماتریس ممکن است اساساً معکوس پذیر نباشد. از این رو روشهای کاراتر و سریعتری برای تخمین پارامتر بهینه مورد استفاده قرار میگیرد. یکی از این روشها روش گرادیان کاهشی تصادفی است.[28] در این روش هر بار یک مثال را بهصورت اتفاقی از نمونههای داده انتخاب کرده، گرادیان تابع هزینه را حساب میکنیم و کمی در جهت خلاف گرادیان پارامتر را حرکت میدهیم تا به یک پارامتر جدید برسیم. گرادیان جهت موضعی بیشترین افزایش را در تابع به ما نشان میدهد، برای بیشترین کاهش موضعی در خلاف جهت گرادیان باید حرکت کرد. اینکار را آنقدر ادامه میدهیم که گرادیان به اندازه کافی به صفر نزدیک شود. بهجای اینکه دادهها را بهصورت تصادفی انتخاب کنیم میتوانیم به ترتیب داده شماره تا داده شماره را انتخاب کنیم و بعد دوباره به داده اولی برگردیم و این کار را چندین بار تکرار کنیم تا گرادیان تابع به اندازهٔ کافی به صفر نزدیک شود. از لحاظ ریاضی این کار را میتوان به شکل پایین انجام داد: پارامتر را در ابتدا بهصورت تصادفی مقدار دهی میکنیم و بعد برای داده ام و تمامی ها، یعنی از تا تغییر پایین را اعمال میکنیم، دراینجا همان مقداری است که در جهت گرادیان هربار حرکت میکنیم و مشتق جزئی داده ام در بُعد ام است:[28]
برآورد درستنمایی بیشینه
همچنان که پیشتر گفته شد، برای بهدست آوردن پارامتر بهینه میبایست تابع هزینه یعنی را به حداقل برسانیم. میتوان به همین پارامتر بهینه از روش برآورد درستنمایی بیشینه هم رسید. فرض میکنیم که متغیر وابسته یعنی یک متغیر تصادفی است که مقدارش از یک توزیع طبیعی (توزیع گاوسی) پیروی میکند. این توزیع احتمال، واریانس ثابتی به اسم دارد ولی میانگین آن ترکیبی خطی از متغیرهای مستقل یعنی است. به عبارت دیگر میانگین آن برابر است با . با احتساب میانگین و واریانس، توزیع متغیر وابسته عبارت است از . حال اگر فرض کنیم دادهها نسبت به یکدیگر مستقل هستند آن گاه تابع درستنمایی برای تمام دادهها میشود:[29]
حال باید به دنبال پارامتری باشیم که این تابع بزرگنمایی را بیشینه کند. از آنجا که تابع لگاریتم مطلقاً صعودیست، بهجای بیشینه کردن این تابع لگاریتمش را هم میشود بیشینه کرد و پارامتر بهینه را از آن طریق پیدا کرد:
پارامتر بهینه از این طریق برابر است با:
به این ترتیب پارامتری که را بیشینه میکند همان پارامتری است که را به حداقل میرساند. این یعنی در رگرسیون خطی نتیجهٔ روش کمترین مربعات با روش برآورد درستنمایی بیشینه یکی است.[30]
تنظیم مدل
پیچیدگی مدلهای پارامتری با تعداد پارامترهای مدل و مقادیر آنها سنجیده میشود. هرچه این پیچیدگی بیشتر باشد خطر بیشبرازش[persian-alpha 3] برای مدل بیشتر است.[31] پدیدهٔ بیشبرازش زمانی رخ میدهد که مدل بهجای یادگیری الگوهای موجود در داده، خود داده را به خاطر میسپارد. در این حالت، مدل برای آن مجموعه دادهٔ بهخصوص خوب عمل میکند اما برای دادههای مشابه دیگر عملکرد خوبی ندارد، که یعنی عمل یادگیری به خوبی انجام نشدهاست. برای جلوگیری از بیشبرازش در مدلهای خطی مانند رگرسیون خطی یا رگرسیون لجستیک، یک «جریمه»[persian-alpha 4] به تابع هزینه اضافه میشود تا از افزایش زیاد پارامترها جلوگیری شود. به این کار تنظیم مدل گفته میشود. دو راه متداول تنظیم مدلهای خطی روشهای و هستند.[32] در روش ضریبی از نُرمِ به تابع هزینه اضافه میشود و در روش ضریبی از نُرمِ که همان نُرمِ اقلیدسی است به تابع هزینهٔ اضافه میشود. نام روشهای و از نُرمی که در این روشها به تابع هزینه اضافه میشود گرفته شدهاست.[33]
در تنظیم مدل به روش تابع هزینه را به این شکل تغییر میدهیم:[32]
این روش تنظیم مدل که به روش لَسو[persian-alpha 5] نیز شهرت دارد باعث میشود که بسیاری از پارامترهای مدل نهائی صفر شوند و مدل به اصلاح خلوت[persian-alpha 6] شود.[34]
در تنظیم مدل به روش که به رگرسیون ستیغی[persian-alpha 7] نیز شهرت دارد تابع هزینه را به این شکل تغییر میدهیم:[32]
در روش تنظیم از طریق سعی میشود طول اقلیدسی بردار کوتاه نگه داشته شود. در هر دو روش و یک عدد مثبت است که میزان تنظیم مدل را معین میکند. هرچقدر کوچکتر باشد جریمهٔ کمتری برای بزرگی نرم بردار پارامترها یعنی محاسبه میشود. مقدار بهینهٔ از طریق آزمایش بر روی بخشی از دادهها پیدا میشود که در یادگیری مدل دخالت داده نشدهاند؛ به این بخش از دادهها، دادهٔ اعتبار[persian-alpha 8] یا مجموعهٔ اعتبارسنجی[persian-alpha 9] گفته میشود.[29]
با استفاده از ضرایب لاگرانژ میتوان اثبات کرد که تنظیم مدل و نوعی بهینهسازی مقید هستند. در تنظیم مدل تابع هزینه به نحوی کمینه میشود که نرمِ از یک مقدار مشخصی که بستگی به دارد بیشتر نشود. به همین نحو، تنظیم مدل تابع هزینه را همزمان با مقید کردن نرم کاهش میدهد.[33]
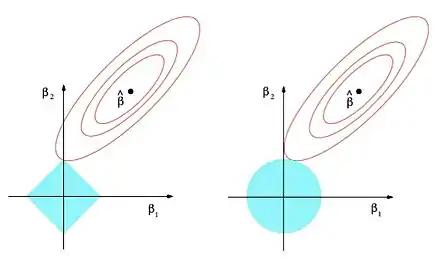
تفسیر احتمالی تنظیم مدل
اگر به جای روش برآورد درستنمایی بیشینه از روش بیشینهسازی احتمال پسین استفاده شود ساختار «تنظیم مدل» به دست میآید.[35] اگر مجموعهٔ داده را با و پارامتری که به دنبال تخمین آن هستیم را با نمایش بدهیم، طبق قانون بیز احتمال پسین یعنی متناسب خواهد بود با حاصلضرب درستنمایی یعنی و احتمال پیشین یعنی :[36]
از این رو:
معادلهٔ خط پیشین نشان میدهد که برای یافتن پارامتر بهینه فقط کافیست که احتمال پیشین را نیز در معادله دخیل کنیم. اگر احتمال پیشین را یک توزیع گاوسی با میانگین صفر و کوواریانس در نظر بگیریم به معادلهٔ پایین میرسیم:[36]
با ساده کردن این معادله به جواب زیر میرسیم که در آن برابر است با :
این جواب برابر با نتیجهٔ تنظیم مدل با نرم است.
بهطور مشابه، اگر احتمال پیشین را از نوع توزیع لاپلاس با میانگین صفر در نظر بگیریم به تنظیم مدل با نرم خواهیم رسید.[36]
انتخاب متغیر
معمولاً تعدادِ زیادِ متغیرهای مستقل، تعبیرپذیری مدلِ نهائی را دچار مشکل میکند. مضاف بر این بعضی از متغیرهای مستقل ممکن است باعث کاهش دقت مدل شوند. به همین دلیل حذف این متغیرها و استفاده از تنها یک زیرمجموعه بهینه از متغیرهای مستقل میتواند مدلی با کارایی بالاتری تولید کند.[27] روشهای مختلفی برای انتخاب متغیرها وجود دارد. یکی از سادهترین راهها محاسبه تابع هزینه به ازای تمام زیرمجموعههای ممکن و انتخاب زیرمجموعه بهینه با کمترین میزان هزینه است. در این روش مسئله رگرسیون خطی باید به ازای تمامی زیرمجموعهها، یعنی بار، حل شود. از اینرو این روش معمولاً برای مسائلی که دادههای زیادی دارند یا تعداد متغیرهای مستقل آن بزرگ است (معمولاً ) راه حل مناسبی نیست. روشهای پیشرو و پسرو که متناوباً متغیرهای مستقل را انتخاب یا حذف میکنند یا روشهای کوچک سازی که از طریق اعمال محدودیت بر روی پارامترها میزان تأثیرگذاری آنها را در مدل نهائی مهار میکنند، راههای بهتری برای انتخاب متغیر هستند.[27]
در روش پیشرو، ابتدا عرض از مبدأ از طریق محاسبه میانگین مقادیر متغیر وابسته بهدست میآید، سپس به تناوب در هر مرحله متغیری که باعث بیشترین کاهش تابع هزینه میشود به مدل افزوده میشود. به زبان دقیقتر در مرحله ، یک متغیر از متغیرهای مستقل که تا به حال انتخاب نشده به متغیر منتخب اضافه میشود. در نهایت بهترین زیرمجموعه از میانِ زیرمجموعهای که متناوباً ساخته شده با استفاده از اعتبارسنجی متقابل محاسبه میشود.[37] برای تسریع انتخاب متغیر مستقل بهینه در هر مرحله میتوان از تجزیه کیوآر استفاده کرد.[37] روش پسرو مانند روش پیشرو عمل میکند با این تفاوت که در ابتدا تمام متغیرهای مستقل مورد استفاده قرار میگیرند و در هر مرحله یک متغیر مستقل حذف میشود. بهترین متغیر برای حذف در هر مرحله متغیری است که کمترین امتیاز طبیعی را داشته باشد.[37]
در روشهای کوچک سازی که همان روشهای تنظیم مدل است، سعی بر این است که برای جلوگیری از بیشبرازش، میزان تأثیرگذاری پارامترها مهار شود. به همین منظور مسئله بهینهسازی به یک بهینهسازی مقید تغییر داده میشود تا نُرمِ یا از یک مقدار معینی زیادتر نشود. در روش کوچک سازی مسئله بهینهسازی به عبارت پایین تغییر شکل میدهد که معادل تنظیم مدل لسو است. این روش باعث میشود که مدل نهائی به اصطلاح خلوت شود و ضریب بسیاری از متغیرها صفر گردد.[38]
به صورت مشابه در روش کوچک سازی ، مسئله بهینهسازی با معادله پایین برابر خواهد بود که معادل رگرسیون ستیغی است. این روش باعث میشود که ضرایب رگرسیون زیاد بزرگ نشوند.[39]
تعمیم
رگرسیون چندک و میانه
رگرسیونهای خطی که بر کمترین مربعات استوارند، معمولاً سعی دارند که میانگین متغیر وابسته را بر اساس توزیع شرطی این متغیر و با کمک ترکیبی خطی از متغیرهای مستقل تخمین بزنند. در مقایسه، رگرسیون چندک[persian-alpha 10] هدف را بر محاسبه یک یا چند چندکِ متغیر وابسته میگذارد.[40] رگرسیون چندک معمولاً با دادههای پرت بهتر از رگرسیون معمولی کار میکند و پیشفرضهای کمتری دارد منجمله اینکه توزیع شرطی متغیر وابسته ضرورتاً لازم نیست توزیعی طبیعی باشد. همچنین رگرسیون چندک در مسائلی به کار میرود که هدف بدست آوردن توزیع مشروط متغیر وابسته باشد نه فقط یک آماره از آن مانند میانگین؛ چه که با استفاده از چندکهای یک توزیع میتوان کل توزیع را تقریب زد.[40] اگر تابع توزیع تجمعیِ متغیر باشد، و عددی در باشد، آنگاه چندک مرتبط با این عدد به این شکل تعریف میشود:[40]
میتوان نشانداد که:
که در اینجا است. حال اگر تابع توزیع تجمعی را نداشته باشیم و فقط نمونه از توزیع متغیر داشته باشیم آنگاه چندک متغیر را با بهینهسازی پایین میتوان بهدستآورد.[40]
حال اگر چندکِ متغیر وابسته را با ترکیبی خطی از متغیرهای مستقل تخمین بزنیم آنگاه هدف مسئله رگرسیون خطی پیدا کردن ضرایبی خواهد بود که دادههای وابسته را به چندکشان نزدیک کند:
این مسئله بهینهسازی با کمک برنامهریزی خطی حل میشود.
اگر با برابر باشد، رگرسیون خطی، میانه را تخمین خواهد زد و تابع هزینه به مجموع قدر مطلق تفاضل پیشبینی و داده وابسته تغییر شکل مییابد:
رگرسیون چندک در علوم بومشناسی کاربرد فراوانی دارد.[41] معمولاً به علت پیچیدگی و تعداد زیاد عوامل تأثیرگذار در یک رویداد طبیعی، توزیعهای شرطی متغیرهای وابسته اغلب واریانس بالا و غیر همسانی دارند که باعث میشود رابطه بین متغیرهای مستقل و میانگین توزیع شرطی ضعیف شود؛ تقریب کل توزیع شرطی با استفاده از تخمین خطی چندکهای توزیع شرطی حاوی اطلاعات بیشتری برای پژوهشگران این رشتهاست و این تقریب از طریق رگرسیون چندک به دست میآید.[41]
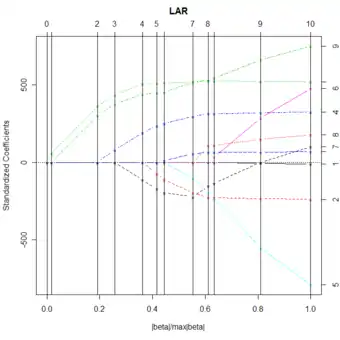
رگرسیون کمترین زاویه (لارس)
در رگرسیون کمترین زاویه که به آن رگرسیون لارس[persian-alpha 11] هم گفته میشود، ضرایب رگرسیون در یک فرایند افزایشی به شکل زیر تخمین زده میشوند:[43]
- در ابتدا تمام ضرایب با عدد صفر مقداردهی میشوند.
- متغیر مستقل که بیشترین ضریب همبستگی را با متغیر وابسته دارد انتخاب میشود.
- در جهت علامت ضریب همبستگی افزایش مییابد تا جایی که همبستگی متغیر دیگری مانند با مانده از همبستگی با مانده فزونی بیابد.
- حال (, ) در جهت بردار بهینهای که از کمترین مربعاتِ (, ) بهدست آمده افزایش داده میشود و همزمان ماندهها نیز محاسبه میشوند. متغیر دیگری پیدا میشود که همبستگی بیشتری با مانده متغیرهایی که تا به حال انتخاب شدهاند داشته باشد، و به جمع متغیرهایی انتخاب شده اضافه میشود و این روند تا انتخاب تمام متغیرها ادامه خواهد یافت.
رگرسیون لارس مانند رگرسیون لَسو باعث میشوند مدل نهائی خلوت شود و بسیاری از ضرایبِ مدل صفر شود. این مدل برای دادههایی بُعد بالا مورد استفاده قرار میگیرد.[42]
رگرسیون خطی با وزنهای موضعی
رگرسیون خطی با وزنهای موضعی[persian-alpha 12] همانند کمترین مربعات کار میکند با این تفاوت که مسئله پیشبینی برای هر کدام از دادههای جدید متفاوت خواهد بود. در رگرسیون خطی معمولی یک بار مدل تخمین زده میشود و بعد برای پیشبینی دادههای جدید از آن استفاده میشود. در مدل رگرسیون خطی با وزنهای موضعی اما برای هر داده جدید یک تخمین جدید رخ خواهد داد به گونهای که دادههای آموزشیِ نزدیکتر به داده جدید وزن بالاتری در مسئله بهینهسازی بگیرند و رگرسیون خطی به صورت موضعی انجام شود:[44]
در اینجا وزن موضعی داده جدید را با داده آموزشی نشان میدهد که با فاصله این دو داده نسبت به هم نسبت عکس دارد مانند نمونه پایین:
در این نوع رگرسیون دادههای آموزشی که به داده جدید نزدیکترند وزن بیشتری خواهند گرفت و دادههای دورتر عملاً نادیده گرفته میشوند.[44]
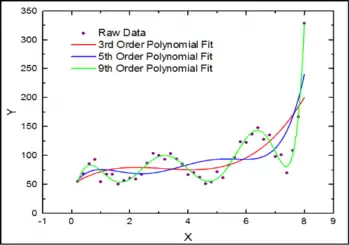
رگرسیون خطی تعمیمیافته
در رگرسیون خطی تعمیم یافته[persian-alpha 13] برای پیشبینی متغیر وابسته یک ترکیب خطی از نگاشتی از متغیرهای مستقل را در نظر میگیرند نه خود آن متغیرها را. به بیان دیگر:[45]
در این تابع، از فضای بُعدی به یک فضای بُعدی از طریق نگاشت منتقل شدهاست و سپس در آن فضا مقادیر جدید از طریق ترکیبی خطی با هم ترکیب شدهاند. به عنوان مثال در رگرسیون خطی ساده میتوان چندین متغیر جدید را از طریق یک چند جملهای درجه تولید کرد و سپس رگرسیون خطی را بوسیله آنها انجام داد، که این کار معادل نگاشت متغیر مستقل به یک فضای بعدی و انجام رگرسیون در آن فضاست:
رگرسیون خطی تعمیمیافته را میتوان زمانی به کار برد که رابطهٔ بین متغیر وابسته و مستقل یک خط راست نباشد اما بتوان از طریق یک انگاشت آن را به خطی راست تبدیل کرد.[45] به عنوان مثال برای پیشبینی میزان تنش در یک سازه ساختمانی از رگرسیون چند جملهای استفاده میکنند چه که رابطهٔ متغیر مستقل و وابسته خطی نیست و شباهت بیشتری به یک تابع درجه دو دارد.[46]
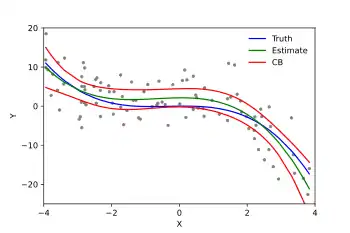
مدل سلسله مراتبی
مدل سلسله مراتبی[persian-alpha 14] (یا مدل چند سطحی[persian-alpha 15]) مدل رگرسیونی است که پارامترهای آن بر اساس خوشه یا سطحی که داده به آن تعلق دارد ممکن است تغییر کند.[47] به عنوان مثال در مسئله پیشبینی میزان سلامتی فرد از طریق مقدار درآمد او، از آنجا که افرادی که در یک محله زندگی میکنند میزان درآمد و سلامتی آنها به هم وابستگی بیشتری نسبت به بقیهٔ افراد دارد، بهتر است هر محله مدل رگرسیونِ جداگانه خود را داشته باشند.[47] در این مثال یک مدل رگرسیون خطی در سطح اول (سطح فرد در محله) ساخته میشود که بعضی یا همه پارامترهای آن میتواند برای هر محله متفاوت باشد. پارامترهای متفاوت میتواند خود از یک مدل رگرسیون دیگر در سطح دوم (سطح محلهها) یا بهصورت تصادفی تخمین زده شوند.[48]
اگر محلهٔ ، داده (فرد) داشته باشد، آنگاه برای این محله باید دو پارامتر و را پیدا کرد. برای داده () رابطه میان میزان درآمد فرد () و میزان سلامتی او () را به صورت پایین نشان میدهیم؛ در اینجا مقدار خطای تصادفی است که معمولاً از یک توزیع طبیعی پیروی میکند:
حال میتوان یا یا یا هر دو را برای هر محله متفاوت در نظر گرفت. این تفاوت میتواند تصادفی مدلسازی شود یا خود از یک مدل رگرسیون خطی دیگر که دارای یک یا چند متغیر مستقل در سطح دو (سطح محله) است برآورد شود. اگر فرض کنیم هر دوی و از یک مدل رگرسیون دیگر میآیند آنگاه میتوان به صورت پایین آنها را تخمین زد؛ در این دو معادله یک متغیر مستقل در سطح دو (سطح محله) است که به عنوان نمونه میتواند میزان ثروت محله باشد و و خطاهای تصادفی است.[48]
تجزیه و تحلیل مدل
از مدل رگرسیون خطی میتوان برای تحلیل رابطه متغیرهای مستقل با متغیر وابسته استفاده کرد. اگر یک متغیر مستقل مانند را در نظر بگیریم و بقیه متغیرهای مستقل را ثابت فرض کنیم، ضریب این متغیر یعنی ، میانگین تغییر در ازای تغییر یک واحد در را نشان میدهد که معادل میانگین مشتق جزئی نسبت به یا همان شیب خط رگرسیون با ثابت گرفتن سایر متغیرهای مستقل است. از این تأثیر با عنوان «تأثیر منحصر به فرد» بر روی نیز یاد میشود. از طرفی دیگر «تأثیر حاشیهای» بر روی از طریق رگرسیون خطی ساده (مدلی که فقط یک متغیر مستقل به اسم دارد) بهدست میآید.[49]
این امکان وجود دارد که با وجود تأثیر حاشیهای بزرگ، تأثیر منحصر به فرد متغیر تقریباً صفر باشد. این در شرایطی اتفاق خواهد افتاد که بعضی از متغیرهای مستقل دیگر بتوانند متغیر وابسته را به خوبی پیشبینی کنند و سهم در مقایسه با سایر متغیرها ناچیز باشد. از طرف دیگر، این امکان نیز وجود دارد که با وجود تأثیر حاشیهای تقریباً صفر، تأثیر منحصر به فرد بزرگ باشد. این اتفاق زمانی رخ میدهد که سایر متغیرها میزان زیادی از تغییر را توضیح میدهند و نقش نقشی تکمیلی است. در این حالت متغیر بخشی از را که توسط سایر متغیرها توضیحناپذیر است توضیح میدهد.[50]
معمولاً بعد از تخمین مدل رگرسیون، عیبیابی مدل رگرسیونی[persian-alpha 16] صورت میگیرد. در این عیبیابی معمولاً پیشفرضهای رگرسیون خطی مورد راستیآزمایی قرار میگیرند و دادههایی که تأثیر بیمورد در مدل نهائی داشتهاند شناسایی میشوند.[51] برای بررسی پیشفرضهای رگرسیون خطی از چندین نمودار و معیار استفاده میشود. از نمودار چندک-چندک میتوان برای مقایسه بین چندکهای ماندههای استاندارد شده و چندکهای توزیع طبیعی استاندارد و بررسی پیشفرض توزیع طبیعی ماندهها استفاده کرد. در صورت برقرار بودن پیشفرض، نمودار باید کم و بیش یک خط راست با زاویهٔ ۴۵ درجه نسبت به محورهای نمودار باشد. برای بررسی پیشفرض خطی بودن رابطه پارامترها و متغیر وابسته نموداری از ماندهها و مقادیر پیشبینی شده ترسیم میشود، اگر رابطه بین این دو گروه یک خط راست نباشد، پیشفرض نقض شدهاست. از این نمودار همچنین میتوان برای بررسی واریانسهمسانی ماندهها استفاده کرد. در نهایت برای پیدا کردن دادههایی که تأثیر بیمورد در مدل رگرسیون دارند از معیاری به اسم فاصله کوک[persian-alpha 17] استفاده میشود. این معیار تأثیر هر داده را بر ضرایب نهائی مدل رگرسیون -با تخمین یک مدل جدید بدون آن داده و مقایسه آن با مدل قبلی- میسنجد. دادههایی که فاصله کوک آنها از یک آستانه از پیش تعیین شده بیشتر است تأثیری منفی بر مدل رگرسیون دارند.[52]
کاربردها و محدودیتها
رگرسیون خطی بهطور گستردهای در علوم زیستی، رفتاری و اجتماعی[54] برای توصیف روابط احتمالی بین متغیرها مورد استفاده قرار میگیرد و از مهترین ابزارها برای این کار است.[54] رگرسیون خطی همچنین در قیمتگذاری داراییهای سرمایهای و تحلیل و اندازهگیری خطر سرمایهگذاری مورد استفاده قرار میگیرد. این مدل مستقیماً از ضریب بتا در مدل رگرسیون خطی به دست میآید که بازده سرمایه را به بازده تمام داراییها با ریسک بالا مربوط میکند.[55] همچنین در علم اقتصاد رگرسیون خطی یکی از مهمترین و پراستفادهترین ابزارهاست. به عنوان مثال، برای پیشبینی هزینه مصرف،[56] هزینه سرمایهگذاری ثابت، سرمایهگذاری موجودی، خرید صادرات کشور،[57] هزینه برای واردات،[57] تقاضا برای نگهداری داراییهای نقد،[58] تقاضای کار،[59] و عرضه نیروی کار[59] از این مدل استفاده میشود. در علوم محیط زیست نیز رگرسیون خطی کاربردهای گستردهای دارد. برای نمونه در کانادا، از رگرسیون خطی برای پیشبینی اثرات زیستمحیطی کارخانههای کاغذسازی و معادن فلزات بر روی ماهیها و مناطق دریابُن استفاده میکنند.[60] رگرسیون خطی در علم پزشکی نیز کاربرد دارد. به عنوان مثال اولین تحقیقاتی که رابطه استعمال دخانیات و مرگ و میر را نشان میداد از مدل رگرسیون خطی استفاده میکرد.[61][62] رگرسیون خطی در تخمین خط روند نیز کاربرد دارد.[63] خط روند، سیر تغییرات یک سری داده را در یک بازه زمانی طویلالمدت نشان میدهد. معمولاً به صورت چشمی سیر صعودی یا نزولی بودن این تغییرات را میتوان تشخیص داد ولی برای محاسبه دقیقتر شیب این تغییرات از رگرسیون خطی استفاده میشود. در مواردی که سیر تغییرات را با یک چندجملهای تخمین میزنند از رگرسیون خطی تعمیم یافته استفاده میکنند.[63] همچنین رگرسیون خطی و مشتقات آن یکی از ابزارهای شناخته شده و پرکاربرد در شاخههای هوش مصنوعی مخصوصاً در شاخه یادگیری ماشین است.[64]
گرچه رگرسیون خطی ابزاری بسیار انعطافپذیر برای تحقیقات علوم مختلف است، اما بدون محدودیت هم نیست. همه مسائل پژوهشی در قالب مدلهای رگرسیون نمیگنجد، به ویژه مسائلی که یک متغیر خروجی ندارند. به عنوان نمونه، تجزیه و تحلیل خوشهای یک ابزار آماری است که برای آشکار ساختن گروههای منسجم (یا خوشهها) در دادهها به کار میرود. رگرسیون مدل مناسبی برای کشف این نوع الگو در دادهها نیست.[12]
از آنجا که رگرسیون بر پیشینی متغیر خروجی (متغیر وابسته) متمرکز است، این شبهه ممکن است ایجاد شود که وجود رابطه بین متغیرهای مستقل و وابسته در مدل رگرسیون دال بر علیت این رابطه است. این نوع تعمیم نتایج مدل رگرسیونی نادرست است، و برای تحلیل علیت باید از روشهای آماری و تحقیقی دیگری بهره جست.[12]
در استفاده از مدل رگرسیون برای استنباط آماری نیز محدودیتهایی میتواند وجود داشته باشد. برای ارائهٔ استنباط معتبر، دادهها باید نمونهای تصادفی از یک جمعیت باشند یا در مطالعهٔ تجربی مورد نظر تصادفی شده باشند. بیشتر نمونهها در علوم اجتماعی این شرط را برآورده نمیکنند و استفاده از مدل رگرسیون برای تحلیل آنها خالی از اشکال نیست. البته، این یک انتقاد از خود رگرسیون نیست بلکه از طراحی مطالعات تجربی و محدودیتهای استنباط آماری با نمونهگیری غیر تصادفی است. با وجود همهٔ این محدودیتها، رگرسیون و مدلهای تعمیمیافتهٔ آن همچنان ابزاری فوقالعاده مفید برای پژوهشگران علوم مختلف محسوب میشوند.[12]
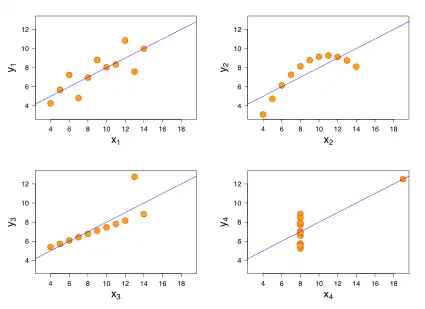
رگرسیون خطی برای بسیاری از مسائل مدل مناسبی نیست. این امکان وجود دارد که چندین مجموعه دادهٔ کاملاً متفاوت، مدل رگرسیون خطی یکسانی داشته باشند. چهارتایی آنسکوم نمونهٔ کلاسیک این حالت است. چهارتایی آنسکوم متشکل از چهار مجموعه دادهاست که نمودارهای کاملاً متفاوتی دارند ولی مدل رگرسیون خطی آنها کاملاً یکسان است. یک مجموعه در این مجموعهٔ چهارتایی (بالا سمت راست در شکل) دارای یک رابطهٔ کاملاً غیر خطی بین متغیرهاست. در یک مجموعه دیگر (پایین سمت چپ در شکل) با اینکه یک رابطهٔ خطی بین متغیرها حاکم است ولی به علت وجود یک دادهٔ پرت، مدل رگرسیون خطی به دست آمده نامناسب است. نهایتاً در یک مجموعه دیگر (پایین سمت راست در شکل) بین متغیرهای وابسته و مستقل هیچ همبستگی وجود ندارد ولی به علت وجود یک دادهٔ پرت، ضریب همبستگی این دو متغیر بالاست و یک مدل رگرسیون نامناسب برای پیشبینی متغیر وابسته تخمین زده شدهاست.[53]
جستارهای وابسته
یادداشتها
- معادلهای پیشنهادی برای عبارت انگلیسی linear regression
- Tikhonov regularization
- overfitting
- penalty
- LASSO مخفف least absolute shrinkage and selection operator
- sparse
- ridge regression
- validation data
- validation set
- quantile regression
- least-angle regression (LARS)
- locally weighted linear regression
- generalized linear regression
- hierarchical model
- multilevel model
- regression diagnostic
- Cook's distance
منابع
- Mardia, K. V; Kent, J. T.; Bibby, J. M. (1979). Multivariate Analysis. Academic Press. ISBN 0-12-471252-5.
- Galton, Francis (1886). "Regression Towards Mediocrity in Hereditary Stature". The Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583. Archived from the original on 4 August 2019. Retrieved 4 August 2019.
- David A. Freedman (2009). Statistical Models: Theory and Practice. Cambridge University Press. p. 26.
A simple regression equation has on the right hand side an intercept and an explanatory variable with a slope coefficient. A multiple regression equation has two or more explanatory variables on the right hand side, each with its own slope coefficient
- Bishop, C. M. (2006), Pattern Recognition and Machine Learning, Springer, p. 179, ISBN 978-0-387-31073-2
- A.M. Legendre. Nouvelles méthodes pour la détermination des orbites des comètes بایگانیشده در ۷ ژوئن ۲۰۱۹ توسط Wayback Machine, Firmin Didot, Paris, 1805. “Sur la Méthode des moindres quarrés” appears as an appendix.
- C.F. Gauss. Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum. (1809)
- Yan, Xin (2009), Linear Regression Analysis: Theory and Computing, World Scientific, pp. 1–2, ISBN 9789812834119, archived from the original on 8 June 2019, retrieved 25 September 2018,
Regression analysis … is probably one of the oldest topics in mathematical statistics dating back to about two hundred years ago. The earliest form of the linear regression was the least squares method, which was published by Legendre in 1805, and by Gauss in 1809 … Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the sun.
- C.F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae بایگانیشده در ۱۰ ژوئن ۲۰۱۹ توسط Wayback Machine. (1821/1823)
- Seal, Hilary L. (1967). "Studies in the History of Probability and Statistics. XV: The Historical Development of the Gauss Linear Model". Biometrika. 54 (1/2): 1–24. doi:10.2307/2333849. ISSN 0006-3444. Archived from the original on 24 January 2020. Retrieved 24 January 2020.
- Fisher, R.A. (1922). "The goodness of fit of regression formulae, and the distribution of regression coefficients". Journal of the Royal Statistical Society. 85 (4): 597–612. doi:10.2307/2341124. JSTOR 2341124. PMC 1084801.
- Aldrich, John (2005). "Fisher and Regression". Statistical Science. 20 (4): 401–417. ISSN 0883-4237. Archived from the original on 24 January 2020. Retrieved 24 January 2020.
- David C. Atkins. "Regression". www.encyclopedia.com. Archived from the original on 25 May 2019. Retrieved 2019-08-04.
- Stigler, Stephen M (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge: Harvard. ISBN 0-674-40340-1.
- Rodney Ramcharan. Regressions: Why Are Economists Obessessed with Them? بایگانیشده در ۵ اوت ۲۰۲۰ توسط Wayback Machine March 2006. Accessed 2011-12-03.
- Poole, Michael A.; O'Farrell, Patrick N. (1971). "The Assumptions of the Linear Regression Model". Transactions of the Institute of British Geographers (52): 145–158. doi:10.2307/621706. ISSN 0020-2754. Archived from the original on 24 May 2019. Retrieved 22 May 2019.
- Allen, R. G. D. (1939). "The Assumptions of Linear Regression". Economica. 6 (22): 191–201. doi:10.2307/2548931. ISSN 0013-0427. Archived from the original on 24 May 2019. Retrieved 22 May 2019.
- Koenker, Roger (2005). Quantile Regression. Cambridge University Press. pp. 147. ISBN 978-0-521-60827-5.
- Tibshirani, Robert (1996). "Regression Shrinkage and Selection via the Lasso". Journal of the Royal Statistical Society, Series B. 58 (1): 267–288. JSTOR 2346178.
- Hilary L. Seal (1967). "The historical development of the Gauss linear model". Biometrika. 54 (1/2): 1–24. doi:10.1093/biomet/54.1-2.1. JSTOR 2333849.
- Rencher, Alvin C.; Christensen, William F. (2012), "Chapter 10, Multivariate regression – Section 10.1, Introduction", Methods of Multivariate Analysis, Wiley Series in Probability and Statistics, 709 (3rd ed.), John Wiley & Sons, p. 19, ISBN 978-1-118-39167-9, archived from the original on 15 June 2019, retrieved 25 September 2018.
- Boddy, Richard; Smith, Gordon (2009). Statistical methods in practice: for scientists and technologists. Chichester, U.K.: Wiley. pp. 95–96. ISBN 978-0-470-74664-6.
- Rencher, Alvin C.; Christensen, William F. (2012-08-15). Methods of Multivariate Analysis (به English). John Wiley & Sons. p. 19. ISBN 9781118391679. Archived from the original on 5 October 2018.
- Yan, Xin (2009). Linear Regression Analysis: Theory and Computing. World Scientific. ISBN 9789812834119. Archived from the original on 5 October 2018.
- Rencher, Alvin C.; Christensen, William F. (2012-08-15). Methods of Multivariate Analysis (به English). John Wiley & Sons. p. 155. ISBN 9781118391679. Archived from the original on 5 October 2018.
- Golub, Gene H.; Hansen, Per Christian.; O'Leary, Dianne P. (1999-01-01). "Tikhonov Regularization and Total Least Squares". SIAM Journal on Matrix Analysis and Applications. 21 (1): 185–194. doi:10.1137/S0895479897326432. ISSN 0895-4798. Archived from the original on 10 September 2014. Retrieved 19 December 2019.
- Jolliffe, Ian T. (1982). "A note on the Use of Principal Components in Regression". Journal of the Royal Statistical Society, Series C. 31 (3): 300–303. doi:10.2307/2348005. JSTOR 2348005.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "The Elements of Statistical Learning". Springer Series in Statistics: 80–82. doi:10.1007/978-0-387-84858-7. ISSN 0172-7397. Archived from the original on 27 December 2019. Retrieved 30 December 2019.
- Zhang, Tong (2004). "Solving Large Scale Linear Prediction Problems Using Stochastic Gradient Descent Algorithms". Proceedings of the Twenty-first International Conference on Machine Learning. ICML '04. New York, NY, USA: ACM: 116–. doi:10.1145/1015330.1015332. ISBN 978-1-58113-838-2. Archived from the original on 7 October 2008. Retrieved 17 May 2019.
- Machine learning: a probabilistic perspective بایگانیشده در ۴ نوامبر ۲۰۱۸ توسط Wayback Machine, Kevin P Murphy, 2012, p. 225, Cambridge, MA
- Machine learning: a probabilistic perspective بایگانیشده در ۴ نوامبر ۲۰۱۸ توسط Wayback Machine, Kevin P Murphy, 2012, p. 217, Cambridge, MA
- Bühlmann, Peter; van de Geer, Sara (2011). "Statistics for High-Dimensional Data". Springer Series in Statistics. doi:10.1007/978-3-642-20192-9. ISSN 0172-7397. Archived from the original on 21 February 2019. Retrieved 5 October 2018.
- Bühlmann, Peter; van de Geer, Sara (2011). Theory for ℓ1/ℓ2-penalty procedures. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 249–291. doi:10.1007/978-3-642-20192-9_8. ISBN 9783642201912. Archived from the original on 5 October 2018.
- Bishop, C. M. (2006), Pattern Recognition and Machine Learning, Springer, p. 146, ISBN 978-0-387-31073-2
- Natarajan, B. K. (1995). "Sparse Approximate Solutions to Linear Systems". SIAM Journal on Computing. 24 (2): 227–234. doi:10.1137/s0097539792240406. ISSN 0097-5397. Archived from the original on 24 May 2019. Retrieved 5 October 2018.
- Bishop, Christopher M (2016-08-23). Pattern Recognition and Machine Learning (به English). New York: Springer New York. p. 30. ISBN 9781493938438. Archived from the original on 5 October 2018.
- Robert, Christian (2014-04-03). "Machine Learning, a Probabilistic Perspective". CHANCE. 27 (2): 62–63. doi:10.1080/09332480.2014.914768. ISSN 0933-2480. Archived from the original on 8 April 2019. Retrieved 15 November 2018.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "The Elements of Statistical Learning". Springer Series in Statistics: 58. doi:10.1007/978-0-387-84858-7. ISSN 0172-7397. Archived from the original on 27 December 2019. Retrieved 30 December 2019.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "The Elements of Statistical Learning". Springer Series in Statistics: 68–69. doi:10.1007/978-0-387-84858-7. ISSN 0172-7397. Archived from the original on 27 December 2019. Retrieved 30 December 2019.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "The Elements of Statistical Learning". Springer Series in Statistics: 61–64. doi:10.1007/978-0-387-84858-7. ISSN 0172-7397. Archived from the original on 27 December 2019. Retrieved 30 December 2019.
- Koenker, Roger (2005). Quantile Regression. Cambridge University Press. ISBN 978-0-521-60827-5.
- Cade, Brian S.; Noon, Barry R. (2003). "A gentle introduction to quantile regression for ecologists" (PDF). Frontiers in Ecology and the Environment. 1 (8): 412–420. doi:10.2307/3868138. JSTOR 3868138. Archived (PDF) from the original on 7 January 2019. Retrieved 17 August 2019.
- Fraley, Chris; Meier, Lukas; Choi, Nam Hee; Hesterberg, Tim (2008). "Least angle and ℓ1 penalized regression: A review". Statistics Surveys. 2: 61–93. doi:10.1214/08-SS035. ISSN 1935-7516. Archived from the original on 29 March 2019. Retrieved 17 August 2019.
- Efron, Bradley; Hastie, Trevor; Johnstone, Iain; Tibshirani, Robert (2004). "Least Angle Regression" (PDF). Annals of Statistics. 32 (2): pp. 407&ndash, 499. arXiv:math/0406456. doi:10.1214/009053604000000067. MR 2060166. Archived (PDF) from the original on 19 June 2018. Retrieved 4 August 2019.
- Cleveland, William S.; Devlin, Susan J. (1988-09-01). "Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting". Journal of the American Statistical Association. 83 (403): 596–610. doi:10.1080/01621459.1988.10478639. ISSN 0162-1459. Archived from the original on 22 May 2019. Retrieved 4 August 2019.
- Goldberger, Arthur S. (1962-06-01). "Best Linear Unbiased Prediction in the Generalized Linear Regression Model". Journal of the American Statistical Association. 57 (298): 369–375. doi:10.1080/01621459.1962.10480665. ISSN 0162-1459. Archived from the original on 18 February 2021. Retrieved 4 August 2019.
- "(PDF) Application of polynomial regression models for prediction of stress state in structural elements". ResearchGate. Archived from the original on 18 February 2021. Retrieved 2019-08-17.
- Bryk, Stephen W. Raudenbush, Anthony S. (2002). Hierarchical linear models: applications and data analysis methods (2. ed. , [3. Dr.] ed.). Thousand Oaks, CA [u.a.]: Sage Publications. ISBN 978-0-7619-1904-9.
- Fidell, Barbara G. Tabachnick, Linda S. (2007). Using multivariate statistics (5th ed.). Boston ; Montreal: Pearson/A & B. ISBN 978-0-205-45938-4.
- Warne, Russell T. (2011). "Beyond multiple regression: Using commonality analysis to better understand R2 results". Gifted Child Quarterly. 55 (4): 313–318. doi:10.1177/0016986211422217.
- Berk, Richard A. (2007). "Regression Analysis: A Constructive Critique". Criminal Justice Review. 32 (3): 301–302. doi:10.1177/0734016807304871.
- Everitt, B.S. (2002) The Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-X (entry for Regression diagnostics)
- Cook, R. Dennis (February 1977). "Detection of Influential Observations in Linear Regression". Technometrics. American Statistical Association. 19 (1): 15–18. doi:10.2307/1268249. JSTOR 1268249. MR 0436478.
- Anscombe, F. J. (1973). "Graphs in Statistical Analysis". American Statistician. 27 (1): 17–21. doi:10.1080/00031305.1973.10478966. JSTOR 2682899.
- Dodhia, Rahul M. (2005). "Review of Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences". Journal of Educational and Behavioral Statistics. 30 (2): 227–229. ISSN 1076-9986. Archived from the original on 24 May 2019. Retrieved 21 May 2019.
- Cook, Douglas O.; Kieschnick, Robert; McCullough, B. D. (2008-12-01). "Regression analysis of proportions in finance with self selection". Journal of Empirical Finance. 15 (5): 860–867. doi:10.1016/j.jempfin.2008.02.001. ISSN 0927-5398. Archived from the original on 24 May 2019. Retrieved 21 May 2019.
- Deaton, Angus (1992). Understanding Consumption. Oxford University Press. ISBN 978-0-19-828824-4.
- Krugman, Paul R.; Obstfeld, M.; Melitz, Marc J. (2012). International Economics: Theory and Policy (9th global ed.). Harlow: Pearson. ISBN 978-0-273-75409-1.
- Laidler, David E. W. (1993). The Demand for Money: Theories, Evidence, and Problems (4th ed.). New York: Harper Collins. ISBN 978-0-06-501098-5.
- Ehrenberg; Smith (2008). Modern Labor Economics (10th international ed.). London: Addison-Wesley. ISBN 978-0-321-53896-3.
- EEMP webpage بایگانیشده در ۲۰۱۱-۰۶-۱۱ توسط Wayback Machine
- Doll, R. , Wheatley, K. , Gray, R. et al. "Mortality in relation to smoking: 40 years' observations on male British doctors ." BMJ 1994;309:901-911 (8 de octubre).
- "Environmental Tobacco Smoke and Adult Asthma" بایگانیشده در ۲۱ فوریه ۲۰۰۹ توسط Wayback Machine Division of Pulmonary and Critical Care Medicine, Division of Occupational and Environmental Medicine; Department of Medicine, Institute for Health Policy Studies; and Department of Epidemiology and Biostatistics, Universidad de California, San Francisco, California. (en inglés)
- Utilización de las líneas de tendencia, Paritech (en inglés)
- "Linear Regression (Machine Learning)" (PDF). University of Pittsburgh. Archived (PDF) from the original on 2 February 2017. Retrieved 21 May 2019.
برای مطالعهٔ بیشتر
- سنفورد وایزبرگ (۱۳۷۴). رگرسیون خطی کاربردی. ترجمهٔ حسینعلی نیرومند. دانشگاه فردوسی مشهد. شابک ۹۷۸۹۶۴۶۳۳۵۱۹۶.
- عبدالرضا بازرگانلاری (۱۳۸۵). رگرسیون خطی کاربردی. دانشگاه شیراز. شابک ۹۶۴۴۶۲۳۷۴۶.
- تقی اخوان نیاکی، مجید خدمتی (۱۳۹۴). تجزیه و تحلیل رگرسیون. دانشگاه صنعتی شریف، مؤسسه انتشارات علمی. شابک ۹۷۸۹۶۴۲۰۸۱۲۵۷.
- داگلاس مونتگمری، الیزابت پک (۱۳۹۰). مقدمه ای بر تحلیل رگرسیون خطی. ترجمهٔ ابراهیم رضوی پاریزی. دانشگاه شهید باهنر کرمان. شابک ۹۷۸-۹۶۴-۲۵۰۰-۲۹-۱.
- ویلیام وی (۱۳۹۰). تحلیل سریهای زمانی: روشهای یک متغیری و چند متغیری. ترجمهٔ حسینعلی نیرومند. دانشگاه فردوسی مشهد. شابک ۹۶۴۶۳۳۵۱۹۵.