شبکه‌های بیزی

یک شبکهٔ بیزی یا «شبکه باور» یا «شبکه باور بیزی» (به انگلیسی: Bayesian network) یک گراف سودار غیرمدور است که مجموعه‌ای از متغیرهای تصادفی و نحوه ارتباط مستقل آن‌ها را نشان می‌دهد. به عنوان نمونه یک شبکه بیزی می‌تواند نشان دهنده ارتباط بین بیماری‌ها و علائم آن‌ها باشد. پس با داشتن علائم باید بتوان احتمال یک بیماری خاص را در یک بیمار تشخیص داد.

یک شبکه بیزی

شبکه بیزین یک ابزار نسبتاً جدید برای شناسایی (هویت) روابط احتمالی به منظور پیشگویی یا ارزیابی کلاس عضویت است.[1]

به‌طور خلاصه می‌توان گفت شبکه بیزین، نمایش بامعنی روابط نامشخص ما بین پارامترها در یک حوزه می‌باشد. شبکه بیزین گراف جهت دار غیر حلقوی از نودها برای نمایش متغیرهای تصادفی و کمانها برای نمایش روابط احتمالی مابین متغیرها به‌شمار می‌رود.

خصوصیات

شبکه‌های بیزی در زمینه استدلال احتمالی به‌طور گسترده مورد استفاده قرار می‌گیرند و به درخت متصل بر روی احتمالات استدلال شده تبدیل می‌شوند. شبکه‌های بیزین به تجزیه زیرگراف اصلی ماکزیمم درخت متصل تبدیل می‌شوند و بیشتر از درخت‌های متصل کاربرد دارند. شبکه بیزین عموماً به صورت آشکار با مقادیر اولیه قابل قبول و روابط ما بین متغیرها توزیع می‌شود. در مسائل دنیای واقعی بسیار کاربرد دارند. در چندین سال پیش شبکه‌های بیزین توسط افراد مورد توجه قرار گرفتند و به عنوان گروه‌های زیست‌شناسی در روش‌های شبکه‌های ژنی توسط افرادی به کار گرفته شدند. شبکه بیزین یک مدل گرافیکی برای نمایش احتمالات مابین متغیرهای موردنظر می‌باشد. از طرفی شبکه‌های بیزین روشی برای نمایش توزیع احتمالی پیوسته بزرگ به صورت نمایی و روش فشرده می‌باشند که اجازه محاسبات احتمالی به‌طور مؤثر را می‌دهند. آن‌ها از ساختار مدل گرافیکی برای ضوابط مستقل مابین متغیرهای تصادفی استفاده می‌کنند. شبکه‌های بیزین اغلب برای شرایط مدل احتمالی استفاده می‌شوند و به استدلالهای تحت شرایط نامشخص (احتمالی، عدم قطعیت) کمک می‌کنند. این شبکه شامل بخش کیفی (مدل ساختاری) است که نمایش بصری از فعل و انفعالات در میان متغیرها و بخش کمی (مجموعه‌ای از مشخصات احتمال محلی) را فراهم می‌کند، که مجاز به استنتاج احتمالات و اندازه‌گیری عددی است که متغیرها یا مجموعه‌ای از متغیرها را تحت تأثیر قرار می‌دهد. بخش کیفی به صورت توزیع احتمالی پیوسته که منحصربه‌فرد می‌باشد بر روی کلیه متغیرها تعریف می‌شود.

جملات مستقل

فقدان لبه‌ها در شبکه بیزین نشانگر جملات مستقل از هم می‌باشد. رمزگذاری شبکه بیزین مطابق با جملات مستقل در هر متغیر تصادفی است. یک متغیر مستقل به صورت صعودی وضعیت والدین شبکه را نشان می‌دهد. همچنین شبکه بیزین برای نمایش توزیع احتمالی ویژه و اتصال توزیع بر روی همه متغیرها به صورت نودها در گراف نمایش داده می‌شود. این توزیع با یک مجموعه از جدول احتمال شرطی مشخص می‌شود. هر نود به جدول احتمال شرطی منتسب شده و توسط اطلاعات احتمالی کمی مشخص می‌گردد. همانند جدولی احتمالات در وضعیت ممکن از نود در ترکیب ممکن از والدینش مشخص می‌گردد. برای نودهای بدون والد احتمالات بر روی نودهای دیگر بدون قید و شرط می‌باشند که این نودها احتمالات اولیه بر روی متغیرها نامیده می‌شوند.

ساختار

به عبارت دیگر یک شبکه بیزین گراف جهت دار غیر حلقوی است و شامل موارد زیر می‌باشد:

1. گره ها (دوایر کوچک): برای نمایش متغیرهای تصادفی
2. کمانها (پیکانهای نوک تیز) برای نمایش روابط احتمالی ما بین متغیرها

برای هر نود توزیع احتمال محلی وجود دارد که به نود وابسته‌است و از وضعیت والدین مستقل می‌باشد.[1]

مثال

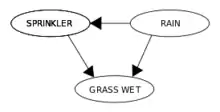
دو رویداد می‌تواند باعث مرطوب شدن چمن شود: یک آبپاش فعال یا باران. باران تأثیر مستقیمی در استفاده از آب پاش دارد (یعنی وقتی باران می‌بارد، آبپاش معمولاً فعال نیست). این وضعیت را می‌توان با یک شبکه بیزی مدل‌سازی کرد (در سمت راست نشان داده شده). هر متغیر دارای دو مقدار ممکن است T (برای true) و F (برای false).

یک شبکه ساده بیزی با جداول احتمالات شرطی

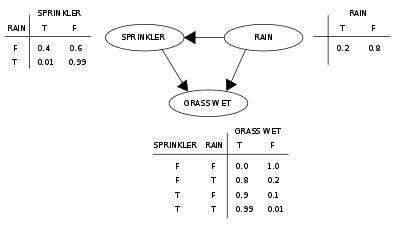
دو رویداد می‌تواند باعث مرطوب شدن چمن شود: یک آبپاش فعال یا باران. باران تأثیر مستقیمی در استفاده از آب پاش دارد (یعنی وقتی باران می‌بارد، آبپاش معمولاً فعال نیست). این وضعیت را می‌توان با یک شبکه بیزی مدل‌سازی کرد (در سمت راست نشان داده شده). هر متغیر دارای دو مقدار ممکن است T (برای true) و F (برای false).

تابع احتمال مشترک:

${\displaystyle \Pr(G,S,R)=\Pr(G\mid S,R)\Pr(S\mid R)\Pr(R)}$

به طوریکه

G = "Grass wet (true/false)", S = "Sprinkler turned on (true/false)", and R = "Raining (true/false)".

این مدل می‌تواند با توجه به وجود معلولی (اصطلاحاً معکوس) مانند "احتمال باران آمدن با توجه به مرطوب بودن علف چقدر است؟" به سوالات مربوط به وجود علت پاسخ دهد. با استفاده از فرمول احتمال شرطی و جمع‌بندی تمام متغیرهای مزاحم:

${\displaystyle \Pr(R=T\mid G=T)={\frac {\Pr(G=T,R=T)}{\Pr(G=T)}}={\frac {\sum _{S\in \{T,F\}}\Pr(G=T,S,R=T)}{\sum _{S,R\in \{T,F\}}\Pr(G=T,S,R)}}}$

با استفاده از بسط تابع احتمال مشترک ${\displaystyle \Pr(G,S,R)}$ و احتمالات مشروط از جداول احتمال شرطی (CPT) که در نمودار بیان شده‌است، می‌توان هر عبارت را در مجموع‌های موجود در صورت و مخرج را ارزیابی کرد. مثلاً،

${\displaystyle {\begin{aligned}\Pr(G=T,S=T,R=T)&=\Pr(G=T\mid S=T,R=T)\Pr(S=T\mid R=T)\Pr(R=T)\\&=0.99\times 0.01\times 0.2\\&=0.00198.\end{aligned}}}$

سپس نتایج عددی (مشتق شده توسط مقادیر متغیر مرتبط) چنین هستند

${\displaystyle \Pr(R=T\mid G=T)={\frac {0.00198_{TTT}+0.1584_{TFT}}{0.00198_{TTT}+0.288_{TTF}+0.1584_{TFT}+0.0_{TFF}}}={\frac {891}{2491}}\approx 35.77\%.}$

منابع

1. ((بررسی روشهای مربوط به شبکه‌های بیزین و کاربردهای آن

Timo Koski, John M. Noble, Bayesian Networks An Introduction.