گرادیان کاهشی تصادفی

[1]گرادیان کاهشی تصادفی (به انگلیسی: (Stochastic Gradient (SGD) روشی مبتنی بر تکرار برای بهینه‌سازی یک تابع مشتق‌پذیر به نام تابع هدف (تابع هزینه) است که یک تقریب تصادفی از روش گرادیان کاهشی می‌باشد. در حقیقت گرادیان کاهشی تصادفی الگوریتمی در اختیار ما قرار می‌دهد که طی چند حلقهٔ تکرار مقدار کمینه یک تابع و مقادیری را که با ازای آن‌ها تابع کمینه مقدار خود را می‌گیرد، بدست بیاوریم. به تازگی مقاله‌ای[2] ابداع این روش را به هربرت رابینز و ساتِن مونرو (به انگلیسی: Herbert Robins and Sutton Monro) برای انتشار مقاله‌ای در باب گرادیان کاهشی تصادفی در سال ۱۹۵۱ نسبت داده‌است. تفاوت گرادیان کاهشی تصادفی با گرادیان کاهشی استاندارد در این است که برخلاف گرادیان کاهشی استاندارد که برای بهینه‌سازی تابع هدف از تمام داده‌های آموزشی استفاده می‌کند، گرادیان کاهشی تصادفی از گروهی از داده‌های آموزشی که به‌طور تصادفی انتخاب می‌شود برای بهینه‌سازی استفاده می‌کند. این روش در مسائل آماری و یادگیری ماشین کاربرد فراوانی دارد.

پیشینه

در برآوردهای آماری و یادگیری ماشین معمولاً مسائلی به‌وجود می‌آید که در آن‌ها نیاز است تابعی مانند ${\displaystyle {\mathcal {f}}}$از داده‌های آماری با یک یا چند پارامتر (به شکل ضریب یا اشکال دیگر) تعریف کنیم و سپس این پارامترها را طوری مشخص کنیم که مجموع (یا میانگین) مقادیر تابع ${\displaystyle {\mathcal {f}}}$به ازای تک تک داده‌های آماری، حداقل مقدار ممکن خود بشود. فرض کنید مجموعه‌ای از داده‌های آماری داریم و تابع ${\displaystyle {\mathcal {f}}}$را برای این داده‌ها فقط بر حسب یک پارامتر ${\displaystyle \theta }$ تعریف کرده‌ایم، در این صورت با دادن داده ${\displaystyle {\boldsymbol {i}}}$ام از مجموعهٔ داده‌ها به تابع ${\displaystyle {\mathcal {f}}}$ یک تابع از ${\displaystyle \theta }$ بدست می‌آوریم که آن را ${\displaystyle {\mathcal {J}}_{\boldsymbol {i}}({\boldsymbol {\theta }})}$ می‌نامیم. حال مسئله به پیدا کردن ${\displaystyle \theta }$ ای که عبارت زیر را کمینه می‌کند، ساده می‌شود:

${\displaystyle {\mathcal {J}}({\boldsymbol {\theta }})=\left({\frac {1}{n}}\right)\textstyle \sum _{{\boldsymbol {i}}=1}^{n}\displaystyle {\mathcal {J}}_{\displaystyle i}({\boldsymbol {\theta }})}$

یا به عبارت دیگر:

${\displaystyle {\mathcal {J}}({\boldsymbol {\theta }})={E}[\displaystyle {\mathcal {J}}_{\displaystyle i}({\boldsymbol {\theta }})]}$

که ${\displaystyle {\mathcal {J}}({\boldsymbol {\theta }})}$ همان تابع هدف یا تابع هزینه است.

برای حل چنین مسئله‌ای از گرادیان کاهشی استاندارد یا در مواردی از گرادیان کاهشی تصادفی استفاده می‌شود. در آمار کلاسیک زمینه‌هایی مثل کمترین مربعات یا برآورد درست‌نمایی بیشینه، مسائلی مشابه در باب کمینه‌سازی مجموع جملات مطرح می‌شود. همچنین مسئلهٔ مینیمم‌سازی جمع جملات در اصل کمینه‌سازی خطر تجربی (Empirical risk minimization) نیز مطرح می‌شود.

در بسیاری از موارد تابع هدف تابعی ساده می‌شود که اعمال روش گرادیان کاهشی روی آن پیچیده و زمان‌بر نیست در این موارد از روش گرادیان کاهشی استاندارد استفاده می‌شود، مانند خانوادهٔ توابع نمایی یک پارامتره که در ارزیابی توابع اقتصادی استفاده می‌شود. اما از آنجا که در روش گرادیان کاهشی استاندارد یا تصادفی به محاسبهٔ گرادیان تابع هدف در هر حلقه نیاز است، در بعضی از موارد که پارامترهای تابع هدف زیاد اند یا مجموعهٔ داده‌های آموزشی بسیار بزرگ است محاسبهٔ انجام شده در هر حلقه می‌تواند بسیار زمان‌بر و پیچیده باشد به همین دلیل در این موارد از گرادیان کاهشی تصادفی استفاده می‌شود که در هر حلقه این عملیات را تنها برای بخشی از مجموعهٔ داده‌های آموزشی که در اختیار داریم، انجام می‌دهد. در روش گرادیان کاهشی تصادفی در هر حلقه عملیات موردنظر بر روی تنها یک عضو مجموعهٔ داده‌های آموزشی که در هر حلقه یه‌صورت تصادفی انتخاب می‌شود انجام نمی‌شود و در عوض بر روی زیرمجموعه‌ای از آن انجام می‌شود؛ این امر دو دلیل دارد:[3]

• پراکندگی مقدار بدست آمده برای پارامتر را در هر حلقه کم می‌کند و همگرایی پایدارتر پیش می‌رود.
• بهره‌گیری از عملیات ماتریسی که پیاده‌سازی بسیار سریعی دارد.

کاربردها

گرادیان کاهشی تصادفی یک الگوریتم محبوب و متداول برای یادگیری طیف گسترده‌ای از مدل‌ها در یادگیری ماشین است، از جمله ماشین‌های بردار پشتیبانی، رگرسیون لجستیک و مدل‌های گرافیکی.[4] الگوریتم بازگشت به عقب که عملاً الگوریتم استاندارد برای یادگیری شبکه‌های عصبی مصنوعی است در واقع روشی برای پیدا کردن گرادیان شبکه برای استفاده در گرادیان کاهشی تصادفی است.[5] گرادیان کاهشی تصادفی در جامعه ژئوفیزیک نیز کاربردهایی دارد مانند مسئله وارونگی کامل شکل‌موج (FWI).[6]

روش پیاده‌سازی

در پیاده‌سازی کلی گرادیان کاهشی تصادفی ابتدا بردار پارامترها که برداری است که شامل تمام پارامترهای تابع هزینه است را ${\displaystyle \theta }$ می‌نامیم. ${\displaystyle \theta }$ را برابر برداری دلخواه قرار می‌دهیم سپس برای هر بار به‌روزرسانی این بردار یک عضو از مجموعهٔ داده‌های آموزشی را به صورت تصادفی انتخاب کرده و با نرخ ${\displaystyle \alpha }$، بردار حاصل از گرادیان تابع هزینه در نقطه ${\displaystyle \theta }$ را از ${\displaystyle \theta }$ کم می‌کنیم:

${\displaystyle \theta =\theta -\alpha \nabla _{\theta }{\mathcal {J}}_{\boldsymbol {i}}(\theta ;x^{(i)},y^{(i)})}$

که در آن ${\displaystyle {\mathcal {J}}}$تابع هزینه و ${\displaystyle (x^{(i)},y^{(i)})}$یک عضو از داده‌های آموزشی است که به صورت تصادفی انتخاب شده‌است و ${\displaystyle {\mathcal {J}}_{\boldsymbol {i}}(\theta ;x^{(i)},y^{(i)})}$ نشان‌دهندهٔ جملهٔ ${\displaystyle {\boldsymbol {i}}}$ام از جملات تابع هدف است. ${\displaystyle \alpha }$ نرخی است که با آن ${\displaystyle \theta }$ را به‌روزرسانی می‌کنیم و مقداری تجربی دارد که اگر خیلی کوچک باشد زمان رسیدن به همگرایی را طولانی می‌کند و اگر خیلی بزرگ باشد ممکن است همگرایی رخ ندهد.[7]

در پیاده‌سازی دیگر در هر حلقه عضوی تصادفی از مجموعهٔ داده‌ها انتخاب نمی‌شود بلکه در هر حلقه کل مجموعه داده‌ها یک بار به‌صورت تصادفی بازچینی می‌شود سپس به عملیات به‌روزرسانی به ترتیب به ازای ${\displaystyle {\mathcal {J}}_{\boldsymbol {1}},{\mathcal {J}}_{\boldsymbol {1}},...,{\mathcal {J}}_{\boldsymbol {n}}}$ انجام می‌شود که ${\displaystyle {\boldsymbol {n}}}$ نشان‌دهندهٔ اندازهٔ مجموعهٔ داده‌های آموزشی است. شبه کد زیر این پیاده‌سازی را نشان می‌دهد:

به ${\displaystyle \theta }$و ${\displaystyle \alpha }$ مقدار اولیه بده
تا زمانی که کمینه بدست بیاید تکرار کن
داده‌های آموزشی را به صورت تصادفی بازچینی کن
برای  ${\displaystyle {\boldsymbol {i}}}$ از ۱ تا n تکرار کن:
    ${\displaystyle \theta =\theta -\alpha \nabla _{\theta }{\mathcal {J}}_{\boldsymbol {i}}(\theta ;x^{(i)},y^{(i)})}$

همان‌طور که پیشتر اشاره شد معمولاً عملیات به‌روز رسانی برای ${\displaystyle {\mathcal {J}}}$ حاصل از یک تک عضو مجموعهٔ داده‌های آموزشی انجام نمی‌شود و برای زیرمجموعه‌ای از این داده‌ها انجام می‌شود که به آن دستهٔ کوچک می‌گویند.

• 
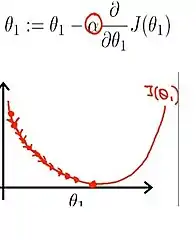  نحوهٔ عملکرد گرادیان کاهشی برای تابع یک ورودی
• 
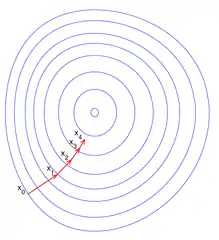  نحوهٔ عملکرد گرادیان کاهشی برای تابع دو ورودی

مثال

فرض کنید در یک مسئلهٔ یادگیری ماشین می‌خواهیم از روش کمترین مربعات استفاده کنیم به طوری که مجموعه‌ای از داده‌های آموزشی به شکل ${\displaystyle (x^{(i)},y^{(i)})}$ داریم که در هر دوتایی، ${\displaystyle x^{(i)}}$ نشان‌دهندهٔ مساحت یک خانه و ${\displaystyle y^{(i)}}$ نشان‌دهندهٔ قیمت خانه به آن مساحت باشد حال اگر بخواهیم نمودار ${\displaystyle y}$ را بر حسب ${\displaystyle x}$ با یک نمدار خطی تقریب بزنیم نیاز به روش کمترین مربعات داریم. طبق این روش بهترین تقریب این نمودار با خط ${\displaystyle ax+b}$ زمانی اتفاق می‌افتد که تابع ${\displaystyle {\mathcal {J}}(a,b)=\left({\frac {1}{2n}}\right)\textstyle \sum _{i=1}^{n}\displaystyle ((ax^{i}+b)-y^{i})}$ کمینه مقدار خود را داشته باشد. حال در این مثال ${\displaystyle {\mathcal {J}}(a,b)}$ تابع هزینه است و به روش گرادیان کاهشی تصادفی می‌شود مقدار ${\displaystyle a,b}$ را بدست آورد که با ازای آن‌ها تابع هزینه کمینه شود و بهترین تقریب خطی یرای نمودار بدست بیاید.[8]

بسط

تا به حال چندین روش نوین برای کاهش سریع‌تر گرادیان کاهشی ابداع شده که ذیلاً بعضی مورد بررسی قرار گرفته‌اند.[9][10][11][12][13]

تکانه (Momentum)

این روش برای اولین بار توسط روملهارت، هیلتون و ویلیامز معرفی شد.[9] در این روش میزان تغییر پارامتر ${\displaystyle \Delta \theta }$ در هر مرحله از بهینه‌سازی ذخیره شده تا در مرحله بعدی به شکل پایین از آن استفاده شود:

${\displaystyle \Delta \theta =\eta \Delta \theta -\alpha \nabla {\mathcal {J}}(\theta )}$

${\displaystyle \theta =\theta +\Delta \theta }$

که با ترکیب این دو به عبارت پایین می‌رسیم:

${\displaystyle \theta =\theta -\alpha \nabla {\mathcal {J_{i}}}(\theta )+\eta \Delta \theta }$

روش momentum باعث می‌شود که مسیر پارامتر ${\displaystyle \theta }$ خیلی تغییر نکند و نوسانات شدیدی نداشته باشد. استفاده از این روش در شبکه‌های عصبی مصنوعی متداول است و معمولاً موجب بهبود دقت شبکه‌های عصبی می‌شود.[14]

میانگین (Averaging)

در این روش در هر مرحله پارامترهای ${\displaystyle t}$ مرحله پیشین ذخیره می‌شود و در نهایت میانگین آنها به عنوان پارامتر بهینه برگردانده می‌شود[10] یعنی ${\displaystyle {\bar {\theta }}={\frac {1}{t}}\sum _{i=0}^{t-1}\theta _{i}}$.

گرادیان تطبیقی (AdaGrad)

روش آداگراد یا گرادیان تطبیقی برای اولین بار در سال ۲۰۱۱ معرفی و منتشر شد.[11][15] این روش برای هر بُعدِ پارامتر یک نرخ یادگیری جداگانه‌ای در نظر می‌گیرد؛ نرخ یادگیری همان ${\displaystyle \alpha }$ در معادله بالاست. برای ابعاد خلوت‌تر (sparse) معمولاً این روش نرخ یادگیری را افزایش می‌دهد و برای ابعادی که مقادیر صفر کمتری دارند نرخ یادگیری را کاهش می‌دهد. این روش اغلب برای مسائلی که با داده‌های خلوت سروکار دارند مانند پردازش تصویر یا زبانهای طبیعی بهینه‌تر است و همگرایی را تسریع می‌بخشد.[11]

نرخ یادگیری برای ابعاد مختلف پارامتر از قطر اصلی ضرب خارجی ${\displaystyle G=\sum _{\tau =1}^{t}g_{\tau }g_{\tau }^{\mathsf {T}}}$ بدست می‌آید. در این معادله ${\displaystyle g_{\tau }=\nabla {\mathcal {J}}_{i}(\theta )}$ گرادیان در مرحله ${\displaystyle \tau }$ است و نرخ یادگیری برای بُعدِ ${\displaystyle j}$ برابر خواهد بود با:

${\displaystyle G_{j,j}=\sum _{\tau =1}^{t}g_{\tau ,j}^{2}}$

حال می‌توان پارامتر را به صورت پایین به‌روز کرد:

${\displaystyle \theta =\theta -\eta \,\mathrm {diag} (G)^{-{\frac {1}{2}}}\circ g}$

این معادله برای بعد ${\displaystyle j}$برابر خواهد بود با:

${\displaystyle \theta _{j}=\theta _{j}-{\frac {\alpha }{\sqrt {G_{j,j}}}}g_{j}.}$

از آنجا که در نرخ یادگیری ${\displaystyle \alpha }$ برای بُعدِ j ام پارامتر بر مقدار ${\displaystyle {\sqrt {G_{i}}}={\sqrt {\sum _{\tau =1}^{t}g_{\tau }^{2}}}}$ تقسیم می‌شود، ابعدای که خلوت‌ترند سریعتر نرخ یادگیری‌شان کاهش می‌یابد.[16] اگرچه روش گرادیان تطبیقی برای مسائل محدب طراحی شده‌است ولی برای مسائل غیر محدب نیز نتایج خوبی به بار آورده‌است.[17]

RMSProp

در این روش همانند گرادیان تطبیقی برای هر بُعدِ پارامتر نرخ یادگیری جداگانه‌ای در نظر گرفته می‌شود.[12] ایده اصلی این است که نرخ یادگیری را برای یک بُعد بر میانگین گرادیان‌های آن بُعد تقسیم کنیم؛ بنابراین، ابتدا میانگین را به این شکل محاسبه می‌کنیم:

${\displaystyle v(\theta ,t)=\gamma v(\theta ,t-1)+(1-\gamma )(\nabla {\mathcal {J}}_{i}(\theta ))^{2}}$

در این معادله ${\displaystyle \gamma }$ ضریب فراموشی است و پارامترها به این صورت بروز می‌شوند:

${\displaystyle \theta =\theta -{\frac {\alpha }{\sqrt {v(\theta ,t)}}}\nabla {\mathcal {J}}_{i}(\theta )}$

این روش نتایج بسیار خوبی برای مسائل مختلف بهینه‌سازی داده‌است.[18]

Adam

این روش مشابه روش RMSProp است با این تفاوت که هم از میانگین گرادیان و هم از گشتاورهای دوم آن به شکل پایین استفاده می‌شود.[13]

${\displaystyle m_{\theta }^{(t+1)}\leftarrow \beta _{1}m_{\theta }^{(t)}+(1-\beta _{1})\nabla _{\theta }J^{(t)}}$

${\displaystyle v_{\theta }^{(t+1)}\leftarrow \beta _{2}v_{\theta }^{(t)}+(1-\beta _{2})(\nabla _{\theta }J^{(t)})^{2}}$

${\displaystyle {\hat {m}}_{\theta }={\frac {m_{\theta }^{(t+1)}}{1-(\beta _{1})^{t+1}}}}$

${\displaystyle {\hat {v}}_{\theta }={\frac {v_{\theta }^{(t+1)}}{1-(\beta _{2})^{t+1}}}}$

${\displaystyle \theta ^{(t+1)}\leftarrow \theta ^{(t)}-\alpha {\frac {{\hat {m}}_{\theta }}{{\sqrt {{\hat {v}}_{\theta }}}+\epsilon }}}$

در اینجا ${\displaystyle \epsilon }$ برای جلوگیری از صفر شدن مخرج است، ${\displaystyle \beta _{1}}$ و ${\displaystyle \beta _{2}}$ ضرایب فراموشی گرادیان و گشتاور دوم گرادیان هستند. مربع گرادیان‌ها مولفه‌ای است. کاربرد ضرایب فراموشی گرادیان و گشتاور دوم گرادیان بیشتر برای جبران فاصله مقدار تقریبی از مقدار واقعی گرادیان می باشد،که معمولا برای زمانی که t کوچک است مفید می باشد. روش Adam رایج ترین روش در شبکه های عصبی عمیق برای تعلیم شبکه می باشد

جستارهای وابسته

رگرسیون خطی

رگرسیون لجیستیک

رگرسیون پواسان

شبکه عصبی مصنوعی

منابع

1. یادکرد خالی (کمک)
2. Mei, Song; Montanari, Andrea; Nguyen, Phan-Minh (2018-08-14). "A mean field view of the landscape of two-layer neural networks". Proceedings of the National Academy of Sciences. 115 (33): E7665–E7671. doi:10.1073/pnas.1806579115. ISSN 0027-8424. PMID 30054315.
3. "Unsupervised Feature Learning and Deep Learning Tutorial". deeplearning.stanford.edu. Archived from the original on 20 اكتبر 2018. Retrieved 2018-10-29. Check date values in: |archivedate= (help)
4. Jenny Rose Finkel, Alex Kleeman, Christopher D. Manning (2008). Efficient, Feature-based, Conditional Random Field Parsing بایگانی‌شده در ۱۴ اوت ۲۰۱۸ توسط Wayback Machine. Proc. Annual Meeting of the ACL.
5. LeCun, Yann A., et al. "Efficient backprop." Neural networks: Tricks of the trade. Springer Berlin Heidelberg, 2012. 9-48
6. Díaz, Esteban and Guitton, Antoine. "Fast full waveform inversion with random shot decimation". SEG Technical Program Expanded Abstracts, 2011. 2804-2808
7. S، Suryansh (۲۰۱۸-۰۳-۱۲). «Gradient Descent: All You Need to Know». Hacker Noon. بایگانی‌شده از اصلی در ۱ مه ۲۰۲۰. دریافت‌شده در ۲۰۱۸-۱۰-۲۹.
8. Miller، Lachlan (۲۰۱۸-۰۱-۱۰). «Machine Learning week 1: Cost Function, Gradient Descent and Univariate Linear Regression». Medium. دریافت‌شده در ۲۰۱۸-۱۰-۲۹.
9. Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (8 October 1986). "Learning representations by back-propagating errors". Nature. 323 (6088): 533–536. Bibcode:1986Natur.323..533R. doi:10.1038/323533a0.
10. Polyak, Boris T.; Juditsky, Anatoli B. (1992). "Acceleration of stochastic approximation by averaging" (PDF). SIAM J. Control Optim. 30 (4): 838–855. doi:10.1137/0330046. Archived from the original (PDF) on 12 January 2016. Retrieved 20 May 2019.
11. Duchi, John; Hazan, Elad; Singer, Yoram (2011). "Adaptive subgradient methods for online learning and stochastic optimization" (PDF). Journal of Machine Learning Research. 12: 2121–2159. Archived from the original (PDF) on 28 May 2019. Retrieved 20 May 2019.
12. Tieleman, Tijmen and Hinton, Geoffrey (2012). Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning
13. Diederik, Kingma; Ba, Jimmy (2014). "Adam: A method for stochastic optimization". arXiv:1412.6980 [cs.LG].
14. Zeiler, Matthew D. (2012). "ADADELTA: An adaptive learning rate method". arXiv:1212.5701 [cs.LG].
15. Perla, Joseph (2014). "Notes on AdaGrad" (PDF). Archived from the original (PDF) on 2015-03-30.
16. Zeiler, Matthew D. (2012). "ADADELTA: An adaptive learning rate method". arXiv:1212.5701 [cs.LG].
17. Gupta, Maya R.; Bengio, Samy; Weston, Jason (2014). "Training highly multiclass classifiers" (PDF). JMLR. 15 (1): 1461–1492. Archived from the original (PDF) on 25 اكتبر 2018. Retrieved 21 مه 2019. Check date values in: |archive-date= (help)
18. Hinton, Geoffrey. "Overview of mini-batch gradient descent" (PDF). pp. 27–29. Archived from the original (PDF) on 23 November 2016. Retrieved 27 September 2016.