چهارتایی آنسکوم
چهارتایی آنسکوم شامل چهار مجموعه دادهاست که دارای آمار توصیفی ساده و تقریباً یکسان هستند، اما توزیعهای بسیار متفاوتی دارند و نمودارهایشان بسیار متفاوت به نظر میرسند. هر مجموعه داده از یازده نقطه ( و ) تشکیل شدهاست. فرانسیس آنسکوم این دادهها را در سال ۱۹۷۳ ساخت تا هم اهمیت رسم نمودار دادهها و هم تأثیر دادههای پرت را بر مدل نهائی نشان داد. وی هدف از انتشار مقاله را مقابله با این تصور که «محاسبات عددی دقیق هستند، اما نمودارها تقریبی هستند» توصیف میکند.[1]
دادهها
برای هر چهار مجموعه، آمارها و ویژگیهای جدول پایین یکسان است:
| آمار | ارزش | دقت |
|---|---|---|
| میانگین | دقیق | |
| واریانس | دقیق | |
| میانگین | ۲ رقم اعشار | |
| واریانس | ۳ ۰٫۰۰۳ | |
| همبستگی و | ۳ رقم اعشار | |
| رگرسیون خطی | به ترتیب به ۲ و ۳ رقم اعشار | |
| ضریب تعیین رگرسیون خطی | ۲ رقم اعشار |
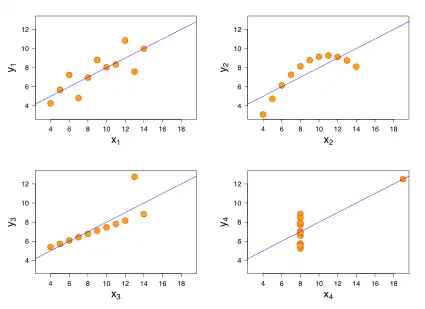
- در اولین نمودار (بالا سمت چپ) به نظر میرسد یک رابطه خطی ساده مربوط به دو متغیر همبسته باشد. در این نمودار از یک توزیع طبیعی پیروی میکند که میانگین آن وابستگی خطی به دارد.
- در نمودار دوم (بالا سمت راست) از یک توزیع طبیعی پیروی نمیکند و رابطه بین دو متغیر خطی نیست. ضریب همبستگی پیرسون اهمیتی ندارد و ضریب تعیین مناسبتر به نظر میرسد بود.
- در نمودار سوم (پایین سمت چپ)، رابطه بین دو متغیر خطی است، اما رگرسیون خطی محاسبه شده به علت وجود یک داده پرت باثبات نیست. داده پرت ضریب را از ۱ به ۰٫۸۱۶ تغییر دادهاست.
- نمودار چهارم (سمت راست پایین) مثالی را نشان میدهد که یک داده پرت برای تولید ضریب همبستگی بالا کفایت میکند، حتی اگر سایر دادهها هیچ ارتباطی بین متغیر مستقل و وابسته نشان ندهند.
این داده چهارتایی هنوز هم اغلب برای نشان دادن اهمیت مصورسازی داده قبل از شروع به تجزیه و تحلیل و عدم کفایت آمارهای توصیفی برای توصیف مجموعه دادهها مورد استفاده قرار میگیرد.[2][3][4][5][6]
مجموعه دادهها به شرح زیر است. مقادیر برای سه مجموعه داده اول یکسان است.[7]
| اول | دوم | سوم | چهارم | ||||
|---|---|---|---|---|---|---|---|
| ۱۰٫۰ | ۸٫۰۴ | ۱۰٫۰ | ۹٫۱۴ | ۱۰٫۰ | ۷٫۴۶ | ۸٫۰ | ۶٫۵۸ |
| ۸٫۰ | ۶٫۹۵ | ۸٫۰ | ۸٫۱۴ | ۸٫۰ | ۶٫۷۷ | ۸٫۰ | ۵٫۷۶ |
| ۱۳٫۰ | ۷٫۵۸ | ۱۳٫۰ | ۸٫۷۴ | ۱۳٫۰ | ۱۲٫۷۴ | ۸٫۰ | ۷٫۷۱ |
| ۹٫۰ | ۸٫۸۱ | ۹٫۰ | ۸٫۷۷ | ۹٫۰ | ۷٫۱۱ | ۸٫۰ | ۸٫۸۴ |
| ۱۱٫۰ | ۸٫۳۳ | ۱۱٫۰ | ۹٫۲۶ | ۱۱٫۰ | ۷٫۸۱ | ۸٫۰ | ۸٫۴۷ |
| ۱۴٫۰ | ۹٫۹۶ | ۱۴٫۰ | ۸٫۱۰ | ۱۴٫۰ | ۸٫۸۴ | ۸٫۰ | ۷٫۰۴ |
| ۶٫۰ | ۷٫۲۴ | ۶٫۰ | ۶٫۱۳ | ۶٫۰ | ۶٫۰۸ | ۸٫۰ | ۵٫۲۵ |
| ۴٫۰ | ۴٫۲۶ | ۴٫۰ | ۳٫۱۰ | ۴٫۰ | ۵٫۳۹ | ۱۹٫۰ | ۱۲٫۵۰ |
| ۱۲٫۰ | ۱۰٫۸۴ | ۱۲٫۰ | ۹٫۱۳ | ۱۲٫۰ | ۸٫۱۵ | ۸٫۰ | ۵٫۵۶ |
| ۷٫۰ | ۴٫۸۲ | ۷٫۰ | ۷٫۲۶ | ۷٫۰ | ۶٫۴۲ | ۸٫۰ | ۷٫۹۱ |
| ۵٫۰ | ۵٫۶۸ | ۵٫۰ | ۴٫۷۴ | ۵٫۰ | ۵٫۷۳ | ۸٫۰ | ۶٫۸۹ |
مشخص نیست که چگونه آنسکوم مجموعه دادههای خود را ایجاد کرد.[8] از زمان انتشار آن، روشهای مختلفی برای تولید مجموعه دادههای مشابه با آمارهای یکسان و نمودارهای متفاوت ایجاد شدهاست.[9]
منابع
- Anscombe, F. J. (1973). "Graphs in Statistical Analysis". American Statistician. 27 (1): 17–21. doi:10.1080/00031305.1973.10478966. JSTOR 2682899.
- Elert, Glenn. "Linear Regression". The Physics Hypertextbook.
- Janert, Philipp K. (2010). 978-0-596-80235-6/page/65 Data Analysis with Open Source Tools Check
|url=value (help). O'Reilly Media. pp. 978-0-596-80235-6/page/65 65–66. ISBN 0-596-80235-8. - Chatterjee, Samprit; Hadi, Ali S. (2006). Regression Analysis by Example. John Wiley and Sons. p. 91. ISBN 0-471-74696-7.
- Saville, David J.; Wood, Graham R. (1991). Statistical Methods: The geometric approach. Springer Science+Business Media|Springer. p. 418. ISBN 0-387-97517-9.
- Tufte, Edward R. (2001). The Visual Display of Quantitative Information (2nd ed.). Cheshire, CT: Graphics Press. ISBN 0-9613921-4-2.
- Anscombe, F. J. (1973). "Graphs in Statistical Analysis". American Statistician. 27 (1): 17–21. doi:10.1080/00031305.1973.10478966. JSTOR 2682899.
- Chatterjee, Sangit; Firat, Aykut (2007). "Generating Data with Identical Statistics but Dissimilar Graphics: A follow up to the Anscombe dataset". The American Statistician. 61 (3): 248–254. doi:10.1198/000313007X220057. JSTOR 27643902.
- Matejka, Justin; Fitzmaurice, George (2017). "Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing". Conference on Human Factors in Computing Systems|Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems: 1290–1294. doi:10.1145/3025453.3025912.