انتگرال

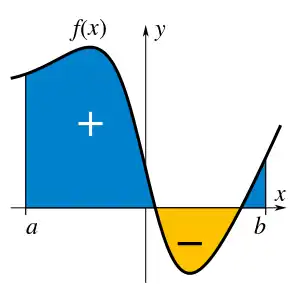
در ریاضیات، انتگرال (به فرانسوی: Integral)، روشی برای اختصاص اعداد به توابع است، به گونه‌ای که جابجایی، مساحت، حجم و دیگر مفاهیم برآمده از ترکیب داده‌های بی‌نهایت کوچک را به وسیله آن بتوان توصیف کرد. انتگرال‌گیری یکی از دو عمل مهم در حساب دیفرانسیل و انتگرال است، که عمل دیگر آن (عمل معکوس) دیفرانسیل‌گیری یا همان مشتق‌گیری است. برای تابع داده شده‌ای چون f از متغیر حقیقی x و بازه ${\displaystyle [a,b]}$ از خط حقیقی، انتگرال معین:

${\displaystyle \int _{a}^{b}f(x)\,dx}$

انتگرال معین تابعی را می‌توان به صورت مساحت علامت دار ناحیه ای محدود به نمودار آن تابع نشان داد.

بخشی از سری مقالات
حسابان
قضیه اساسی قاعده انتگرال گیری لایبنیز حد توابع پیوستگی قضیه مقدار میانگین قضیه رول
دیفرانسیل تعاریف مشتق (تعمیم‌ها) دیفرانسیل بی‌نهایت‌کوچک‌ها از یک تابع کلی مفاهیم نمادگذاری دیفرانسیل گیری مشتق دوم دیفرانسیل گیری ضمنی دیفرانسیل گیری لگاریتمی نرخ های مرتبط قضیه تیلور قواعد و اتحادها جمع ضرب زنجیره توان خارج قسمت قاعده هوپیتال معکوس لایبنیز عمومی فرمول فا دی برونو
انتگرال لیست انتگرال‌ها تبدیل انتگرالی تعاریف پادمشتق انتگرال (نامعین) انتگرال ریمانی انتگرال لبگ انتگرال کانتور انتگرال توابع معکوس انتگرال گیری توسط جزء به جزء دیسک ها پوسته‌های سیلندری تغییر متغیر (مثلثاتی, وایرشتراس, اویلر) فرمول اویلر کسرهای جزئی تغییر ترتیب فرمول کاهش دیفرانسیل گیری زیر نماد انتگرال
سری هندسی (حسابی-هندسی) هارمونیک متناوب توانی دوجمله‌ای تیلور آزمون‌های همگرایی حد جمعوند (آزمون جمله) نسبت ریشه انتگرال آزمون مقایسه مقایسه حدی سری‌های متناوب چگالی کوشی دیریکله آبل
بردار گرادیان دیورژانس کرل لاپلاس مشتق جهتی اتحادها قضایا گرادیان گرین استوکس دیورژانس استوکس تعمیم یافته
چندمتغیره فرمالیسم‌ها ماتریس تنسور خارجی هندسی تعاریف مشتق جزئی انتگرال چندگانه انتگرال خطی انتگرال سطحی انتگرال حجمی ژاکوبی هسین
تخصصی کسری مالیاوین تصادفی تغییرات
متفرقه پیش-حسابان تاریخچه واژه‌نامه فهرست موضوعا

به‌طور صوری به عنوان مساحت علامت‌دار ناحیه ای از صفحه xy که به نمودار f، محور x و خطوط عمودی x=a و x=b محدود شده‌است. نواحی بالای محور x به مساحت کل افزوده و نواحی پایین محور x از ان می‌کاهند.

عملیات انتگرال‌گیری، در حد یک مقدار ثابت (یعنی بدون در نظر گرفتن یک مقدار ثابت)، معکوس عملیات دیفرانسیل‌گیری است. بدین منظور، اصطلاح انتگرال را می‌توان به معنای پاد-مشتق نیز به کار برد، یعنی تابعی چون F که مشتقش تابع داده شده‌ی f باشد. در این حالت به انتگرال f، انتگرال نامعین گفته شده و به صورت زیر نوشته می‌شود:

${\displaystyle F(x)=\int f(x)\,dx.}$

انتگرال‌هایی که در این مقاله مورد بحث قرار می‌گیرند از نوع انتگرال معین اند. قضیه اساسی حساب، دیفرانسیل‌گیری را به انتگرال معین ارتباط می‌دهد: اگر f یک تابع پیوسته حقیقی مقدار روی بازهٔ ${\displaystyle [a,b]}$ باشد، آنگاه زمانی که پاد مشتق f یعنی F، معلوم باشد، انتگرال f روی آن بازه مساوی است با:

${\displaystyle \int _{a}^{b}\,f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a)\,.}$

اصول انتگرال‌گیری به‌طور مستقل توسط اسحاق نیوتون و گوتفرید ویلهلم لایبنیز در اواخر قرن هفدهم میلادی قاعده‌بندی شد، آن‌ها انتگرال را به صورت جمع مستطیل‌هایی با عرض‌های بی‌نهایت کوچک می‌دیدند. برنارد ریمان تعریف دقیقی از انتگرال ارائه نمود. این تعریف بر اساس فرایند حد گیری است که مساحت زیر نمودار یک خم را با شکستن آن ناحیه به قطعات نازک عمودی تخمین می‌زند. با شروع قرن نوزدهم میلادی، مفاهیم پیچیده‌تری از انتگرال ظهور پیدا کرد که در آن نوع تابع به علاوه دامنه انتگرال‌گیری تعمیم یافت. انتگرال خطی برای توابع دو یا چند متغیره تعریف شده‌است و بازه انتگرال‌گیری ${\displaystyle [a,b]}$ در آن با خمی که دو نقطه ابتدا و انتهای انتگرال‌گیری را به هم متصل می‌کند جایگزین شده‌است. در انتگرال سطح (یا انتگرال رویه ای)، خم با یک رویه در فضای سه بعدی جایگزین می‌شود.

تاریخچه

قبل از حسابان

اولین تکنیک نظام مندی که قادر به تعیین انتگرال، روش افنا بود که توسط ستاره‌شناس یونان باستان، اودوکسوس (حدود ۳۷۰ قبل از میلاد) معرفی شد. در این روش مساحت‌ها و حجم‌ها به تعداد نامتناهی تکه که مساحت یا حجم هر کدام از آن تکه‌ها معلوم بود تقسیم‌بندی می‌شدند. ارشمیدس این روش را ارتقاء داده و از آن در قرن سوم قبل از میلاد استفاده کرد تا مساحت‌های سهمی و دایره را به کمک آن بدست آورد.

روش مشابهی به‌طور مستقل در حدود قرن سوم بعد از میلاد توسط میو هوی در چین بدست آمد، او از این روش برای بدست آوردن مساحت دایره استفاده کرد. این روش بعدها در قرن پنجم میلادی توسط ریاضیدانان پدر و پسر چینی یعنی زو چونگژی و زو گنگ برای بدست آوردن حجم یک کره (Shea 2007; Katz 2004، صص. ۱۲۵–۱۲۶) مورد استفاده قرار گرفت.

در خاورمیانه، حسن ابن الهیثم (نام لاتین شده او Alhazen است) (۹۶۵–۱۰۴۰ میلادی) فرمولی برای جمع توان‌های چهارم بدست آورد. او از این فرمول برای بدست آوردن چیزی استفاده کرد که اکنون می‌دانیم انتگرال آن تابع است، وی از آن برای محاسبه حجم یک سهمی گون استفاده نمود.[1]

تا قرن هفدهم میلادی پیشرفت مهمی در حساب انتگرال صورت نگرفت. در این زمان بود که روش کاوالیری یعنی روش تقسیم ناپذیرها، و همچنین کارهای فرما، بنیانگذاری حساب مدرن را کلید زدند. کاوالیری در فرمول‌های مربع کاوالیری خود، انتگرالهای ${\displaystyle x^{n}}$ را تا درجه n=۹ محاسبه کرد. قدم‌های بعدی در اوایل قرن هفدهم میلادی توسط بارو و توریسلی برداشته شد، آن‌ها اولین نشانه‌های ارتباط انتگرال و دیفرانسیل را ارائه نمودند. بارو اولین اثبات قضیه اساسی حساب را ارائه داد. والیس روش کاوالیری را برای محاسبه انتگرال‌های توان‌های عمومی x تعمیم داد، به گونه ای که شامل توان‌های منفی و حتی توان‌های کسری نیز می‌شد.

نیوتون و لایبنیز

در قرن هفدهم میلادی، با اکتشافات مستقل قضیه اساسی حساب توسط لایبنیز و نیوتون، پیشرفت عمده ای در انتگرال‌گیری به‌وجود آمد. لایبنیز کار خود در ارتباط با حساب را قبل از نیوتون منتشر کرد. این قضیه ارتباطی بین انتگرال‌گیری و دیفرانسیل‌گیری را اثبات می‌کند. این ارتباط، از ترکیب سادگی نسبی دیفرانسیل‌گیری استفاده کرده و از آن در جهت فرایند انتگرال‌گیری استفاده می‌کند. به‌خصوص، قضیه بنیادی حساب امکان حل دسته وسیع تری از مسائل را می‌دهد. چارچوب ریاضیاتی جامعی که هردوی لایبنیز و نیوتون به‌وجود آوردند از نظر اهمیت در یک سطح هستند. با استفاده از مفهوم حساب بی‌نهایت کوچک‌ها، امکان تحلیل دقیق توابع با دامنه‌های پیوسته فراهم گشت. این چارچوب در نهایت منجر به ایجاد حسابان شد، ضمن این که نماد انتگرال‌گیری در حسابان به‌طور مستقیم از کارهای لایبنیز برگرفته شده‌است.

صوری سازی

درحالی که نیوتون و لایبنیز رهیافت نظام مندی به انتگرال‌گیری ارائه نمودند، کارهای آن‌ها فاقد درجه ای از استواری و استحکام ریاضیاتی بود. بیشاپ برکلی، حمله بیاد ماندنی به روش افزایش ناپدید شونده نیوتون کرد و آن را «ارواح کمیت‌های مرده» نامید. با توسعه حد، حسابان مجهز به بنیان مستحکمی گشت. ابتدا انتگرال‌گیری با کمک حدود توسط ریمان از نظر ریاضیاتی مستحکم شد. گرچه که تمام توابع تکه به تکه پیوسته در بازه ای کراندار ریمان-انتگرال پذیرند، اما مثلاً به‌طور خاص در بستر آنالیز فوریه با توابعی سروکار داریم که بر اساس روش ریمانی انتگرال پذیر نیستند، لذا به مرور با توسعه تعریف انتگرال‌گیری، مثل فرمول انتگرال‌گیری لبگ، توابع بیشتری در دایره توابع انتگرال پذیر قرار گرفتند و بدین طریق نظریه اندازه (زیر شاخه ای از آنالیز حقیقی) شکل گرفت. تعاریف دیگر انتگرال که هردو رهیافت ریمانی و لبگ را بسط می‌دهند نیز پیشنهاد شده‌اند. این رهیافت‌ها بر اساس سیستم اعداد حقیقی بوده و امروزه رایج اند، اما رهیافت‌های دیگری نیز وجود دارند که بر اساس دستگاه اعداد فراحقیقی بنیان نهاده شده‌اند و از بخش استاندارد (مربوط به آنالیز غیر استاندارد) جمع بی‌نهایت ریمانی برای تعریف انتگرال استفاده می‌کنند.

مهم‌ترین تعاریف در انتگرال

مثالی از انتگرال با تقسیمات ناهمسان (بزرگترین قسمت با رنگ قرمز مشخص شده‌است)

همگرایی مجموع‌های ریمان

از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لِبِگ است. انتگرال ریمان به‌وسیله برنهارد ریمان در سال ۱۸۵۴ ارائه شد که تعریف دقیقی را از انتگرال ارائه می‌داد تعریف دیگر را هانری لبگ ارائه داد که طبق این تعریف شرایط تعویض‌پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می‌کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال می‌توان به انتگرال ریمان–استیلتیس اشاره کرد. پس به‌طور خلاصه سه تعریف زیر از مهم‌ترین تعاریف انتگرال می‌باشند:

محاسبه انتگرال

تخمین انتگرال ${\displaystyle {\sqrt {x}}}$ از ۰ تا 1

اکثر روش‌های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده‌است که بر طبق آن داریم:

1. f تابعی در بازه (a,b) در نظر می‌گیریم.
2. پاد مشتق f را پیدا می‌کنیم که تابعی است مانند f.
3. قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می‌گیریم؛ بنابراین مقدار انتگرال ما برابر خواهد بود.

به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می‌دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار ساده‌ای نیست و نیاز به استفاده از تکنیک‌های انتگرال‌گیری دارد این تکنیک‌ها عبارت‌اند از:

• انتگرال‌گیری به‌وسیله تغییر متغیر
• انتگرال‌گیری جزء به جزء: ${\displaystyle \int u\,dv=uv-\int v\,du}$
• انتگرال‌گیری با تغییر متغیر مثلثاتی
• انتگرال‌گیری به‌وسیله تجزیه کسرها

روش‌هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می‌رود همچنین می‌توان بعضی از انتگرال‌ها با ترفندهایی حل کرد برای مثال می‌توانید به انتگرال گاوسی مراجعه کنید.

تقریب انتگرال‌های معین

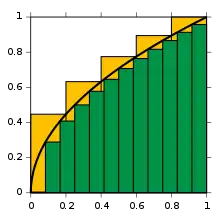
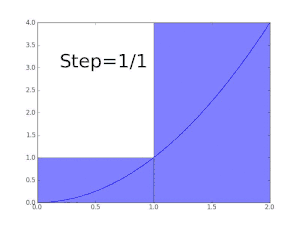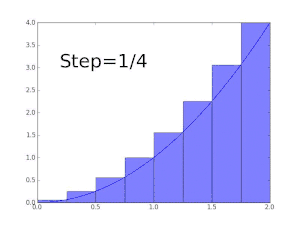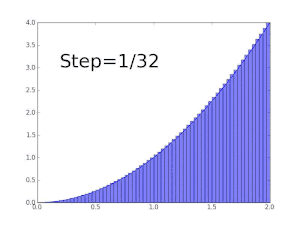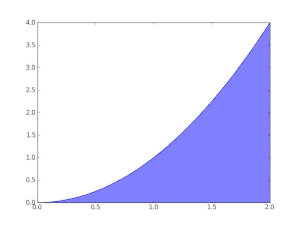
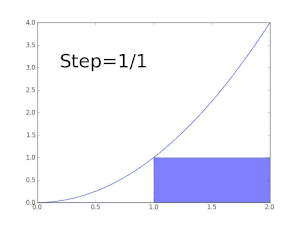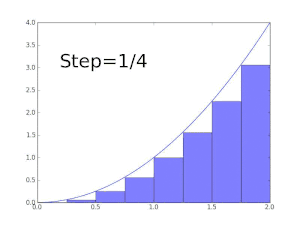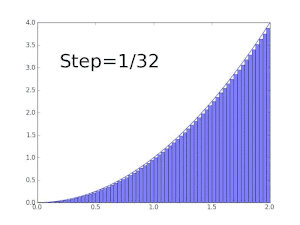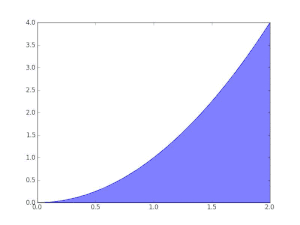
محاسبه سطح زیر نمودار به‌وسیله مستطیل‌هایی زیر نمودار. هر چه قدر عرض مستطیل‌ها کوچک می‌شوند مقدار دقیق تری از مقدار انتگرال بدست می‌آید.

انتگرال‌های معین ممکن است با استفاده از روش‌های انتگرال‌گیری عددی، تخمین زده شوند. یکی از عمومی‌ترین روش‌ها، روش مستطیلی نامیده می‌شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آن‌ها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش‌هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه‌ای است. اگر چه روش‌های عددی مقدار دقیق انتگرال را به ما نمی‌دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می‌کند.

جمع داربو

جمع بالایی داربو برای تابع ${\displaystyle y=x^{2}}$

جمع پایینی داربو برای تابع ${\displaystyle y=x^{2}}$

کاربرد

انتگرال‌ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک می‌توان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست می‌آید. اما به‌طور کلی می‌توان آن را تغییرات کمیت حاصل ضرب افقی و عمودی نمودار نامید مثلاً: در یک رابطه کمیت‌ها را تحلیل ابعادی می‌کنیم مثلاً رابطه سرعت و زمان را به صورت زیر نوشته می‌شود:

${\displaystyle v=[L]/[T]t=[T]\!}$

سپس دو تحلیل را در هم ضرب می‌کنیم:

${\displaystyle [L]\!}$

پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.

پانویس

1. Katz, V.J. 1995. "Ideas of Calculus in Islam and India." Mathematics Magazine (Mathematical Association of America), 68(3):163–174.

• مشارکت‌کنندگان ویکی‌پدیا. «Cantor's Theorem». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۳ نوامبر ۲۰۱۹.

کتابشناسی

• Apostol, Tom M. (1967), Calculus, Vol.  1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1
• Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1. In particular chapters III and IV.
• Burton, David M. (2005), The History of Mathematics: An Introduction (6th ed.), McGraw-Hill, p. 359, ISBN 978-0-07-305189-5
• Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, pp. 247–252, ISBN 978-0-486-67766-8
• Dahlquist, Germund; Björck, Åke (2008), "Chapter 5: Numerical Integration", Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, archived from the original on 2007-06-15
• Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231
  Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, pp. 200–201
• Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4
  (Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H. (1953), "Integration in abstract spaces", Bulletin of the American Mathematical Society, 59 (2): 111–139, doi:10.1090/S0002-9904-1953-09694-X, ISSN 0273-0979
• Kahaner, David; Moler, Cleve; Nash, Stephen (1989), "Chapter 5: Numerical Quadrature", Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8
• Kallio, Bruce Victor (1966), A History of the Definite Integral (PDF) (M.A. thesis), University of British Columbia, archived from the original (PDF) on 5 March 2014, retrieved 5 December 2019
• Katz, Victor J. (2004), A History of Mathematics, Brief Version, Addison-Wesley, ISBN 978-0-321-16193-2
• Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel, ed., Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller
• Lieb, Elliott; Loss, Michael (2001), Analysis, Graduate Studies in Mathematics, 14 (2nd ed.), American Mathematical Society, ISBN 978-0-8218-2783-3
• Miller, Jeff, Earliest Uses of Symbols of Calculus, retrieved 2009-11-22
• O’Connor, J. J.; Robertson, E. F. (1996), A history of the calculus, retrieved 2007-07-09
• Rudin, Walter (1987), "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
• Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover
• Shea, Marilyn (May 2007), Biography of Zu Chongzhi, University of Maine, archived from the original on 14 June 2010, retrieved 9 January 2009
• Siegmund-Schultze, Reinhard (2008), "Henri Lebesgue", in Timothy Gowers; June Barrow-Green; Imre Leader, Princeton Companion to Mathematics, Princeton University Press.
• Stoer, Josef; Bulirsch, Roland (2002), "Topics in Integration", Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3.
• W3C (2006), Arabic mathematical notation

پیوند به بیرون

• "Integral", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Online Integral Calculator, Wolfram Alpha.
• Online Integral Calculator, by MathsTools.

• انتگرال چیست و به چه درد می‌خورد؟
• علت حذف انتگرال از کتب دانش‌آموزان ایران

کتاب‌های برخط

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K. D. , A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Johnson, William Woolsey (1909) Elementary Treatise on Integral Calculus, link from HathiTrust.
• Kowalk, W. P. , Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute
• P. S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) — a cookbook of definite integral techniques