انتگرال سطحی
انتگرال سطحی (Surface integral ) در ریاضیات، یک انتگرال معین است که بر روی یک سطح گرفته میشود. این انتگرال، میتواند بهعنوان نظیر دوگانه انتگرال خطی در نظر گرفته شود. با داشتن یک سطح، انتگرالگیری میتواند بر روی میدانهای نردهای (توابعی که مقدار آنها یک کمیت نردهای است) یا برداری آن (توابعی که مقدار آنها یک بردار اقلیدسی است) انجام گیرد.
| بخشی از سری مقالات |
| حسابان |
|---|
|
انتگرالگیری بر روی سطوح، در فیزیک و بهویژه در نظریهٔ کلاسیک الکترومغناطیس کاربرد دارد.
انتگرال سطحی میدانهای نردهای


برای یافتن یک فرمول صریح برای انتگرال سطحی، باید سطح مورد نظر، S، بر حسب یک دستگاه مختصات خمیده بر روی آن بیان شود (مانند دستگاه مختصات جغرافیایی روی یک کره). اگر چنین بیانی بهصورت فرض شود که در یک ناحیه T بر روی صفحه تغییر میکنند، آنگاه انتگرال روی سطح بهصورت زیر نوشته میشود:
که عبارت داخل خطوط عمودی در سمت راست معادلهٔ بالا، اندازه بردار حاصلضرب خارجی مشتقهای پارهای بوده و المان سطح نامیده میشود.
برای مثال، برای محاسبهٔ مساحت رویهٔ یک تابع نردهای مانند ، میتوان روابط زیر را نوشت:
که . بنابراین، و . در نتیجه با جایگذاری این مقادیر:
با توجه به استفاده از ضرب خارجی، فرمولهای بالا فقط برای سطوح واقع در فضای سهبعدی معتبرند.
انتگرال سطحی میدانهای برداری
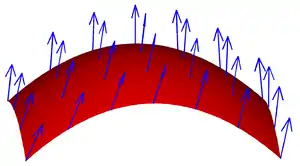
اگر یک میدان برداری بر روی باشد، یعنی بهازای هر در ، یک بردار باشد، انتگرال سطحی این میدان برداری، برداری خواهد بود که هر مؤلفهٔ آن، انتگرال سطحی مؤلفهٔ متناظر آن میدان بر طبق تعریف انتگرال سطحی میدانهای نردهای است.
انتگرال مؤلفهٔ عمودی هر میدان برداری، یک کمیت نردهای است. اگر یک سیال از سطح بگذرد بهگونهای که سرعت سیال را در نشان دهد، شار گذرنده از سطح برابر با انتگرال سطحی بر روی است. اگر میدان برداری، مماس بر باشد، شار گذرنده صفر است، زیرا سیال فقط موازی سطح در جریان بوده و به داخل یا بیرون آن نمیرود. ولی اگر تنها در راستای سطح نبوده و علاوه بر مؤلفهٔ مماسی، مؤلفهٔ عمودی هم داشته باشد، سپس تنها مؤلفهٔ عمودی باعث ایجاد شار خواهد شد. بنابراین برای یافتن شار گذرنده از سطح، باید اندازه تصویر بردار بر روی بردار عمود بر سطح یا به عبارت دیگر، ضرب داخلی در بردار عمود بر سطح در هر نقطه (که حاصل آن یک میدان نردهای خواهد بود)، محاسبه شده و انتگرالگیری شود:
قضیههای مرتبط با انتگرال سطحی
با استفاده از هندسه دیفرانسیل و حساب برداری، نتایج مفید متنوعی برای انتگرالهای سطحی بدست میآیند، از جمله قضیه دیورژانس و قضیه استوکس.