جانشینی مثلثاتی
جانشینی مثلثاتی(به انگلیسی: Trigonometric substitution) در ریاضیات و در محاسبه انتگرال توابع به منظور سادهتر کردن توابع به کار میرود.مثلاً برای تبدیل عبارات رادیکالی و نمایی میتوان از این تبدیلها استفاده کرد[1][2].
- اگر انتگرال شامل عبارت a2 − x2 باشد:
| بخشی از سری مقالات |
| حسابان |
|---|
|
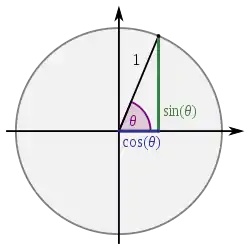
| مثلثات |
|---|
 |
| منابع |
| قوانین و قضایا |
| حساب دیفرانسیل و انتگرال |
و از اتحاد مثلثاتی زیر استفاده می کنیم:
- اگر انتگرال شامل عبارت a2 + x2, باشد:
- از اتحاد مثلثاتی زیر استفاده می کنیم:
- گر انتگرال شامل عبارت x2 − a2, باشد:
- از اتحاد مثلثاتی زیر استفاده می کنیم:
چند نمونه
انتگرالهای شامل g a2 − x2 در انتگرال زیر:
می توان از روابط مثلثاتی زیر استفاده کرد:
باید توجه داشت که در نمونه فوق باید همواره a> 0
نکته دیگر تغییر حدود انتگرال برای انتگرالهای معین است.مثلاً اگر x از 0 تا a/2 تغییر کند،sin(θ) از 0 تا 1/2 تغییر میکند ،در نتیجه θ از 0 تا π/6 تغییر میکند:
منابع
- Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 0-495-01166-5.
- Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 0-321-58876-2.
| Wikiversity has learning materials about Trigonometric Substitutions |
| در ویکیکتاب کتابی با عنوان: Calculus/Integration techniques/Trigonometric Substitution وجود دارد. |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.