قانون کتانژانت‌ها

در مثلثات، قانون کتانژانت‌ها به رابطه میان اندازه ضلع‌های یک مثلث و کتانژانت نصف سه زاویه آن گفته می‌شود. سه مقداری که برابریشان در قانون کتانژانت‌ها ثابت می‌شود، برابر با شعاع دایره محاطی مثلث مورد نظر هستند.

یک مثلث به همراه دایره محاطی آن که هر ضلع را به دو بخش، تقسیم می‌کند. نیمسازها در مرکز دایره، همرس هستند.

شش بخش ضلع‌های تقسیم شده

تعریف

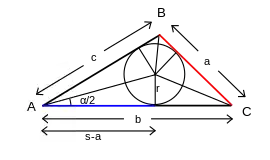
با استفاده از نام‌گذاری متداول برای مثلث (مانند شکل روبرو) که a و b و c ضلع‌ها، A و B و C رأس‌ها و α و β و γ زاویه‌های مثلث، s نصف محیط مثلث (که مقدار آن برابر s = (a+b+c)/2 است) و r شعاع دایره محاطی هستند، قانون کتانژانت‌ها به صورت زیر بیان می‌شود:

{\frac {\cot(\alpha /2)}{s-a}}={\frac {\cot(\beta /2)}{s-b}}={\frac {\cot(\gamma /2)}{s-c}}={\frac {1}{r}}

و شعاع دایره محاطی از رابطه زیر به دست می‌آید:

r={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}}

اثبات

نقطه تماس دایره محاطی با هر ضلع، آن را به دو بخش تقسیم می‌کند. هر دو بخش مجاور یک رأس با یکدیگر برابر هستند. اگر از هر جفت مجاور یک رأس، یکی انتخاب شود، مجموع این سه برابر s نصف محیط مثلث است. برای نمونه، جمع دو خط آبی و قرمز در شکل روبرو برابر s می‌باشد. اکنون با استفاده از تعریف تابع کتانژانت، داریم:

\cot(\alpha /2)={\frac {s-a}{r}}\,

رابطه مشابهی برای دو زاویه دیگر به دست می‌آید. به این ترتیب، بخش اول قانون کتانژانت‌ها ثابت می‌شود.

برای بخش دوم، از اتحاد جمع دو زاویه بهره می‌بریم:

\cot(u+v+w)={\frac {\cot u+\cot v+\cot w-\cot u\cot v\cot w}{1-\cot u\cot v-\cot v\cot w-\cot w\cot u}}

از آن‌جایی که $\cot(\alpha /2+\beta /2+\gamma /2)=\cot(\pi /2)=0$ ، رابطه بالا به صورت زیر در می‌آید:

\cot(\alpha /2)\cot(\beta /2)\cot(\gamma /2)=\cot(\alpha /2)+\cot(\beta /2)+\cot(\gamma /2)

با جایگذاری مقادیر به دست آمده از بخش اول، نتیجه می‌شود:

{\frac {s-a}{r}}{\frac {s-b}{r}}{\frac {s-c}{r}}={\frac {s-a}{r}}+{\frac {s-b}{r}}+{\frac {s-c}{r}}

طرف راست رابطه بالا برابر s/r است. به این ترتیب، بخش دوم قانون کتانژانت‌ها ثابت می‌شود.

چند اثبات با استفاده از قانون کتانژانت‌ها

چند رابطه دیگر، از قانون کتانژانت‌ها به دست می‌آیند:

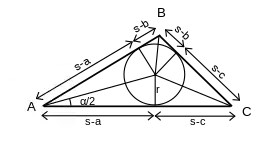
فرمول هرون. مثلث ABC به ۶ مثلث قائم‌الزاویه کوچکتر، تقسیم می‌شود. هر دو مثلث مجاور یک رأس، دارای قاعده و ارتفاع برابر با یکدیگر هستند. مثلاً دو مثلث مجاور رأس A دارای قاعده s-a و ارتفاع r هستند. بنابراین مساحت آن مثلث، ${\tfrac {1}{2}}r(s-a)$ و مساحت دو مثلث مجاور (r(s-a است. به این ترتیب، مساحت مثلث ABC از رابطه زیر محاسبه می‌شود:

{\begin{aligned}S&=r(s-a)+r(s-b)+r(s-c)=r(s-a+s-b+s-c)\\[8pt]&=r(3s-(a+b+c))=r(3s-2s)=rs\\[8pt]\end{aligned}}

که فرمول هرون را نتیجه می‌دهد:

S={\sqrt {s(s-a)(s-b)(s-c)}}

فرمول اول مولواید: از اتحاد جمع دو زاویه و قانون کتانژانت‌ها داریم:

{\frac {\sin(\alpha /2-\beta /2)}{\sin(\alpha /2+\beta /2)}}={\frac {\cot(\beta /2)-\cot(\alpha /2)}{\cot(\beta /2)+\cot(\alpha /2)}}={\frac {a-b}{2s-a-b}}

که نتیجه می‌دهد:

{\dfrac {a-b}{c}}={\dfrac {\sin(\alpha /2-\beta /2)}{\cos(\gamma /2)}}

فرمول دوم مولواید: از اتحاد جمع دو زاویه و قانون کتانژانت‌ها داریم:

{\frac {\cos(\alpha /2-\beta /2)}{\cos(\alpha /2+\beta /2)}}={\frac {\cot(\alpha /2)\cot(\beta /2)+1}{\cot(\alpha /2)\cot(\beta /2)-1}}

={\frac {\cot(\alpha /2)+\cot \left(\beta /2\right)+2\cot(\gamma /2)}{\cot(\alpha /2)+\cot(\beta /2)}}={\frac {4s-a-b-2c}{2s-a-b}}

اکنون، پس از تبدیل ضرب به جمع، رابطه زیر به دست می‌آید:

{\dfrac {b+a}{c}}={\dfrac {\cos(\alpha /2-\beta /2)}{\sin(\gamma /2)}}

جستارهای وابسته

پیوند به بیرون

«Formula sheet database – law of cotangents». دریافت‌شده در ۱۷ فروردین ۱۳۹۴.

منابع

Silvester، John R. (۲۰۰۱). Geometry: Ancient and Modern. Oxford University Press. ص. ۳۱۳. شابک ۹۷۸۰۱۹۸۵۰۸۲۵۰.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.