تابع چگالی احتمال

در آمار و احتمال، به بیان ساده، تابعِ چگالیِ احتمالِ یک متغیر تصادفی پیوسته به تابعی گفته می‌شود که انتگرال آن در هر بازهٔ معین، برابر با احتمال قرار داشتن متغیر تصادفی در آن بازه است.[1]

بنابراین، احتمال این‌که یک متغیر تصادفی پیوسته، یک مقدار معیّن اختیار کند، صفر است.

مقدار تابع چگالی احتمال همواره غیرمنفی است.

توزیع پیوسته یک‌متغیره

تابع توزیع نرمال N(0, σ²).

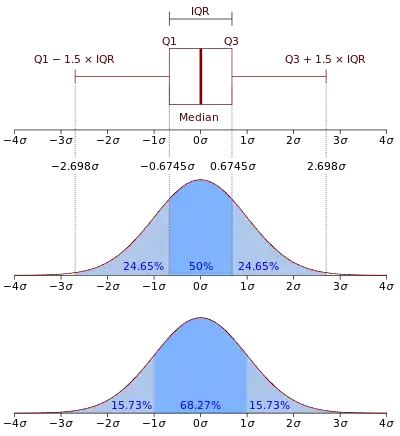
احتمال آنکه متغیر تصادفی X در بازه [a,b] واقع شود از رابطهٔ زیر بدست می‌آید:[2]

${\displaystyle \Pr(a\leq X\leq b)=\int _{a}^{b}f(x)\,dx}$

همچنین کل مساحت زیر نمودار برابر است با ۱؛ یعنی:

${\displaystyle \int _{-\infty }^{\infty }\,f(x)\,dx=1}$

در نتیجه تابع توزیع تجمعی را می‌توان به صورت زیر نوشت:

${\displaystyle F(x)=\int _{-\infty }^{x}f(u)\,\mathrm {d} u,}$

و اگر f تابعی پیوسته باشد:

${\displaystyle f(x)={\frac {\mathrm {d} }{\mathrm {d} x}}F(x).}$

تعریف

متغیر تصادفی X را در نظر بگیرید که مقدار آن در فضای اندازه ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ تعریف شده و توزیع احتمال آن اندازه X_∗P در ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ است، آنگاه چگالی X نسبت به اندازه مرجع μ در ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ بواسطه مشتق رادون−نیکودیم به شکل زیر تعریف می‌شود:

${\displaystyle f={\frac {\mathrm {d} X_{*}P}{\mathrm {d} \mu }}.}$

به عبارت دیگر، به ازای هر مجموعه اندازه‌پذیر ${\displaystyle A\in {\mathcal {A}}}$، f می‌تواند هر تابع قابل اندازه‌گیری با ویژگی زیر باشد:

${\displaystyle \Pr[X\in A]=\int _{X^{-1}A}\,\mathrm {d} P=\int _{A}f\,\mathrm {d} \mu }$

برخلاف احتمالی که به یک متغیر تصادفی گسسته نسبت داده می‌شود، تابع چگالی احتمال می‌تواند مقادیر بیشتر از یک را نیز اختیار کند. به‌طور مثال توزیع یکنواخت در بازه [۱/۲ ،۰] چگالی احتمالی f(x) = ۲ برای ۰ ≤ x ≤ ½ دارد و f(x) = ۰ برای خارج این بازه دارد با داشتن تابع چگالی احتمالی متغیر تصادفی X می‌توان مقدار امید ریاضی آن را به شکل زیر محاسبه کرد:

${\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\,f(x)\,dx.}$

چند روش محاسبه

از روش‌های بدست آوردن تابع چگالی احتمالی متغیر تصادفی X مشتق‌گیری از تابع توزیع تجمعی (F_X(x آن است و که به صورت زیر تعریف می‌شود

${\displaystyle x\to F_{X}(x)=\operatorname {P} (X\leq x)}$

${\displaystyle {\frac {d}{dx}}F(x)=f(x).}$

یک روش دیگر برای بدست آوردن تابع چگالی احتمالی متغیر تصادفی X تخمین مقدار آن در یک بازه کوچک مانند ${\displaystyle [x,x+\varepsilon ]}$: است.

${\displaystyle \Pr(x<X<x+\varepsilon )=f(t)\,\varepsilon .}$

یا به عبارت دیگر

${\displaystyle \lim _{\varepsilon \to 0}P(x<X<x+\varepsilon )/\varepsilon }$:

رابطه بین توزیع‌های گسسته و پیوسته

می‌توان بعضی از متغیرهای تصادفی گسسته را نیز با استفاده از تابع چگالی احتمالی توصیف کرد. به‌طور مثال برای متغیر تصادفی که دو مقدار ۱ و -۱ را هر کدام با احتمال ۱/۲ می‌گیرد، می‌توان چگالی احتمال زیر را نسبت داد

${\displaystyle f(t)={\frac {1}{2}}(\delta (t+1)+\delta (t-1)).}$

به‌طور کلی اگر متغیر تصادفی n مقدار حقیقی را اختیار کند می‌توان تابع چگالی احتمال آن را به این شکل نوشت

${\displaystyle f(t)=\sum _{i=1}^{n}p_{i}\,\delta (t-x_{i}),}$

که مقادیر x₁, …, x_n مقادیری هستند که متغیر تصادفی X با احتمال p₁, …, p_n اختیار می‌کند..

چگالی احتمال توابع چندمتغیره

برای متغیرهای تصادفی ${\displaystyle x_{1},\ldots ,x_{n}}$ همچنین می‌توان یک تابع چگالی چندمتغیره تعریف کرد که به تمامی "${\displaystyle X}$"ها بستگی داشته باشد که به آن تابع چگالی احتمال مشترک (توأم) گویند. این تابع چگالی تابع چگالی ${\displaystyle n}$ متغیره نام دارد به‌طوری‌که به ازای هر فضای احتمال "${\displaystyle n}$" بعدی "${\displaystyle D}$" از متغیرهای تصادفی ${\displaystyle x_{1},\ldots ,x_{n}}$ احتمال اینکه این دسته متغیرها در "${\displaystyle D}$" قرار بگیرند، به صورت زیر است:

${\displaystyle \Pr \left(X_{1},\ldots ,X_{N}\in D\right)=\int _{D}f_{X_{1},\dots ,X_{N}}(x_{1},\ldots ,x_{N})\,dx_{1}\cdots dx_{N}.}$

اگر(F(x₁, …, x_n) = Pr(X₁ ≤ x₁, …, X_n ≤ x_n باشد، به آن توزیع تجمعی احتمال بردار (X₁, …, X_n) گوییم که در آن صورت توزیع چگالی احتمال توأم از طریق مشتق‌گیری از آن بدست می‌آید:

${\displaystyle f(x)={\frac {\partial ^{n}F}{\partial x_{1}\cdots \partial x_{n}}}{\bigg |}_{x}}$

چگالی توزیع حاشیه‌ای

(f_Xi(x_i به ازای i=۱، ۲، …,n چگالی توزیع حاشیه‌ای می‌گوییم که فقط تابع X_i است. می‌توان آن را از طریق انتگرال‌گیری از توزیع تجمعی نسبت به n-1 متغیر دیگر بدست آورد.

${\displaystyle f_{X_{i}}(x_{i})=\int f(x_{1},\ldots ,x_{n})\,dx_{1}\cdots dx_{i-1}\,dx_{i+1}\cdots dx_{n}.}$

استقلال

تابع توزیع مشترک n متغیره X₁, …, X_n مستقل از تک تک آن‌ها مستقل است اگر و تنها اگر:

${\displaystyle f_{X_{1},\dots ,X_{n}}(x_{1},\ldots ,x_{n})=f_{X_{1}}(x_{1})\cdots f_{X_{n}}(x_{n}).}$

نتیجه فرعی

اگر بتوان تابع توزیع مشترک یک بردار n تایی را به صورت حاصلضرب n تابع تک متغیره نوشت

${\displaystyle f_{X_{1},\dots ,X_{n}}(x_{1},\ldots ,x_{n})=f_{1}(x_{1})\cdots f_{n}(x_{n}),}$

(لزومی ندارد که هر f_i یک چگالی احتمال باشد) در آن صورت n متغیر از یکدیگر مستقل هستند و چگالی توزیع احتمال هریک به صورت زیر محاسبه می‌شود:

${\displaystyle f_{X_{i}}(x_{i})={\frac {f_{i}(x_{i})}{\int f_{i}(x)\,dx}}.}$

مثال

این مثال ابتدایی حالت ساده دو متغیره از تعریف تابع چکالی احتمال چند متغیره است. فرض کنید فضای ${\displaystyle {\vec {R}}}$ یک فضای دو متغیره با بردار مختصات (X, Y) است. احتمال اینکه ${\displaystyle {\vec {R}}}$ در کنج مثبت باشد، اینگونه است:

${\displaystyle \Pr \left(X>0,Y>0\right)=\int _{0}^{\infty }\int _{0}^{\infty }f_{X,Y}(x,y)\,dx\,dy.}$

جمع دو متغیر تصادفی مستقل

تابع چگالی احتمال دو متغیر مستقل U و V، که هر یک دارای یک تابع چگالی احتمالند، کانولوشن تابع چگالی تک تک آن هاست:

${\displaystyle f_{U+V}(x)=\int _{-\infty }^{\infty }f_{U}(y)f_{V}(x-y)\,dy=\left(f_{U}*f_{V}\right)(x)}$

می‌توان رابطه بالا را به N متغیر مستقل، با چگالی‌های U₁, …, U_N تعمیم داد:

${\displaystyle f_{U_{1}+\ldots +U_{N}}(x)=\left(f_{U_{1}}*\ldots *f_{U_{N}}\right)(x)}$

متغیرهای وابسته و تغییر متغیر

اگر تابع چگالی احتمال متغیر تصادفی X به صورت (f_X(x داده شده باشد، می‌توان (ولی معمولاً غیرضروری است، زیر را مشاهده کنید) تابع چگالی احتمال متغیری مانند (Y = g(X را محاسبه کرد. به این کار «تغییر متغیر» می‌گویند و در عمل برای تولید متغیر تصادفی با شکل دلخواه f_g(X) = f_Y با استفاده از مولد عدد تصادفی شناخته شده (برای مثال یکنواخت)، مورد استفاده قرار می‌گیرد.

اگر تابع g یکنواخت باشد، در آن صورت تابع چگالی حاصل به صورت زیر است:

${\displaystyle f_{Y}(y)=\left|{\frac {1}{g'(g^{-1}(y))}}\right|\cdot f_{X}(g^{-1}(y)).}$

در اینجا منظور از g⁻¹، تابع معکوس و منظور از 'g، تابع مشتق است.

این به دنبال این حقیقت ناشی می‌شود که احتمال در ناحیه مشتق‌گیری تحت تأثیر تغییر متغیر، باید ثابت بماند. یعنی:

${\displaystyle \left|f_{Y}(y)\,dy\right|=\left|f_{X}(x)\,dx\right|,}$

یا

${\displaystyle f_{Y}(y)=\left|{\frac {dx}{dy}}\right|f_{X}(x)=\left|{\frac {1}{g'(x)}}\right|f_{X}(x)=\left|{\frac {1}{g'(g^{-1}(y))}}\right|f_{X}(g^{-1}(y)).}$

برای توابعی که یکنواخت نیستند، تابع چگالی احتمال "y" به صورت زیر است:

${\displaystyle \sum _{k=1}^{n(y)}\left|{\frac {1}{g'(g_{k}^{-1}(y))}}\right|\cdot f_{X}(g_{k}^{-1}(y))}$

که در آن (n(y تعداد جواب‌های "x" برای رابطه g(x) = y و (g⁻¹_k(yها همان جواب‌ها هستند.

حال وسوسه انگیز است که در مورد امید ریاضی((E(g(X نیز بیندیشیم. به این منظور ابتدا باید چگالی احتمال(f_g(X را برای متغیر تصادفی جدید (Y = g(X بیابیم. به جای محاسبه

${\displaystyle E(g(X))=\int _{-\infty }^{\infty }yf_{g(X)}(y)\,dy,}$

بهتر است.

${\displaystyle E(g(X))=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx.}$

را محاسبه کرد.

دو انتگرال در تمامی شرایط در حالی که X و (g(X دارای تابع توزیع چگالی باشند، جواب یکسانی دارند. هیچ الزامی وجود ندارد که تابع g یک تابع یک به یک باشد. برخی مواقع انتگرال دوم، بسیار راحت تر از اولی قابل محاسبه است.

متغیرهای چندگانه

فرمول بالا را می‌توان به متغیرهایی (که آن‌ها را دوباره y می‌نامیم) وابسته به چند متغیر تصادفی تعمیم داد. (f(x₀, x₁, …, x_m−1 را می‌توان به عنوان تابع چگالی احتمال y در نظر گرفت که به آن‌ها وابسته است که این وابستگی به صورت y = g(x₀, x₁, …, x_m−1) است. در نتیجه تابع چگالی به صورت زیر بدست می‌آید:

${\displaystyle \int \limits _{y=g(x_{0},x_{1},\dots ,x_{m-1})}{\frac {f(x_{0},x_{1},\dots ,x_{m-1})}{{\sqrt {\sum _{j=0}^{j<m}}}({\frac {\partial g}{\partial x_{j}}}(x_{0},x_{1},\dots ,x_{m-1}))^{2}}}\;dV}$

که در آن انتگرال روی m-1 بعد است و باید dV را متناسب با این انتگرال جایگزین کرد. متغیرهای تصادفی x₀, x₁, …, x_m−1 بالطبع توابعی از این پارامتریزه کردن‌ها هستند.

شاید بصری به نظر برسد، ولی این ناشی از مطلب زیر است: فرض کنید 'x' یک متغیر تصادفی n-بعدی با تابع چگالی احتمال f است. اگر y = H(x) و H تابعی دوسویه و تشخیص پذیر باشد، y دارای چگالی احتمال g است:

${\displaystyle g(\mathbf {y} )=f(\mathbf {x} )\left\vert \det \left({\frac {d\mathbf {x} }{d\mathbf {y} }}\right)\right\vert }$

که مشتق در نظر گرفته شده، ماتریس ژاکوبی معکوس تابع H نسبت به y است.

با استفاده از تابع دلتا، (و فرض بر استقلال) جواب یکسانی به صورت زیر بدست می‌آید.

اگر تابع چگالی احتمال متغیرهای تصادفی مستقل X_i, i = ۱, ۲, …n به صورت (f_Xi(x_i داده شده باشند، می‌توان تابع چگالی احتمال متغیرهایی مانند (Y = G(X₁, X₂, …X_n را حساب کرد. فرمول زیر ارتباطی بین تابع چگالی احتمال y که با (f_Y(y نشان می‌دهیم و (f_Xi(x_i با استفاده از تابع دلتای دیراک برقرار می‌کند:

${\displaystyle f_{Y}(y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ldots \int _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(x_{2})\ldots f_{X_{n}}(x_{n})\delta (y-G(x_{1},x_{2},\ldots x_{n}))\,dx_{1}\,dx_{2}\,\ldots dx_{n}}$

منابع

1. Grinstead, Charles M.; Snell, J. Laurie (2009). "Conditional Probability - Discrete Conditional" (PDF). Grinstead & Snell's Introduction to Probability. Orange Grove Texts. ISBN 1-61610-046-X. Retrieved 2019-07-25.
2. Probability distribution function PlanetMath بایگانی‌شده در ۲۰۱۱-۰۸-۰۷ توسط Wayback Machine

• مشارکت‌کنندگان ویکی‌پدیا. «Markov chain». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۶ ژوئیهٔ ۲۰۱۲.
• مشارکت‌کنندگان ویکی‌پدیا. «Probability density». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۸ ژوئیهٔ ۲۰۱۲.

• Probability and Statistics in Engineering And Management Science, William W. Hines, Douglas C. Montgomery, Third Edition, John Wiley and Sons, 1990, ISBN 0-471-60090-3.