توابع وابسته لژاندر

در ریاضیات، چندجمله ای‌های وابسته لژاندر جواب‌های متعارف:

${\displaystyle (1-x^{2}){\frac {d^{2}}{dx^{2}}}P_{\ell }^{m}(x)-2x{\frac {d}{dx}}P_{\ell }^{m}(x)+\left[\ell (\ell +1)-{\frac {m^{2}}{1-x^{2}}}\right]P_{\ell }^{m}(x)=0,}$

از معادله زیر موسوم به معادله لژاندر هستند:

${\displaystyle {\frac {d}{dx}}\left[(1-x^{2}){\frac {d}{dx}}P_{\ell }^{m}(x)\right]+\left[\ell (\ell +1)-{\frac {m^{2}}{1-x^{2}}}\right]P_{\ell }^{m}(x)=0}$

که در آن شاخص ℓ و m (که اعداد صحیح هستند) به عنوان مرتبه و درجه چند جمله ای لژاندر وابسته می‌باشند. این معادله دارای جواب‌های غیر صفر است و تنها در صورتی در [1, 1−] غیر منفردند که اعداد صحیح ℓ و m در شرط ${\displaystyle 0\leq \left|{m}\right\vert \leq \left|{\ell }\right\vert }$ صدق کنند. هنگامی که شاخص m زوج باشد، این تابع یک چند جمله ای است. هنگامی که m برابر صفر و ℓ مقداری صحیح باشد، این توابع با چندجمله ای‌های لژاندر معادلند. به‌طور کلی هرگاه ℓ و m اعداد صحیح هستند، راه حل‌ها معمولاً به عنوان «چندجمله ای‌های لژاندر وابسته» خوانده می‌شود، حتی زمانی که m مقداری فرد بوده و معادله یک چندجمله ای نباشد. به‌طور کلی رده عمومی این توابع با مقادیر واقعی یا مرکب دلخواه از ℓ و m توابع لژاندر هستند. در این حالت پارامترها معمولاً با حروف یونانی برچسب گذاری می‌شوند.

معادله دیفرانسیل معمولی لژاندر اغلب در فیزیک و سایر زمینه‌های فنی کاربرد دارد، به ویژه در زمان حل معادله لاپلاس (و معادلات دیفرانسیل با مشتقات جزئی وابسته) در مختصات کروی. توابع وابسته لژاندر نقشی حیاتی در تعریف هماهنگ‌های کروی دارد.

تعریف برای پارامترهای صحیح و غیر منفی ℓ و m

این توابع به صورت ${\displaystyle P_{\ell }^{m}(x)}$ که در آن بالانویس نشان دهنده ترتیب تابع است، و نه توان P. در تعریف دقیق تر، آن‌ها تعیین‌کننده مرتبه مشتق چندجمله‌ای‌های لژاندر هستند. (m ≥ ۰)

${\displaystyle P_{\ell }^{m}(x)=(-1)^{m}(1-x^{2})^{m/2}{\frac {d^{m}}{dx^{m}}}\left(P_{\ell }(x)\right)}$،

توابع توصیف شده در این معادله با مقادیر مشخص شده از پارامترهای ℓ و m معادله دیفرانسیل عمومی لژاندر را برآورده می‌کنند. پاسخ معادله لژاندر Pℓ با تفکیک m به شرح زیر است:[1]

${\displaystyle (1-x^{2}){\frac {d^{2}}{dx^{2}}}P_{\ell }(x)-2x{\frac {d}{dx}}P_{\ell }(x)+\ell (\ell +1)P_{\ell }(x)=0.}$

علاوه بر این، بر طبق فرمول رودریگز داریم:

${\displaystyle P_{\ell }(x)={\frac {1}{2^{\ell }\,\ell$ !}}\ {\frac {d^{\ell }}{dx^{\ell }}}\left[(x^{2}-1)^{\ell }\right],}

که P_ℓ^m را می‌توان به صورت زیر تعریف کرد:

${\displaystyle P_{\ell }^{m}(x)={\frac {(-1)^{m}}{2^{\ell }\ell$ !}}(1-x^{2})^{m/2}\ {\frac {d^{\ell +m}}{dx^{\ell +m}}}(x^{2}-1)^{\ell }.}

این معادله گستره m را به ℓ ≤ m ≤ ℓ− محدود می‌کند. طبق تعریف P_ℓ^±m، حاصل عبارت فوق با جایگزینی m±، متناسب است. ضمن اینکه ضرایب توان در دو طرف معادله باید برابر باشد.

${\displaystyle {\frac {d^{\ell -m}}{dx^{\ell -m}}}(x^{2}-1)^{\ell }=c_{lm}(1-x^{2})^{m}{\frac {d^{\ell +m}}{dx^{\ell +m}}}(x^{2}-1)^{\ell },}$

که از آن نتیجه می‌دهد ثابت تناسب برابر است با

${\displaystyle c_{lm}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}},}$

بطوری که

${\displaystyle P_{\ell }^{-m}(x)=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}(x).}$

نمادگذاری جایگزین

نمادگذاری زیر نیز در نوشته‌ها استفاده می‌شود:[2]

${\displaystyle P_{\ell m}(x)=(-1)^{m}P_{\ell }^{m}(x)}$

تعامد

با فرض ${\displaystyle 0\leq {m}\leq {\ell }}$، این توابع شرط تعامد را به ازای مقدار ثابت m برآورده می‌کنند:

${\displaystyle \int _{-1}^{1}P_{k}^{m}P_{\ell }^{m}dx={\frac {2(\ell +m)!}{(2\ell +1)(\ell -m)!}}\ \delta _{k,\ell }}$

که در آن δ_{k, ℓ} همان تابع دلتای کرونیکر است.

همچنین، این توابع شرط تعامد را به ازای مقدار ثابت ℓ نیز برآورده می‌کنند:

${\displaystyle \int _{-1}^{1}{\frac {P_{\ell }^{m}P_{\ell }^{n}}{1-x^{2}}}dx={\begin{cases}0&{\mbox{if }}m\neq n\\{\frac {(\ell +m)!}{m(\ell -m)!}}&{\mbox{if }}m=n\neq 0\\\infty &{\mbox{if }}m=n=0\end{cases}}}$

مقادیر منفی m و/یا ℓ

این معادله دیفرانسیل نسبت به تغییر علامت m کاملاً ناوردا است.

این توابع برای مقادیر منفی m همانگونه که در بالا نشان داده شدبرابر با مقادیر مثبت m هستند:

${\displaystyle P_{\ell }^{-m}=(-1)^{m}{\frac {(\ell -m)!}{(\ell +m)!}}P_{\ell }^{m}}$

(این رابطه حاصل تعریف فرمول رودریگز است. این تعریف همچنین نشان می‌دهد که روابط بازگشتی مختلف برای مقادیر مثبت یا منفی m برقرار است.)

${\displaystyle {\textrm {If}}\quad {\mid }m{\mid }>\ell \,\quad \mathrm {then} \quad P_{\ell }^{m}=0.\,}$

این معادله دیفرانسیل همچنین تحت تغییر از ℓ تا ℓ − 1 − ناوردا است، و تابع برای مقادیر منفی ℓ به صورت زیر تعریف می‌شود

${\displaystyle P_{-\ell }^{m}=P_{\ell -1}^{m},\ (\ell =1,\,2,\,...)}$.

پاریته

طبق تعریف تأیید می‌شود که توابع وابسته لژاندر هم زوج یا فرد می‌شوند، بطوری که

${\displaystyle P_{\ell }^{m}(-x)=(-1)^{\ell +m}P_{\ell }^{m}(x)}$

چند گزینه نخست از توابع وابسته لژاندر

توابع وابسته لژاندر به ازای m = ۰

توابع وابسته لژاندر به ازای m = ۱

توابع وابسته لژاندر به ازای m = ۲

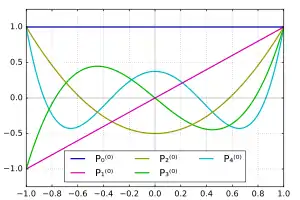
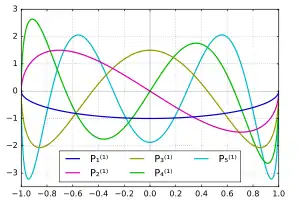
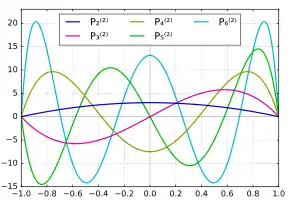
چند گزینه اول از توابع وابسته لژاندر، که شامل مقادیر منفی m نیز می‌باشند، عبارتند از:

${\displaystyle P_{0}^{0}(x)=1}$

${\displaystyle P_{1}^{-1}(x)=-{\begin{matrix}{\frac {1}{2}}\end{matrix}}P_{1}^{1}(x)}$

${\displaystyle P_{1}^{0}(x)=x}$

${\displaystyle P_{1}^{1}(x)=-(1-x^{2})^{1/2}}$

${\displaystyle P_{2}^{-2}(x)={\begin{matrix}{\frac {1}{24}}\end{matrix}}P_{2}^{2}(x)}$

${\displaystyle P_{2}^{-1}(x)=-{\begin{matrix}{\frac {1}{6}}\end{matrix}}P_{2}^{1}(x)}$

${\displaystyle P_{2}^{0}(x)={\begin{matrix}{\frac {1}{2}}\end{matrix}}(3x^{2}-1)}$

${\displaystyle P_{2}^{1}(x)=-3x(1-x^{2})^{1/2}}$

${\displaystyle P_{2}^{2}(x)=3(1-x^{2})}$

${\displaystyle P_{3}^{-3}(x)=-{\begin{matrix}{\frac {1}{720}}\end{matrix}}P_{3}^{3}(x)}$

${\displaystyle P_{3}^{-2}(x)={\begin{matrix}{\frac {1}{120}}\end{matrix}}P_{3}^{2}(x)}$

${\displaystyle P_{3}^{-1}(x)=-{\begin{matrix}{\frac {1}{12}}\end{matrix}}P_{3}^{1}(x)}$

${\displaystyle P_{3}^{0}(x)={\begin{matrix}{\frac {1}{2}}\end{matrix}}(5x^{3}-3x)}$

${\displaystyle P_{3}^{1}(x)=-{\begin{matrix}{\frac {3}{2}}\end{matrix}}(5x^{2}-1)(1-x^{2})^{1/2}}$

${\displaystyle P_{3}^{2}(x)=15x(1-x^{2})}$

${\displaystyle P_{3}^{3}(x)=-15(1-x^{2})^{3/2}}$

${\displaystyle P_{4}^{-4}(x)={\begin{matrix}{\frac {1}{40320}}\end{matrix}}P_{4}^{4}(x)}$

${\displaystyle P_{4}^{-3}(x)=-{\begin{matrix}{\frac {1}{5040}}\end{matrix}}P_{4}^{3}(x)}$

${\displaystyle P_{4}^{-2}(x)={\begin{matrix}{\frac {1}{360}}\end{matrix}}P_{4}^{2}(x)}$

${\displaystyle P_{4}^{-1}(x)=-{\begin{matrix}{\frac {1}{20}}\end{matrix}}P_{4}^{1}(x)}$

${\displaystyle P_{4}^{0}(x)={\begin{matrix}{\frac {1}{8}}\end{matrix}}(35x^{4}-30x^{2}+3)}$

${\displaystyle P_{4}^{1}(x)=-{\begin{matrix}{\frac {5}{2}}\end{matrix}}(7x^{3}-3x)(1-x^{2})^{1/2}}$

${\displaystyle P_{4}^{2}(x)={\begin{matrix}{\frac {15}{2}}\end{matrix}}(7x^{2}-1)(1-x^{2})}$

${\displaystyle P_{4}^{3}(x)=-105x(1-x^{2})^{3/2}}$

${\displaystyle P_{4}^{4}(x)=105(1-x^{2})^{2}}$

رابطه بازگشتی

این توابع دارای تعدادی روابط بازگشتی اند:

${\displaystyle (\ell -m+1)P_{\ell +1}^{m}(x)=(2\ell +1)xP_{\ell }^{m}(x)-(\ell +m)P_{\ell -1}^{m}(x)}$

${\displaystyle 2mxP_{\ell }^{m}(x)=-{\sqrt {1-x^{2}}}\left[P_{\ell }^{m+1}(x)+(\ell +m)(\ell -m+1)P_{\ell }^{m-1}(x)\right]}$

${\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}P_{\ell }^{m}(x)={\frac {-1}{2m}}\left[P_{\ell -1}^{m+1}(x)+(\ell +m-1)(\ell +m)P_{\ell -1}^{m-1}(x)\right]}$

${\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}P_{\ell }^{m}(x)={\frac {-1}{2m}}\left[P_{\ell +1}^{m+1}(x)+(\ell -m+1)(\ell -m+2)P_{\ell +1}^{m-1}(x)\right]}$

${\displaystyle {\sqrt {1-x^{2}}}P_{\ell }^{m}(x)={\frac {1}{2\ell +1}}\left[(\ell -m+1)(\ell -m+2)P_{\ell +1}^{m-1}(x)-(\ell +m-1)(\ell +m)P_{\ell -1}^{m-1}(x)\right]}$

${\displaystyle {\sqrt {1-x^{2}}}P_{\ell }^{m}(x)={\frac {1}{2\ell +1}}\left[-P_{\ell +1}^{m+1}(x)+P_{\ell -1}^{m+1}(x)\right]}$

${\displaystyle {\sqrt {1-x^{2}}}P_{\ell }^{m+1}(x)=(\ell -m)xP_{\ell }^{m}(x)-(\ell +m)P_{\ell -1}^{m}(x)}$

${\displaystyle {\sqrt {1-x^{2}}}P_{\ell }^{m+1}(x)=(\ell -m+1)P_{\ell +1}^{m}(x)-(\ell +m+1)xP_{\ell }^{m}(x)}$

${\displaystyle {\sqrt {1-x^{2}}}{\frac {d}{dx}}{P_{\ell }^{m}}(x)={\frac {1}{2}}\left[(\ell +m)(\ell -m+1)P_{\ell }^{m-1}(x)-P_{\ell }^{m+1}(x)\right]}$

${\displaystyle (1-x^{2}){\frac {d}{dx}}{P_{\ell }^{m}}(x)={\frac {1}{2\ell +1}}\left[(\ell +1)(\ell +m)P_{\ell -1}^{m}(x)-\ell (\ell -m+1)P_{\ell +1}^{m}(x)\right]}$

${\displaystyle (x^{2}-1){\frac {d}{dx}}{P_{\ell }^{m}}(x)={\ell }xP_{\ell }^{m}(x)-(\ell +m)P_{\ell -1}^{m}(x)}$

${\displaystyle (x^{2}-1){\frac {d}{dx}}{P_{\ell }^{m}}(x)=-(\ell +1)xP_{\ell }^{m}(x)+(\ell -m+1)P_{\ell +1}^{m}(x)}$

${\displaystyle (x^{2}-1){\frac {d}{dx}}{P_{\ell }^{m}}(x)={\sqrt {1-x^{2}}}P_{\ell }^{m+1}(x)+mxP_{\ell }^{m}(x)}$

${\displaystyle (x^{2}-1){\frac {d}{dx}}{P_{\ell }^{m}}(x)=-(\ell +m)(\ell -m+1){\sqrt {1-x^{2}}}P_{\ell }^{m-1}(x)-mxP_{\ell }^{m}(x)}$

اولین روابط بازگشتی:

${\displaystyle P_{\ell +1}^{\ell +1}(x)=-(2\ell +1){\sqrt {1-x^{2}}}P_{\ell }^{\ell }(x)}$

${\displaystyle P_{\ell }^{\ell }(x)=(-1)^{\ell }(2\ell -1)!!(1-x^{2})^{(\ell /2)}}$

${\displaystyle P_{\ell +1}^{\ell }(x)=x(2\ell +1)P_{\ell }^{\ell }(x)}$

پارامتربندی زاویه ای

این توابع زمانی که متغیر از نوع زاویه ای لحاظ می‌شود بسیار مفیدند، مانند ${\displaystyle x=\cos \theta }$:

${\displaystyle P_{\ell }^{m}(\cos \theta )=(-1)^{m}(\sin \theta )^{m}\ {\frac {d^{m}}{d(\cos \theta )^{m}}}\left(P_{\ell }(\cos \theta )\right)\,}$

با استفاده از رابطه ${\displaystyle (1-x^{2})^{1/2}=\sin \theta }$، چند نمونه از لیست ذکر شده در بالا، به عنوان اولین چند جمله ای‌های وابسته لژاندر به صورت زیر تبدیل می‌شوند:

${\displaystyle {\begin{aligned}P_{0}^{0}(\cos \theta )&=1\\[8pt]P_{1}^{0}(\cos \theta )&=\cos \theta \\[8pt]P_{1}^{1}(\cos \theta )&=-\sin \theta \\[8pt]P_{2}^{0}(\cos \theta )&={\tfrac {1}{2}}(3\cos ^{2}\theta -1)\\[8pt]P_{2}^{1}(\cos \theta )&=-3\cos \theta \sin \theta \\[8pt]P_{2}^{2}(\cos \theta )&=3\sin ^{2}\theta \\[8pt]P_{3}^{0}(\cos \theta )&={\tfrac {1}{2}}(5\cos ^{3}\theta -3\cos \theta )\\[8pt]P_{3}^{1}(\cos \theta )&=-{\tfrac {3}{2}}(5\cos ^{2}\theta -1)\sin \theta \\[8pt]P_{3}^{2}(\cos \theta )&=15\cos \theta \sin ^{2}\theta \\[8pt]P_{3}^{3}(\cos \theta )&=-15\sin ^{3}\theta \\[8pt]P_{4}^{0}(\cos \theta )&={\tfrac {1}{8}}(35\cos ^{4}\theta -30\cos ^{2}\theta +3)\\[8pt]P_{4}^{1}(\cos \theta )&=-{\tfrac {5}{2}}(7\cos ^{3}\theta -3\cos \theta )\sin \theta \\[8pt]P_{4}^{2}(\cos \theta )&={\tfrac {15}{2}}(7\cos ^{2}\theta -1)\sin ^{2}\theta \\[8pt]P_{4}^{3}(\cos \theta )&=-105\cos \theta \sin ^{3}\theta \\[8pt]P_{4}^{4}(\cos \theta )&=105\sin ^{4}\theta \end{aligned}}}$

روابط متعامدی که در بالا ذکر شد، در این فرمول آمده‌است: برای مقدار ثابت m, ${\displaystyle P_{\ell }^{m}(\cos \theta )}$ به ازای پارامتر θ در بازه ${\displaystyle [0,\pi ]}$${\displaystyle \sin \theta }$:

${\displaystyle \int _{0}^{\pi }P_{k}^{m}(\cos \theta )P_{\ell }^{m}(\cos \theta )\,\sin \theta \,d\theta ={\frac {2(\ell +m)!}{(2\ell +1)(\ell -m)!}}\ \delta _{k,\ell }}$

همچنین، به ازای ℓ ثابت:

${\displaystyle \int _{0}^{\pi }P_{\ell }^{m}(\cos \theta )P_{\ell }^{n}(\cos \theta )\csc \theta \,d\theta ={\begin{cases}0&{\text{if }}m\neq n\\{\frac {(\ell +m)!}{m(\ell -m)!}}&{\text{if }}m=n\neq 0\\\infty &{\text{if }}m=n=0\end{cases}}}$

در ازای θ، ${\displaystyle P_{\ell }^{m}(\cos \theta )}$ جواب‌های معادله زیر است

${\displaystyle {\frac {d^{2}y}{d\theta ^{2}}}+\cot \theta {\frac {dy}{d\theta }}+\left[\lambda -{\frac {m^{2}}{\sin ^{2}\theta }}\right]\,y=0\,}$

به عبارت دقیق تر، با توجه به صحیح بودن ${\displaystyle 0\leq {m}}$، معادله فوق تنها زمانی دارای پاسخ‌های نامعمول خواهد بود که رابطه ${\displaystyle \lambda =\ell (\ell +1)\,}$ برای هر ℓ صحیح بزرگتر از m صدق کند، و این پاسخ‌ها متناسبند با ${\displaystyle P_{\ell }^{m}(\cos \theta )}$.

منابع

1. [[#CITEREF|]].
2. الگو:Abramowitz Stegun ref

• Arfken, G.B.; Weber, H.J. (2001), Mathematical methods for physicists, Academic Press, ISBN 0-12-059825-6; Section 12.5. (Uses a different sign convention.)
• Belousov, S. L. (1962), Tables of normalized associated Legendre polynomials, Mathematical tables, 18, Pergamon Press.
• Condon, E. U.; Shortley, G. H. (1970), The Theory of Atomic Spectra, Cambridge, England: Cambridge University Press, OCLC 5388084; Chapter 3.
• Courant, Richard; Hilbert, David (1953), Methods of Mathematical Physics, Volume 1, New York: Interscience Publischer, Inc.
• Dunster, T. M. (2010), "Legendre and Related Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248
• Edmonds, A.R. (1957), Angular Momentum in Quantum Mechanics, Princeton University Press, ISBN 0-691-07912-9; Chapter 2.
• Hildebrand, F. B. (1976), Advanced Calculus for Applications, Prentice Hall, ISBN 0-13-011189-9.
• Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248
• Schach, S. R. (1973) New Identities for Legendre Associated Functions of Integral Order and Degree, Society for Industrial and Applied Mathematics Journal on Mathematical Analysis, 1976, Vol. 7, No. 1: pp. 59–69

پیوند به بیرون

• Associated Legendre polynomials in MathWorld
• Legendre polynomials in MathWorld