دستگاه مختصات کروی

در ریاضیات، دستگاه مختصات کروی یک دستگاه مختصات برای نمایش حساب‌ها و اعداد هندسی در فضای سه بعدی با استفاده از سه مختصه است: فاصلهٔ شعاعی یک نقطه از یک مبدأ ثابت(${\displaystyle \rho }$)، زاویهٔ سمت‌الرأس (zenith angle) از قسمت مثبت محور z(اصطلاحاً فی) و زاویهٔ گرایی (azimuth angle) از قسمت مثبت محور x(اصطلاحاً تتا).

نقطه‌ای که با دستگاه مختصات کروی نمایش داده شده‌است

مشخصات

دستگاه مختصات کروی، دستگاه مختصاتی با سه مختصه‌است:

• مختصه ${\displaystyle \rho }$ (یا ${\displaystyle r}$) که روی کره‌های هم مرکز حول مبدأ است.
• مختصه ${\displaystyle \theta }$ روی مخروط‌های دوار قائم حول محور ${\displaystyle z}$ با راس واقع در مبدأ.
• مختصه ${\displaystyle \phi }$ که روی نیم صفحاتی که از محور قطبی ${\displaystyle z}$ می‌گذرد.

در فیزیک بنا به سنت جای ${\displaystyle \theta }$ و ${\displaystyle \phi }$ معکوس است یعنی ${\displaystyle \theta }$ زاویه با محور ${\displaystyle z}$ است.

محدوده مختصات

سه مختصه در محدوده‌های زیر می‌توانند باشند:

• مختصه ${\displaystyle \rho }$ (یا ${\displaystyle r}$):

${\displaystyle 0\leq \rho }$

• مختصه زاویه قطبی ${\displaystyle \theta }$:

${\displaystyle 0\leq \theta \leq 2\pi }$

• مختصه زاویه سمتی ${\displaystyle \phi }$:

${\displaystyle 0\leq \phi \leq \pi }$

رابطه با مختصات دکارتی

مختصات دستگاه کروی را با استفاده از روابط زیر به دستگاه مختصات دکارتی می‌توان تبدیل کرد:

• برای مختصه ${\displaystyle \rho }$:

${\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}}}$

• برای مختصه زاویه قطبی ${\displaystyle \theta }$:

${\displaystyle {\theta }=\arctan \left({\frac {y}{x}}\right)}$

• برای مختصه زاویه سمتی ${\displaystyle \phi }$:

${\displaystyle {\phi }=\arccos \left({\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\right)}$

مختصات دکارتی نیز را با روابط زیر می‌توان به دستگاه مختصات کروی برد:

• مختصه ${\displaystyle x}$:

${\displaystyle {x}=\rho \,\sin \phi \,\cos \theta \quad }$

• مختصه ${\displaystyle y}$:

${\displaystyle {y}=\rho \,\sin \phi \,\sin \theta \quad }$

• مختصه ${\displaystyle z}$:

${\displaystyle {z}=\rho \,\cos \phi \quad }$

حساب برداری

• بردار ${\displaystyle A}$ در مختصات کروی به صورت زیر نمایش داده می‌شود:

${\displaystyle {\overrightarrow {A}}=A_{r}{\boldsymbol {\hat {r}}}+A_{\theta }{\boldsymbol {\hat {\theta }}}+A_{\phi }{\boldsymbol {\hat {\phi }}}}$

• ضرب داخلی و ضرب خارجی بردارها مانند تمامی دستگاه‌های مختصّات متعامد به همان فرمولبندی دستگاه مختصات دکارتی انجام می‌شود.
• گرادیان تابع اسکالر ${\displaystyle f}$ به صورت زیر است:

${\displaystyle \nabla f={\partial f \over \partial r}{\boldsymbol {\hat {r}}}+{1 \over r}{\partial f \over partial\theta }{\boldsymbol {\hat {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \phi }{\boldsymbol {\hat {\phi }}}}$

• واگرایی بردار ${\displaystyle A}$:

${\displaystyle \nabla \cdot \mathbf {A} ={1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\phi } \over \partial \phi }}$

• کرل بردار ${\displaystyle A}$ در دستگاه کروی:

${\displaystyle \nabla \times \mathbf {A} ={1 \over r\sin \theta }\left({\partial \over \partial \theta }(A_{\phi }\sin \theta )-{\partial A_{\theta } \over \partial \phi }\right){\boldsymbol {\hat {r}}}+{1 \over r}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \phi }-{\partial \over \partial r}\left(rA_{\phi }\right)\right){\boldsymbol {\hat {\theta }}}+{1 \over r}\left({\partial \over \partial r}\left(rA_{\theta }\right)-{\partial A_{r} \over \partial \theta }\right){\boldsymbol {\hat {\phi }}}}$

• عملگر لاپلاس بر روی ${\displaystyle f}$ در مختصات کروی:

${\displaystyle \Delta f=\nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \phi ^{2}}}$

تبدیل‌های دستگاه مختصات

دستگاه مختصات جغرافیایی

دستگاه مختصات جغرافیایی بک مدل دیگر از دستگاه مختصات کروی است که کاربرد اصلی آن در جغرافیا است اما در ریاضیات و فیزیک نیز استفاده‌هایی دارد. در جغرافی، ρ معمولاً حذف یا با مقداری که ارتفاع یا بلندی از سطح دریا را نشان می‌دهد جایگزین می‌شود.

عرض جغرافیایی ${\displaystyle {\delta }\,}$، مکمل سمت‌الرأس یا متمم عرض جغرافیایی است و می‌تواند با این روابط تبدیل شود:

${\displaystyle {\delta }=90^{\circ }-\phi }$

یا

${\displaystyle {\phi }=90^{\circ }-\delta }$

با این وجود عرض جغرافیایی عمدتاً با φ نیز نمایش داده می‌شود. این، یک زاویه سمت‌الرأس را که از صفحهٔ xy سرچشمه می‌گیرد با دامنهٔ ‎ -۹۰° ≤ φ ≤ ۹۰° ‏ بیان می‌کند. طول جغرافیایی به وسیلهٔ درجه به شرق یا به غرب از °۰ اندازه‌گیری می‌شود، بنابراین دامنه‌اش ‎ -۱۸۰° ≤ θ ≤ ۱۸۰° ‏ است.

دیفرانسیل‌ها

بردار واحد در مختصات کروی

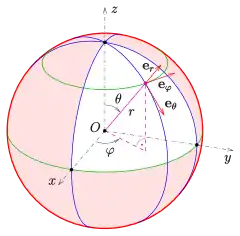
المان خط برای جابه جایی بینهایت کوچک از (r, θ, φ) به (r + dr, θ + dθ, φ + dφ)برابر است با:

• دیفرانسیل خطی:

${\displaystyle d\mathbf {l} =dr\mathbf {\hat {r}} +rd\theta {\boldsymbol {\hat {\theta }}}+r\sin \theta d\phi {\boldsymbol {\hat {\phi }}}}$

• دیفرانسیل سطحی:

${\displaystyle d\mathbf {S} =r^{2}\sin \phi d\theta d\phi \mathbf {\hat {r}} +r\sin \phi drd\phi {\boldsymbol {\hat {\theta }}}+rdrd\theta {\boldsymbol {\hat {\phi }}}}$

• دیفرانسیل حجمی:

${\displaystyle dv=r^{2}\sin \phi drd\theta d\phi \,}$

جستارهای وابسته

• دستگاه مختصات خمیده خط
• دستگاه مختصات دکارتی
• دستگاه مختصات استوانه‌ای
• دستگاه مختصات قطبی
• کُره

منابع

• جورج براون آرفکن، روشهای ریاضی در فیزیک، ترجمهٔ اعظم پورقاضی، مرکز نشر دانشگاهی، شابک &#۸۲۰۶;۹۶۴-۰۱-۰۹۱۴-۲ مقدار |شابک= را بررسی کنید: invalid character (کمک)

• Wikipedia contributors, "Spherical coordinate system," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Spherical_coordinate_system&oldid=172958916 (accessed November 22, 2007).