دستگاه مختصات استوانهای
مختصات استوانهای نوعی مختصات متعامد (عمود برهم) است که در آن یک نقطه، در فضا بر روی قاعدهٔ یک استوانه در نظر گرفته میشود. مکان آن نقطه بر اساس شعاع و ارتفاع استوانه (r و z) و زاویهای که شعاع قاعده گذرنده از آن نقطه با محور x میسازد (θ)، بیان میشود. این دستگاه، در حالت دوبعدی، با حذف مختص z به مختصات قطبی تبدیل میشود. در فیزیک و به ویژه در مباحث الکترومغناطیس و مخابرات به جای r، θ،z به ترتیب از حروف ρ، φ،z استفاده میشود.
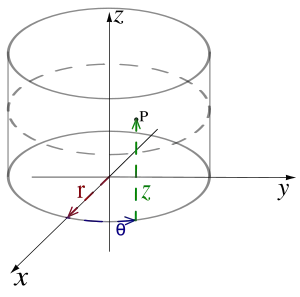
استوانه
رویهای که ترسیم آن و نوشتن h(x,y)=c معرکه
دستگاه مختصات استوانهای
ممکن است معادله یک رویه در یکی از دستگاههای سادهتر از معادله آن در دستگاه دکارتی باشد. در چنین مواردی استفاده از دستگاه مناسب باعث صرفه جویی در وقت میشود. این موضوع در حل انتگرالهای چندگانه اهمیت بیشتری پیدا میکند. همانطور که میدانید حل برخی انتگرالهای سهگانه در دستگاه دکارتی گاهی غیرممکن میباشد، ولی با یک تغییر مختصات ساده به راحتی میتوانیم به جواب مورد نظر برسیم. در دستگاه مختصات استوانهای، استوانههایی که محورشان در امتداد محور z هستند معادلات بسیار سادهای دارند. این دستگاه مختصات در فضا از طریق تلفیق مختصات قطبی در صفحه xy با محور z معمولی به دست میآید. به این ترتیب به هر نقطه در فضا یک یا چند سه تایی مختصات به صورت (r,θ،z) نسبت داده میشود. در فیزیک و به ویژه در مباحث الکترومغناطیس و مخابرات به جای r ،θ ،z به ترتیب از حروف ρ، φ،z استفاده میشود.
در واقع توسط روابط فوق میتوان یک نقطه در دستگاه مختصات دکارتی را به دستگاه مختصات استوانهای منتقل کرد. در مختصات استوانهای معادله r=a فقط دایرهای در صفحه xy را مشخص نمیکند بلکه استوانهای کامل حول محور z را توصیف میکند. خود محور z با معادله r=0 معین میشود. معادله θ=θ۰ توصیفکننده صفحهای است که شامل محور z است و زاویهای به اندازه θ۰ رادیان با قسمت مثبت محور x میسازد. چند رابطه که مختصات دکارتی، استوانهای و کروی را به هم مربوط میسازند.
پیوند به بیرون
منابع
- ریاضیات مهندسی پیشرفته کریزیک
- فیزیک هالیدی