جمعکننده با قابلیت پیشبینی رقم نقلی
جمعکننده با قابلیت پیشبینی بیت نقلی(به انگلیسی: A carry-lookahead adder) و بهطور خلاصه CLA، نوعی مدار جمعکننده است که در مدارات منطقی به کار میرود. این مدار با کاهش زمان مورد نیاز برای تولید بیت نقلی سرعت جمع زدن را افزایش میدهد. در مقابل این نوع جمعکننده گونهٔ دیگری از مدار جمعکننده وجود دارد که با نام جمعکننده با بیت نقلی پلهای (در بعضی متون ترجمه شده به فارسی جمعکننده با بیت نقلی موج گونه) معروف است(به انگلیسی: Ripple Carry Adder). هرچند که جمعکننده با بیت نقلی پلهای از لحاظ اجزای مداری ساده تراز جمعکننده با پیشبینی بیت نقلی میباشد اما از لحاظ سرعت انجام عملیات کندتر است چراکه در این گونه از جمعکنندهها مدار لازم است منتظر بماند تابیت نقلی حاصل از جمع دو بیت قبلی محاسبه شده و آنگاه برای محاسبه بیت نقلی حاصل از جمع دو بیت بعدی اقدام کند.[1] چارلز بابیج خطای تحمیل شده بر عملکرد مدار در اثر رقم نقلی پلهای را کشف کرد و در ماشینهای محاسباتی خویش، ساز وکاری راجهت پیشبینی رقم نقلی توسعه داد. جرالد روزنبرگ از شرکت IBM حق اختراع یک جمعکننده دودویی با پیشبینی رقم نقلی را برای خود در سال ۱۹۵۷ ثبت نمود.
تئوری کار
یک جمعکننده با بیت نقلی پلهای در جمع زدن از همان روشی استفاده میکند که یک انسان با استفاده از قلم و کاغذ انجام میدهد. از سمت راستترین (و در واقع کم ارزش ترین) رقم شروع کرده و دو رقم متناظر با هم جمع میشوند و حاصل جمع بدست میآید. ممکن است که در این مرحله یک رقم نقلی نیز تولید شود (به عنوان مثال در روش قلم و کاغذ حاصل جمع ۹ و ۵ برابر ۴ به همراه یک رقم نقلی ۱ خواهد بود). بر این اساس به غیر از سمت راستترین موقعیت مکانی، دردیگر مکانهای عددی باید رقم نقلی احتمالی ۱ که از سمت راست وارد میشود را نیز در محاسبه در نظر داشت. . این سخن بدین معناست که نمیتوان مقدار نهایی حاصل جمع دو رقم در یک موقعیت مکانی را بدون دانستن اینکه آیا هیچگونه رقم نقلی از سمت راست وجود دارد یا نه، بهطور قطع مشخص کرد. علاوه بر این چنانچه در روش قلم و کاغذ حاصل جمع بدون رقم نقلی ۹ بشود یا اینکه در محاسبات دودویی حاصل جمع بدون رقم نقلی برابر۱ بشود، حتی نمیتوان گفت که آیا در آن موقعیت مکانی، باید یک رقم نقلی به سمت چپ منتقل بشود یا خیر. بدترین حالت هنگامی است که نتیجه جمع یک رشته رقم متناظر در سیستم دهگانی به شکل ...۹۹۹۹۹.... یا در سیستم دودویی به شکل .....۱۱۱۱... در بیاید، چراکه در اینصورت تا زمانی که مقدار رقم نقلی وارد شده از سمت راست، در دست نباشد به هیچ عنوان نمیتوان نتیجه نهایی جمع را تعیین نمود و در واقع لازم است که رقم نقلی پس از هر بار ارزیابی به اندازه یک موقعیت مکانی به سمت چپ منتشر شود. بهطور مثال در سیستم دهگانی اگر رقم نقلی برابر ۱ باشد نتیجه جمع دیگر ۹ نیست بلکه ۹+۱=۰ با نقلی جدید ۱ است یا در سیستم دودویی نتیجه جمع با احتساب نقلی ورودی دیگر ۱ نیست بلکه ۱+۱=۰ با نقلی خروجی ۱ است. علت نامگذاری جمعکنندههای با بیت نقلی پلهای یا موج گونه به این نام آنست که در اینگونه جمعکنندهها، رقم نقلی مانند یک موج از راست به چپ منتشر میگردد که موجب کندی سرعت نیز میشود. به عنوان مثال در نظر بگیرید که بخواهید دو عدد صحیح ۳۲ بیتی را جمع بزنید در اینصورت رقم نقلی نهایی با عبور و انتشار رقمهای نقلی پیشین از بین تمامی ۳۲ جمعکننده تک بیتی موجود در جمعکننده، تولید خواهد شد.
پیشبینی رقم نقلی به دو چیز بستگی دارد:
- محاسبه کردن، برای هر موضع رقم، بایستی مشخص شود که آیا رقم نقلی برای پخش وجود دارد اگر یک رقم از سمت راست بیاید.
- ترکیب کردن این مقادیر محاسبه شده، تا بتوان سریعتر نتیجه گرفت که آیا در هر گروه از ارقام، یک رقم نقلی که از سمت راست میآید پخش میشود یا نه.
فرض کنید که یک گروه ۴ رقمی انتخاب شدهاست. سپس توالی وقوع اتفاقات چیزی مثل زیر میشود:
- تمامی جمعکنندههای ۱ بیتی نتایج خود را محاسبه میکنند. بهطور همزمان، واحدهای پیشبینیکننده نیز محاسبات خود را انجام میدهند.
- فرض کنید که نقل در گروه خاصی رخ میدهد. در طی حداکثر ۵ گیت تاخیر، بیت نقلی در انتهای سمت چپ گروه ظاهر شده و شروع به توزیع در میان گروه سمت چپ خودش میکند.
- اگر قرار باشد که بیت نقلی به توزیع خود ادامه داده و به گروه بعد از خودش نیز پخش شود، واحد پیشبینی انتقال از قبل این استنباط را داشتهاست. طبق آن، قبل از اینکه بیت نقلی از گروه بعدی مشتق شود، واحد پیشبینی فوراً (در طی ۱ گیت تأخیر) قادر است بگوید که گروه بعدی سمت چپ که بیت نقلی را دریافت خواهد کرد کدام است، و در همان زمان، میتواند واحد پیشبینی بعدی سمت چپ خودش که بیت نقل در راه رسیدن به آن است، را بگوید.
اثر خالص این است که نقلها با توزیع و پخش آرام در بین هر یک از ۴ بیت گروه شروع شده، همانند سیستم نقل موجی؛ اما ناگهان سرعت آن ۴ برابر میشود، از یک واحد پیشبینی نقل به بعدی جهش پیدا میکند. نهایتاً، در هر گروهی که بیت نقلی را دریافت میکند، نقل به صورت کند در بین رقمهای آن گروه پخش میشود. هر چه تعداد بیتهای یک گروه بیشتر باشد، منطق پیشبینی رقم نقل پیچیده تر میشود، و در «مسیر کند» داخل هر یک از گروهها نسبت به «مسیر سریع» بین گروهها، زمان بیشتری صرف میشود (که توسط منطق پیشبینی رقم نقلی مهیا میگردد). از طرف دیگر، هر چه تعداد بیتهای داخل یک گروه کمتر باشد، گروههای بیشتری به صورت عرضی کنار هم وجود خواهد داشت که از یک سر خود به سمت دیگر عدد نقلی را دریافت میکند، و در نتیجه تسریع کمتری در عملیات حاصل میشود. تصمیمگیری در مورد سایز گروههایی که توسط منطق پیشبینی رقم نقلی اداره شود، مستلزم تجزیه و تحلیل مفصل گیت و تأخیرهای توزیع (پخش) برای تکنولوژی خاص مورد استفاده، میباشد. امکان داشتن بیشتر از یک سطح از منطق پیشبینی بیت نقلی وجود دارد، و در حقیقت معمولاً چنین عمل میشود. هر واحد پیشبینی رقم نقلی یک سیگنال تولید میکند که به آن «اگر بیت نقلی از سمت راست بیاید، من آن را به سمت چپ توزیع خواهم کرد»، و این سیگنالها را میتوان با هم ترکیب کرد، به طوری که هر یک از گروههای (بگذار بگوییم) متشکل از چهار واحد پیشبینی رقم نقلی بخشی از یک «ابر گروه» میشوند که در مجموع ۱۶ بیت از اعداد اضافه شونده را اداره میکنند. منطق پیشبینی رقم نقلی «اَبَر گروه» قادر خواهد بود که پیشبینی کند که آیا رقم نقلی وارده به ابر گروه (فرا گروه) در سراسر آن پخش خواهد شد، و با استفاده از این اطلاعات، قادر به پخش رقم نقلی از راست به چپ به مقدار ۱۶ برابر سریعتر از رقم نقلی موجی بومی خواهد بود. با این نوع اجرای دو سطحی، رقم نقلی ممکن است ابتدا در «مسیر کند» جمعکننده منفرد پخش شده، سپس با رسیدن به انتهای سمت چپ گروه، از طریق «مسیر سریع» منطق پیشبینی رقم نقلی ۱۶ بیتی به سرعت پخش شود. مجدداً ذکر میشود که سایزهایی که برای گروه انتخاب میشود به جزئیات حقیقی سرعت پخش شدن سیگنالها در درون گیتهای منطقی و از یک گیت منطقی به دیگری، بستگی دارد. در گروههای با تعداد بزرگ (صدها یا حتی هزاران بیت) منطق پیشبینی رقم نقلی بیشتر از این پیچیده نمیشود، زیرا لایههای بیشتری از ابر گروه و ابر ابرگروه در صورت ضرورت اضافه میشود. اضافه شدن تعداد گیتها نیز بهطور متوسط است. اگر تمامی گروهها دارای سایز ۴ باشند، به یک سوم کل واحدهای پیشبینی رقم نقلی نسبت به تعداد جمعکنندهها میرسیم. هرچند، «مسیر کند» بر سر راه سطوح سریعتر بر کل سیستم تاخیری اعمال میکند (برای نمونه، یک جمعکننده ۲۵۶ بیتی میتواند تا حداکثر ۲۴ گیت تأخیر در فرایند حمل و نقل خود داشته باشد)، و خود انتقال فیزیکی سیگنال از یک سر عدد بزرگ به سر دیگر مشکل اصلی خواهد بود. در این سایزها، جمعکنندههای نقل-ذخیره ارجحیت دارند، از آنجایی که زمانی برای توزیع و پخش رقم نقلی در کل مصرف نمیکنند.
روش پیش بینی رقم نقلی
در منطق پیشبینی رقم نقلی از مفاهیم انتقال تولیدی و انتشاری استفاده میشود. هرچند در زمینه جمعکننده پیشبینی رقم نقلی، طبیعی تر این است که تولید و انتشار را در زمینه جمع باینری تصور کنیم، این مفاهیم را میتوان بهطور عمومی تری نیز استفاده نمود. در توصیف زیر، کلمه رقم را میتوان با بیت جایگزین کرد زمانی که به جمع باینری اشاره دارد. جمع دو ورودی ۱ رقمی A و B همیشه تولیدی است اگر جمع همیشه به صورت نقلی باشد، صرفنظر از اینکه نقل ورود وجود داشته باشد یا نه (بطور هم ارز، صرف نظر از اینکه رقم کم ارزش تر نیز در جمع رقم نقلی وجود دارد یا نه). برای مثال، در جمع دهگانی ۵۲+۶۷، جمع رقم دهگان ۵ و ۶ تولیدی است، زیرا نتیجه آن یک رقم صدگان را نقل میکند صرفنظر از اینکه رقم یکان نقل شود یا نه (در این مثال، رقم یکان نقل نمیشود (۹=۷+۲)). در موارد جمع باینری، A+B تولیدی است اگر و تنها اگر هر دوی A و B مقدار ۱ باشد. اگر ما بنویسیم G(A,B) که نمایانگر پیشبینی باینری است که در صورت صحیح است که اگر و تنها اگر A+B تولیدی باشد، در نتیجه ما داریم:
G (A, B) = A. B
زمانی جمع دو ورودی ۱ رقمی A و B انتشاری گفته میشود که جمع در صورت وجود رقم نقلی رخ دهد (بطور هم ارز، زمانی که رقم کم ارزش تر بعدی در جمع رقم نقلی محسوب شود). برای مثال، در جمع دهگانی ۳۷+۶۲، جمع کردن رقمهای دهگان ۳ و ۶ انتشاری است زیرا نتیجه آن فقط زمانی به رقم صدگان پخش و منتشر میشود که یک منتقل شود (که در این مثال، رقم یکان چنین نیست). توجه شود که انتشار و تولید در رابطه با رقم منفرد در جمع تعیین میشود و به سایر رقمهای موجود در جمع بستگی ندارد. در جمع باینری، A+B انتشاری است اگر و تنها اگر حداقل یکی از A یا B برابر ۱ باشد. اگر ما بنویسیم P(A,B) که دلالت بر پیشبینی باینری دارد که زمانی و تنها زمانی صحیح است که A+B انتشاری باشد، بنابراین خواهیم داشت:
P (A, B) = A + B
گاهی اوقات تعریف نسبتاً متفاوتی از انتشار استفاده میشود. طبق این تعریف A+B گفته میشود که انتشاری است اگر جمع زمانی انجام شود که یک رقم نقلی وجود داشته باشد، اما اگر رقم نقلی موجود نباشد، جمع صورت نمیگیرد. خوشبختانه، به علت شیوه استفاده از بیتهای تولیدی و انتشاری توسط منطق پیشبینی بیت نقلی، مهم نیست که کدام تعریف استفاده شود. در زمان جمع باینری، این تعریف به صورت زیر بیان میشود:
P' (A, B) = A ⊕ B
در جبر باینری، or از xor سریعتر است و اجرای ترانزیستور کمتری را در یک جمعکننده پیشبینی بیت نقلی چند-سطحی به خود میگیرد، بنابراین سادهتر این است که از P' (A, B) استفاده شود. با در نظر گرفتن مفاهیم تولید و انتشار، چه موقع رقم جمع نقل میشود؟ دقیقاً زمانی نقل میشود که یا جمع یک or تولید کند یا بیت کم ارزش تر بعدی منتقل شود و جمع انتشار یابد. این مطلب در جبر بولی بدین شکل است، با Ci که بیت رقم i را منتقل میکند و Pi و Gi که بیتهای رقم i را به ترتیب منتشر و تولید میکنند، داریم:
جزئیات اجرایی (پیادهسازی)
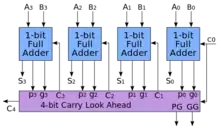
برای هر بیتی در یک توالی باینری که بایستی جمع زده شود، منطق پیشبینی بیت نقلی تعیین میکند که آیا آن جفت بیت نقلی را تولید یا نقلی را منتشر میکنند یا نه. این به مدار امکان را میدهد که دو عددی که قرار است با هم جمع شوند را «پیش-پردازش» کند و از قبیل بیت نقلی را پیشبینی کند. سپس زمانی که جمع واقعی صورت میگیرد، تأخیری برای اثر نقل موجی صرف نخواهد شد (یا زمانی که طول میکشد تا بیت نقلی از اولین جمعکننده گذشته و به آخرین جمعکننده کامل برسد). در زیر یک مدار پیشبینی بیت نقلی تعمیم دهی شده ۴ بیتی ساده نشان داده شدهاست که با ۴ بیت جمعکننده بیت نقلی موجی استفاده شد در بعضی از تعدیلهای فوق، ترکیب شدهاست: برای مثال، منطق تولید (g) و انتشار (p) در زیر آمده است. توجه شود که مقادیر عددی تعیینکننده سیگنالی هستند که از مدار بالا میآید، از صفر شروع شده و در انتهای چپ صفر بوده و در انتهای سمت راست ۳ است.
C1 = G0 + P0. C0
C2 = G1 + P1. C1
C3 = G2 + P2. C2
C4 = G3 + P3. C3
جایگزین کردن C1 در C2، سپس C2 در C3، سپس C3 در C4 موجب حصول بسط معادلات میشود:
C1 = G0 + P0. C0
C2 = G1 + G0. P1 + C0. P0. P1
C3 = G2 + G1. P2 + G0. P1. P2 + C0. P0. P1. P2
C4 = G3 + G2. P3 + G1. P2. P3+ G0. P1. P2. P3 + C0. P0. P1. P2. P3
برای تعیین اینکه آیا یک جفت بیت نقلی را تولید میکنند، کارهای منطقی پیگیری میشوند:
Gi = Ai. Bi
برای تعیین اینکه آیا یک جفت بیت نقلی را منتشر میکنند، یکی از عبارات منطقی زیر پیگیری میشود:
Pi = Ai ⊕ Bi
Pi = Ai + Bi
دلیل زمینهای این کار براساس ارزیابی C1 = G0 + P0. C0 میباشد. تنها تفاوت در واقعیت جداول بین (A ⊕ B) و (A + B) میباشد زمانی که هر دوی A و B یک هستند. هر چند اگر هر دوی A و B یک باشند، سپس مقدار G0 نیز ۱ میشود (از آنجایی که معادله به صورت A.B است)، و P0. C0 نامربوط میشوند. معمولاً از xor بین مدارهای جمعکننده کامل استفاده میشود، اما OR نیز یک گزینه بدیل دیگر است (فقط برای پیشبینی بیت نقلی) که خیلی سادهتر از وضعیت شمارش ترانزیستور است. جمعکننده پیشبینی بیت نقلی ۴ بیتی را میتوان در مدارهای سطح بالاتر نیز استفاده کرد که برای هر کدام یک مدار منطقی CLA طراحی میشود که سیگنالهای تولید و انتشار را برای مدار منطقی CLA رده بالاتر ایجاد نماید. انتشار گروهی (PG) و تولید گروهی (GG) برای CLA چهار بیتی به صورت زیر خواهد شد:
PG = P0. P1. P2. P3
GG = G3 + G2. P3 + G1. P3. P2 + G0. P3. P2. P1
با کنار هم قرار دادن چهار CLA 4 بیتی، چهار گروه انتشاری و چهار گروه تولیدی حاصل میشود. یک واحد پیشبینی بیت نقلی (LCU) این ۸ مقدار را گرفته و از منطق یکسانی برای محاسبه Ci در CLAها استفاده میکند. سپس LCU ورودی نقلی را برای هر یک از چهار CLA و پنجمی که مساوی C16 است، تولید میکند. محاسبه تأخیر گیت جمعکننده ۱۶ بیت (با استفاده از 4 CLA و یک LCU) به اندازه جمعکننده نقلی موجی راحت نیست. از نقطه زمانی صفر شروع میشود:
• در زمان ۱ محاسبه Pi و Gi انجام میشود.
- در زمان ۳ محاسبه Ci انجام میشود.
- در زمان ۲ محاسبه PG انجام میشود.
- در زمان ۳ محاسبه GG انجام میشود
• محاسبه ورودیهای CLAها از LCU به صورت زیر است:
o زمان ۰ برای اولین CLA o زمان ۵ برای دومین، سومین، و چهارمین CLA
- محاسبه Si به صورت زیر انجام میشود
o زمان ۴ برای اولین CLA o زمان ۸ برای دومین، سومین، و چهارمین CLA
- محاسبه آخرین بیت نقلی (C16) در زمان ۵ انجام میشود.
بیشترین زمان ۸ تاخیر گیت میباشد (برای S [8-15]). یک جمعکننده نقل موجی ۱۶ بیت به خود ۳۱ تاخیر گیت میگیرد.
زنجیره بیت نقلی منچستر
زنجیره نقل منچستر گونهای از جمعکننده پیشبینی بیت نقلی است که از منطق اشتراکی برای کم کردن شمارش ترانزیستوری استفاده میکند. همانطور که در بخش اجرا و پیادهسازی در بالا دیدیم، منطق تولیدی هر نقل حاوی تمامی منطقهای مورد استفاده برای تولید نقل قبلی است. زنجیره نقل منچستر ناقلهای واسطهای را توسط محصور کردن گرهها در گیتی که مهمترین مقادیر نقلی را محاسبه میکند، تولید میکند. هرچند همه اعضای خانواده منطقی دارای این گرهها نیستند، یک مثل مهم آن CMOS است. منطق پویا میتواند از منطق اشتراکی حمایت کند، همانطور که از منطق گیت انتقال حمایت میکند. یکی از مشکلات اصلی زنجیره نقل منچستر این ست که بار ظرفیتی تمامی این خروجیها را به خود میگیرد، که با هم مقاومتی در ترانزیستورها تولید میشود که منجر به تأخیر در انتشار میشود تا هر چه جمعکننده با قابلیت پیشبینی بیت نقلی(به انگلیسی: A carry-lookahead adder) و بهطور خلاصه CLA، نوعی مدار جمعکننده است که در مدارات منطقی به کار میرود. این مدار با کاهش زمان مورد نیاز برای تولید بیت نقلی سرعت جمع زدن را افزایش میدهد. در مقابل این نوع جمعکننده گونهٔ دیگری از مدار جمعکننده وجود دارد که با نام جمعکننده با بیت نقلی پلهای معروف است(به انگلیسی: Ripple Carry Adder) و بهطور خلاصه RCA. هرچند که جمعکننده با بیت نقلی پلهای از لحاظ اجزای مداری ساده تراز جمعکننده با پیشبینی بیت نقلی میباشد اما از لحاظ سرعت انجام عملیات کندتر است چراکه در این گونه از جمعکنندهها مدار لازم است منتظر بماند تابیت نقلی حاصل از جمع دو بیت قبلی محاسبه شده و آنگاه برای محاسبه بیت نقلی حاصل از جمع دو بیت بعدی اقدام کند.[1] اما جمعکننده با پیشبینی بیت نقلی میتواند پیش از آنکه عمل جمع کردن هر دو بیت متناظر را انجام دهد بیتهای نقلی مورد نیاز آن دو را محاسبه کرده و در اختیار بگذارد و در نتیجه زمان انتظار برای تولید رقم نقلی مورد نیاز در جمع بیتهای با ارزش بالاتر کاهش مییابد.