حدس اردوش–فابر–لوواس
حدس اردوش–فابر–لوواس (به انگلیسی: Erdős–Faber–Lovász conjecture) یک مسئله بسیار عمیق و مهم در بحث رنگ آمیزی گرافها در نظریه گرافها است.
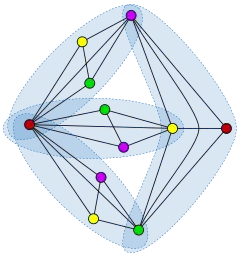
این نظریه بیان میکند که: اجتماع k کپی از k دسته که هر ۲ دستهٔ متمایز دلخواه حداکثر در یک راس اشتراک دارند دارای عدد رنگی k است. حداد و تاردیف در سال ۲۰۰۴ این نظریه را به بیان دیگری و با مطرح کردن یک مثال از کمیتههای موجود در دانشگاه ارائه کردند: فرض کنید در یک دانشکدهٔ دانشگاه k کمیته وجود دارد و هر کدام هم شامل k نفر از اعضای هیئت علمی هستند و قرار است که همهٔ کمیتهها در یک اتاق با هم جلسه داشته باشند که در اتاق k صندلی وجود دارد. همچنین فرض کنید که اشتراک هر ۲ کمیتهٔ متمایز دلخواه شامل ۱ نفر میشود. آیا ممکن است که اعضای کمیتهها را به صندلیهایی نسبت دهیم بهطوریکه هر عضو در همه کمیتههایی که عضو آنها است روی صندلی ثابتی بنشیند؟
پال اردوش ابتداً مبلغ ۵۰ دلار برای اثبات این حدس به عنوان جایزه قرار داده بود ولی بعداً آن را به مبلغ ۵۰۰ دلار افزایش داد.[1] بهترین نتیجهٔ یافته شده تا به امروز این است که عدد رنگی این مسئله حداکثر [2] است.
اگر مسئله را راحتتر و با شرایط کمتری در نظر بگیریم، بدین صورت که اجازه دهیم دستهها در هر چند راسی که میخواهند، اشتراک داشته باشند؛ آنگاه عدد رنگی این نوع گرافها حداکثر خواهد شد.[3]
جستارهای وابسته
پانویس
- چانگ و گراهام (۱۹۹۸).
- کان (۱۹۹۲).
- اردوس(۱۹۹۱)؛ هوراک و توزا (۱۹۹۰).
منابع
«Erdős–Faber–Lovász conjecture." Wikipedia, The Free Encyclopedia. 25 May 2008, 22:06 UTC. Wikimedia Foundation, Inc. 5 Jul 2008 <http://en.wikipedia.org/w/index.php?title=Erdős–Faber–Lovász_conjecture&oldid=214918375>.