خم درجه چهارم لوروت

در ریاضیات، خم درجه چهارم لوروت(به انگلیسی: Lüroth quartic) یک خم صفحه‌ای ناتکین از درجۀ چهار است که رأس‌های یک ستاره کامل را در بر می‌گیرد. این خم‌ها به افتخار ریاضی‌دان آلمانی، یاکوب لوروت، که نخستین بار آن‌ها را کشف کرد و به نامِ او خوانده می‌شود. در سال ۱۹۱۹، فرانک مورلی ثابت کرد که خم‌های لوروت یک زیرمجموعۀ باز از یک ابررویه درجۀ ۵۴ تشکیل می‌دهند که آن را «ابررویه لوروت»[1] نام نهاد که در فضای پیمانه‌ای[2] خم‌های درجۀ چهار یعنی، جای می‌گیرد.[3] بنینگ و بوتمر در سال ۲۰۱۱ نشان دادند که فضای پیمانه‌ای خم‌های لوروت گویا است.[4]

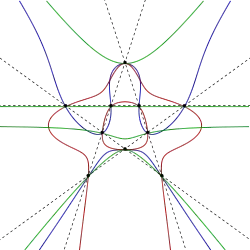
نمونه‌ای از یک خم لوروت

پانویس
  1. Lüroth hypersurface
  2. moduli space
  3. Morley, Frank (1919), "On the Lüroth Quartic Curve", American Journal of Mathematics (The Johns Hopkins University Press) 41 (4): 279–282
  4. Böhning, Christian; von Bothmer, Hans-Christian (2011), "On the rationality of the moduli space of Lüroth quartics", Mathematische Annalen (Springer Berlin / Heidelberg): 1–9,

منابع
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.