درخت جستجوی سه‌تایی

درخت جستجوی سه تایی در علوم رایانه، نوعی درخت پیشوندی است با این تفاوت که گره‌ها در حالت مشابه با درخت جستجوی دودویی قرار گرفته‌اند، اما دارای سه فرزند هستند. مانند تمام درخت‌های پیشوندی، یک درخت جستجوی سه تایی به عنوان داده ساختار آرایه انجمنی با توانایی جستجوی رشته می‌تواند استفاده شود. از کاربردهای متداول درخت جستجوی سه تایی می‌توان غلط یاب و تکمیل خودکار را نام برد.

درخت جستجوی سه‌تایی
نوع درخت
پیچیدگی زمانی
بر حسب نماد اوی بزرگ
میانگین بدترین حالت
فضا ‎ ‎
جستجو O(log n)‎ O(n)‎
درج O(log n)‎ O(n)‎
حذف O(log n)‎ O(n)‎

توضیحات
مثالی از درخت جستجوی سه تایی

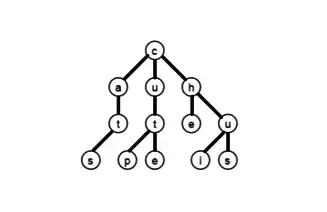
همانند درخت دودویی که هر گره آن دارای یک مقدار و دو اشاره گر به زیردرختان اش است (زیر درخت اولی دارای عناصر کوچکتر از مقدار عنصر پدر و زیر درخت دومی دارای عناصر بزرگتر از از مقدار پدر) هر گره از یک درخت جستجوی سه تایی نیز شامل یک کاراکتر و سه اشاره گر به زیر درخت‌های اول، دوم و زیردرخت سوم می‌باشد که با نام‌های فرزند کوچکتر، فرزند مساوی و فرزند بزرگتر شناخته می‌شوند. یک گره همچنین می‌تواند اشاره گری به گره پدرش داشته باشد یا شاخصی که مشخص کند آیا به آخر کلمه رسیدیم یا نه.[1] اشاره گر فرزند کوچکتر به گره‌ای دارای کاراکتر کوچکتر از پدرش اشاره می‌کند همچنین اشاره گر فرزند بزرگتر به گره‌ای دارای کاراکتر بزرگتر از پدرش اشاره می‌کند اما اشاره گر فرزند مساوی به گره‌ای دارای کاراکتر بعدی در کلمه اشاره می‌کند.[2] شکل مقابل درخت جستجوی سه تایی شامل رشته‌های "as" و "at" و "cup" و "cute" و "he" و "i" و "us" را نشان می‌دهد:

همان‌طور که در شکل مشاهده می‌کنیم هر گره در درخت جستجوی سه تایی نشان دهنده یک کاراکتر از رشته ذخیره شده می‌باشد. همه رشته‌ها در زیر درخت وسط یک گره با آن پیشوند شروع می‌شود.

عملیات

جستجو

در رویه جستجو ما یک رشته داریم و هر مرحله از این پروسه گره مرتبط با رشته مفروض را پیدا می‌کنیم. روند جستجو با بررسی کردن گره ریشه آغاز می‌شود و مشخص می‌کند کدام یک از حالات زیر اتفاق می‌افتد. اگر اولین کاراکتر رشته از کاراکتر گره ریشه کمتر بود یک جستجوی بازگشتی با ریشه فرزند کوچکتر فراخوانی می‌شود. به طور مشابه اگر اولین کاراکتر رشته از کاراکتر گره ریشه بزرگتر بود یک جستجوی بازگشتی با ریشه فرزند بزرگتر فراخوانی می‌شود؛ و در نهایت اگر اولین کاراکتر رشته مساوی با کاراکتر گره ریشه بود و رشته کاراکتر بیشتری نداشت گره برگشت داده می‌شود اما اگر کاراکترهای دیگری در رشته وجود داشت کاراکتر اول را از رشته حذف می‌کنیم و یک جستجوی بازگشتی با ریشه فرزند مساوی فراخوانی می‌کنیم. روند جستجو را به صورت غیر بازگشتی نیز می‌توان نوشت که در آن از یک اشاره گری به گره فعلی و اشاره گر دیگری کخ به کاراکتر فعلی در رشته اشاره می‌کنند استفاده می‌کنیم.

درج

رویه درج در درخت جستجوی سه تایی همانند رویه جستجو به صورت بازگشتی تعریف می‌شود بدین صورت که همواره بر روی یکه از گره‌های درخت و کلیدی (رشته‌ای) که به تدریج در حال کوچکتر شدن است فراخوانی می‌شود. اگر این روند به گره‌ای برسد که هنوز ساخته نشده بود آن را می‌سازد و کاراکتر را به آن واگذار می‌کند. چه گره جدید ساخته شده باشد یا نه این روال بررسی می‌کند که مقدار کاراکتر کلید بزرگتر، مساوی یا کوچکتر از مقدار گره می‌باشد و در هرکدام از حالت‌ها یک فراخوانی مناسب انجام می‌دهد. اگر با این حال، کاراکتر اول کلید مساوی با مقدار گره باشد روند درج بر روی فرزند مساوی فراخوانی می‌شود و کاراکتر اول کلید حذف می‌شود. درخت جستجوی سه تایی مانند درخت دودویی و دیگر ساختمان داده‌ها می‌تواند بر اساس کلیدها منحط ساخته شود. درج کلیدهای مرتب یکی از راه‌های رسیدن به بدترین درخت فاسد است. درج کردن کلیدها به صورت رندم اغلب باعث تولید درخت متعادل می‌شود.

پیچیدگی زمانی

پیچیدگی زمانی درخت جستجوی سه تایی به طور قابل ملاحظه‌ای توسط ورودی‌ها تغییر می‌کند. همچنین درخت سه تایی وقتی ورودی‌ها رشته‌های مشابه باشند یا دارای پیشوند یکسانی باشند عملکرد بهتری دارد. متناوباً درخت جستجوی سه تایی هنگام ذخیره‌سازی تعداد زیادی رشته‌های کوچک مرتبط، مفید واقع خواهد شد (مانند لغات در یک فرهنگ لغت). پیچیدگی زمانی درخت جستجوی سه تایی همانند درخت جستجوی دودویی در زمان لگاریتمی انجام می‌شود، اما هنگامی که فاسد (بدترین حالت) باشد اردر زمانی آن خطی است.

پیچیدگی زمانی عملیات درخت جستجوی سه تایی:

Average-case running time Worst-case running time
LookUp (O(log n (O(n
Insertion (O(log n (O(n
Delete (O(log n (O(n

کاربردها

از درخت جستجوی سه تایی در حل بسیاری از مسایل که در آن تعداد زیادی رشته ذخیره و با ترتیب خاصی بازیابی می‌شود می‌توان استفاده کرد. چند کاربرد متداول یا اغلب مفید این درخت عبارت است از:

  • همیشه از ترای (درخت عبارت) می‌توان استفاده کرد اما داده ساختاری با مصرف حافظه کمتر ارجحیت دارد.
  • یک داده ساختار تند که فضای کمی مصرف می‌کند برای نگاشت رشته‌ها به داده‌های دیگر مورد استفاده قرار می‌گیرد.[3]
  • پیاده‌سازی تکمیل خودکار.
  • به عنوان غلط یاب.
  • جستجوی نزدیکترین همسایه (غلط یاب حالت خاص از این مورد است).
  • به عنوان پایگاه داده.
  • در مکان یک جدول درهم سازی.[3]

منابع
  1. «Ternary Search Trees». Dr. Dobb's. دریافت‌شده در ۲۰۱۶-۰۵-۰۸.
  2. «Efficient auto-complete with a ternary search tree». igoro.com. دریافت‌شده در ۲۰۱۶-۰۵-۰۸.
  3. Flint، Wally. «Plant your data in a ternary search tree». JavaWorld. بایگانی‌شده از اصلی در ۱۹ سپتامبر ۲۰۱۳. دریافت‌شده در ۲۰۱۶-۰۵-۰۸.

پیوند به بیرون
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.