الگوریتم جستجوی رشته

الگوریتم‌های جستجوی رشته (و یا تطبیق رشته‌ها) به رده‌ی مهمی از الگوریتم‌های موجود در رابطه با رشته‌ها اطلاق می‌شود. در این گونه از الگوریتم‌ها، مسئله‌ی اصلی پیدا کردن مکان‌های تکرار یک یا چند الگوی مورد جستجو (Pattern) در یک رشته‌ی بزرگ‌ (Text) است.

در این مثال، رشته‌ها از کنار هم گذاشتن تعدادی کاراکتر متعلق به یک مجموعه‌ی متناهی به نام الفبا (${\displaystyle \Sigma }$) ساخته می‌شوند. ${\displaystyle \Sigma }$ می‌تواند حروف الفبای معمولی (از A تا Z)، الفبای دودویی (${\displaystyle \{0,1\}}$) یا الفبای DNA (${\displaystyle \{A,C,G,T\}}$) باشد که بسته به محل و کاربرد مسئله، تعیین می‌شود.

شرایط انتخاب الگوریتم

در هر حالت از محیط اجرای الگوریتم و شرایط مسئله، باید این شرایط را به خوبی بررسی کرد و بهترین الگوریتم را برای پیاده‌سازی و استفاده برگزید. به عنوان مثال، ممکن است حالات زیر بر محیط مسئله حاکم باشد:

• طول رشته Text بلند و طول رشته‌های Pattern بسیار کوتاه باشد.
• طول رشته Text بلند و طول رشته‌های Pattern نیز بلند باشد.
• رشته‌های Pattern ثابت باشند و تکرار‌های آن‌ها در رشته‌های Text متفاوت به صورت مداوم پرسمان شود.
• رشته‌ی Text ثابت باشد و Pattern های مختلف در طول زمان پرسمان شوند.

برای گرفتن بهترین کارایی در هر یک از این شرایط، باید الگوریتم مشخصی را انتخاب کرد.

همچنین در نوعی از این مسئله، رشته‌های Pattern به صورت یک عبارت منظم داده می‌شوند، و باید جایگاه تمام زیررشته‌هایی که با آن عبارت منظم مطابق هستند به عنوان خروجی برگردانده‌شود.

طبقه بندی کلی

الگوریتم‌های جستجوی رشته به صورت کلی به سه دسته‌ی زیر تقسیم می‌شوند:

الگوریتم‌های جستجوی تک الگو

در جدول زیر، چند الگوریتم معروف ذکر شده و از نظر مرتبه‌ی زمانی و حافظه با هم مقایسه شده‌اند. (${\displaystyle m}$ طول الگو (Pattern)، ${\displaystyle n}$ طول رشته متن (Text) و ${\displaystyle k=|\Sigma |}$ برابر با تعداد حروف الفبا است)

نام الگوریتم	زمان پیش‌پردازش	زمان تطبیق	حافظه مورد نیاز
الگوریتم جستجوی ساده‌لوحانه	بدون پیش‌پردازش	${\displaystyle \Theta (mn)}$	بدون حافظه جانبی
الگوریتم رابین-کارپ	${\displaystyle \Theta (m)}$	در حالت میانگین ${\displaystyle \Theta (n+m)}$ در بدترین حالت ${\displaystyle \Theta ((n-m)m)\in O(mn)}$	${\displaystyle O(1)}$
الگوریتم کنوث-موریس-پرت (KMP)	${\displaystyle \Theta (m)}$	${\displaystyle \Theta (n)}$	${\displaystyle \Theta (m)}$
الگوریتم بویر-مور	${\displaystyle \Theta (m+k)}$	در بهترین حالت${\displaystyle \Omega ({\frac {n}{m}})}$ در بدترین حالت ${\displaystyle O(mn)}$	${\displaystyle \Theta (k)}$

الگوریتم‌های جست‌و‌جوی تعدادی متناهی الگو

• الگوریتم آهو-کوراسیک (تعمیم‌یافته‌ی الگوریتم KMP)
• الگوریتم تطابق رشته‌ Commentz-Walter (تعمیم‌یافته‌ی الگوریتم Boyer-Moore)
• الگوریتم رابین‌کارپ برای جست‌وجوی چندالگویی

الگوریتم‌های جست‌و‌جوی تعدادی نامتناهی الگو

در این نوع از الگوریتم‌ها، استراتژی‌ها و ایده‌های متنوعی برای تطابق الگوهای ورودی (که به شکل عبارت منظم یا زبان منظم داده می‌شوند) به کار گرفته می‌شود.

بررسی چند مورد از الگوریتم‌های معرفی شده

الگوریتم جستجوی رشته‌ی ساده‌لوحانه (Naïve string search algorithm)

آسان‌ترین و ناکارآمدترین راه برای آن‌که یک رشته و مکان آن را در یک متن پیدا کنیم، امتحان کردن یک به یک همه‌ی مکان‌هایی که آن رشته می‌تواند قرار بگیرد است. یعنی یک اشاره‌گر را به عنوان ابتدای الگو، روی متن جلو می‌بریم و بررسی می‌کنیم که آیا این اشاره‌گر، می‌تواند ابتدای یک تکرار از الگو در متن باشد یا خیر. برای این‌کار، کاراکترهای بعد از اشاره‌گر را دانه‌به‌دانه با الگو مقایسه می‌کنیم؛ در صورت عدم انطباق یکی از آن کاراکتر‌ها، مشخص می‌شود که اشاره‌گر در مکان فعلی نمی‌تواند نمایان‌گر یک تکرار برای رشته باشد، پس اشاره‌گر را یک واحد به جلو می‌بریم. و در صورتی تا انتهای مقایسه، هیچ تناقضی وجود نداشت، به این معنی است که اشاره‌گر به یک تکرار از الگو در متن اشاره می‌کند. [1]

شبه‌کد جستجوی رشته‌ی ساده‌لوحانه:

procedure NaiveStringMatcher (T,P)
begin
  n=length(T);
  m=length(P);
  for s=0 to n-m do
    if P[1...m]=T[s+1...s+m] then
      print ("Pattern occurs with shift" s);
end

این الگوریتم از مرتبه زمانی ${\displaystyle O(m(n-m+1))\in O(mn)}$ است (فرض می‌کنیم که در این شبه‌کد، عمل مقایسه‌ی زیررشته‌ها به صورت کاراکتر به کاراکتر انجام خواهد شد).

جستجو بر پایه پذیرنده‌ی متناهی معین (Deterministic Finite Automata)

پذیرنده متناظر با رشته‌ی MOMMY

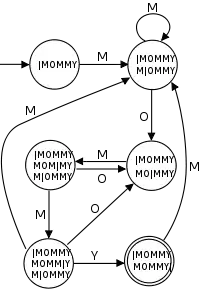
در این روش، ابتدا یک پذیرنده متناهی معین می‌سازیم که رشته‌هایی که حاوی الگوی مورد جستجوی ما هستند را بپذیرد؛ به این ترتیب که ابتدا یک زنجیره از State ها قرار می‌دهیم، که هر State نماینده‌ی یک مکان از الگو است (که تا آن‌جا روی الگو پیش رفته‌ایم). در واقع هر State نمایانگر یک پیشوند از الگو است. به غیر از یال‌های رو به جلو که با کاراکتر‌های متناظر الگو Label گذاری شده‌اند، هر State به‌ازای هر کاراکتر دیگر، به State ای قبل از خودش می‌رود. مثلاً State نماینده‌ی پیشوند ${\displaystyle S}$، با یال ${\displaystyle x}$ به State نماینده‌ی پیشوند ${\displaystyle P}$ می‌رود، اگر و تنها اگر ${\displaystyle P}$ بزرگ‌ترین پیشوندی از الگو باشد که برای ${\displaystyle Sx}$ پسوند است. همچنین رأس انتهایی متناظر با آخرین کاراکتر الگو، رأس پذیرش است.

با خواندن کاراکتر از رشته متن و حرکت روی این DFA، هر بار که به State پذیرش برسیم، یک تکرار از الگو را در متن پیدا کرده‌ایم. همچنین با تعمیم این روش، می‌توان الگوریتمی را برای جست‌وجوی عبارت‌های منظم در متن طراحی کرد.

البته هزینه ساخت چنین پذیرنده‌ای زیاد است (در صورت استفاده از ایده‌ی الگوریتم KMP، می‌توان با زمان ${\displaystyle O(m\Sigma )}$ این پذیرنده را ساخت) اما استفاده از آن سریع است.[2]

DFA شکل زیر برای تشخیص دادن واژه‌ی MOMMY استفاده شده‌است:

روش‌های مبتنی بر اندیس

این الگوریتم‌های جستجو متن را پیش‌پردازش می‌کنند؛ بعد از ساختن زیررشته اندیسی[3] (برای مثال درخت پسوندی یا آرایه پسوندی)، تعداد بارهایی که الگوی مورد جستجو در متن اتفاق افتاده‌است، به سرعت مشخص می‌شود؛ برای مثال یک درخت پسوندی را می‌توان در ${\displaystyle \Theta (m)}$ ساخت و همه‌ی z رخ‌داد الگوی مورد نظر در متن را می‌توان در ${\displaystyle \operatorname {O} (m+z)}$ پیدا کرد. این کار به سادگی با استفاده از یک بار جست‌و‌جوی عمق اول روی درخت پسوندی انجام می‌شود.

پیوند به بیرون

• دیکشنری انگلیسی به فارسی ساختمان داده و الگوریتم‌ها
• فهرست همه‌ی الگوریتم‌های جستجوی رشته‌

مراجع

1. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7
2. Kleinberg، Jon؛ Tardos، Éva. Algorithm Design. Pearson. شابک ۹۷۸۰۳۲۱۲۹۵۳۵۴.
3. Substring Index