پذیرنده متناهی معین

در نظریه اتوماتا، شاخه‌ای از علوم کامپیوتر نظری، ماشین‌های تعیین‌پذیر حالات متناهی (Deterministic finite-state machine) به آن دسته از ماشین‌های حالات متناهی اطلاق می‌شود که رشته متناهی از سمبل‌ها را می‌پذیرد یا رد می‌کند و برای هر رشته ورودی تنها محاسباتی یکتا از ماشین اتوماتا را تولید می‌کند. در واقع 'تعیین‌پذیری' در این ماشین‌ها به یکتایی محاسبات برمی‌گردد. در جستجوی ساده‌ترین روش‌ها برای نمایش ماشین‌های حالت متناهی، مک‌کالک (McCulloch) و پیتس (Pitts) در میان اولین محققانی بودند که مفاهیم و ایده‌هایی شبیه به ماشین‌های اتوماتای محدود را در سال ۱۹۴۳ معرفی کردند.

مثالی از یک ماشین تعین‌پذیر حالات متناهی که تنها اعدادی باینری را که مضربی از ۳ باشند، می‌پذیرد. در این‌جا حالت S₀ نیز هم حالت آغازین و هم حالت نهایی است.

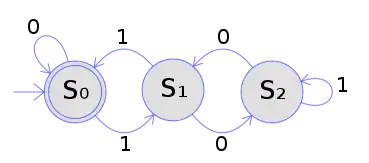
شکل سمت چپ، یک ماشین تعین‌پذیر حالات متناهی را با استفاده از نمودار حالت‌ها نشان می‌دهد. در این ماشین اتوماتا، سه حالت S₀، S₁ و S₂ وجود دارند (که در تصویر با دایره نشان داده شده‌اند). ماشین اتوماتا دنباله‌ای از ۰ها و ۱ها را به عنوان ورودی دریافت می‌کند. برای هر حالت، به ازای هر یک از ۰ و ۱، یک بردار انتقال موجود است که به حالت بعد راهنمایی می‌کند. تا زمانی که یک نماد را می‌خوانیم، یک DFA به صورت تعیین پذیر و قطعی با دنبال کردن بردارهای انتقال از حالتی به حالت دیگر حرکت می‌کند. برای مثال، اگر ماشین اتوماتا در حالت S₀ قرار دارد و نماد ورودی نیز ۱ است، به صورت قطعی به حالت S₁ خواهد رفت. یک DFA دارای یک حالت آغازین است (با فلشی که از هیچ کجا به آن وارد می‌شود، نشان داده می‌شود) که محاسبات در آن آغاز می‌شوند، و یک مجموعه از حالات نهایی (با دایره دوخطه نشان داده می‌شوند) که کمک می‌کند زمانی را که محاسبات موفق شده‌است را تعریف کنیم. یک DFA به عنوان یک مفهوم ریاضی مطلق تعریف شده‌است، اما با توجه به ذات نعیین‌پذیر DFA، قابل پیاده‌سازی در سخت‌افزار و نرم‌افزار برای حل مسائلی خاص و مختلف است. برای مثال یک DFA می‌تواند یک نرم‌افزار را که تصمیم می‌گیرد که آیا ورودی کاربر (برای مثال) یک آدرس ایمیل معتبر است یا نه، مدل کند. DFAها دقیقاً مجموعه زبان‌های منظم را که، به غیر از موارد دیگر، برای انجام آنالیزهای واژگانی و تطبیق‌های الگویی مفید هستند، می‌پذیرند. همچنین DFAها می‌توانند از طریق ساخت مجموعه توانی از ماشین‌های تعین‌ناپذیر حالات متناهی ساخته شوند.

تعریف رسمی

اتوماتون تعیین‌پذیر متناهی (Deterministic Finite Automaton - DFA) به یک پنج‌تائی ${\displaystyle M=(Q,\Sigma ,\delta ,q_{0},F)\!}$ گفته می‌شود، که شامل:

• ${\displaystyle Q\!}$ یک مجموعهٔ متناهی از حالات
• ${\displaystyle \Sigma \!}$ یک مجموعهٔ متناهی از نمادهای ورودی موسوم به الفبا
• ${\displaystyle q_{0}\!}$ حالت آغازین (q₀ ∈ Q)
• ${\displaystyle F\!}$ مجموعهٔ حالات نهائی یا مجموعهٔ حالات مورد قبول (F ⊆ Q)
• ${\displaystyle \delta \!}$ تابع انتقال (δ: Q × Σ → Q)

می‌باشد. فرض کنید w = a₁a₂ … a_n رشته‌ای از الفبای ${\displaystyle \Sigma \!}$ باشد. در این صورت رشته w توسط اتوماتون M پذیرفته می‌شود، اگر دنباله‌ای از حالات r₀,r₁, … , r_n در Q با شرایط زیر وجود داشته باشند:

1. r₀ = q₀
2. r_i+1 = δ(r_i, a_i+1), for i = 0, … , n−۱
3. r_n ∈ F.

به عبارت دیگر، شرط اول بیان می‌کند که ماشین با همان حالت آغازین q₀ شروع به محاسبه کند. شرط دوم بیان می‌کند که بر اساس هر یک از کاراکترهای رشته w داده شده، ماشین از حالتی به حالت دیگر طبق تابع انتقال δ انتقال خواهد یافت؛ و شرط آخر بیان می‌کند که ماشین w را می‌پذیرد، اگر آخرین ورودی w باعث توقف ماشین در یکی از حالات پایانی شود. در غیر این صورت، گفته می‌شود که اتوماتون رشته را رد کرده‌است. مجموعه همه رشته‌هایی که M می‌پذیرد، زبانیست که در M صدق می‌کند و این زبان با (L(M نشان داده می‌شود. ماشین تعین‌پذیر متناهی که حالت پایانی و آغازین ندارد به عنوان سیستم انتقال یا شبه‌اتوماتون شناخته می‌شود. برای آشنایی بیشتر با تعریف رسمی نظریه اتوماتا را ببینید.

مثال‌ها

مثال زیر، DFAی M با الفبای باینری است که ورودی‌هایی را که شامل تعداد زوجی ۰ هستند را می‌پذیرد.

نمودار حالات M

(M = (Q, Σ, δ, q₀, F که

• {Q = {S₁, S₂,
• {Σ = {۰, ۱,
• q₀ = S₁,
• {F = {S₁, و
• δ که با جدول انتقال حالت زیر تعریف می‌شود:

	0	1
S1	S2	S1
S2	S1	S2

حالت S₁ نشان‌دهنده این است که تاکنون تعداد زوجی ۰ در ورودی بوده است. در حالی که S₂ حاکی از تعداد فردی ۰ است. یک ۱ در ورودی حالت اتوماتون را تغییر نمی‌دهد. زمانی که ورودی پایان یابد، حالت اتوماتون نشان‌دهنده آن خواهد بود که آیا ورودی دارای تعداد زوجی ۰ است یا نه. اگر ورودی شامل تعداد زوجی ۰ باشد، M در حالت S₁ که حالتی پایانی است، پایان خواهد یافت و بنابراین رشته ورودی پذیرفته خواهد شد. زبانی که در M صدق می‌کند یک زبان منظم است که با عبارت منظم *((*۱)۰(*۱)۰)*۱ نشان داده می‌شود. "*" همان ستاره کلینی است؛ برای مثال *۱ نشان‌دهنده هر تعداد نامنفی (شاید صفر عدد) از نماد ۱ است.

ویژگی‌های بستاری

اگر زبانِ DFAی حاصل از اعمال عملیاتی بر DFAها قبل تشخیص با یک DFA باشد، گفته می‌شود که DFAها تحت آن عملیات بسته هستند. DFAها تحت عملیات زیر بسته هستند:

• اجتماع
• اشتراک
• الحاق
• ستاره کلین
• معکوس سازی
• Negation
• Init
• Quotient

ازآن‌جایی‌که DFAها هم‌ارز با ماشین‌های تعیین‌ناپذیر متناهی NFA هستند، ویژگی‌های بستاری بالا با استفاده از ویژگی‌های بستاری NFA‌ها اثبات می‌شوند.

شیوه‌های پذیرنده و تولیدکننده

یک DFA که نماینده یک زبان منظم است، می‌تواند هم به عنوان پذیرنده، برای تصدیق عضویت یک رشته ورودی در زبان، و هم به عنوان تولیدکننده، برای تولید لیستی از رشته‌های زبان، استفاده شود. در حالت پذیرنده، یک رشته ورودی فراهم شده است که اتوماتون می‌تواند آن را از چپ به راست، و هر بار یک نماد را بخواند. محاسبات از حالت آغازین شروع شده و با خواندن اولین نماد از رشته ورودی و دنبال کردن انتقال حالات طبق نمادها پیش می‌رود. سیستم به خواندن نمادها و دنبال کردن انتقال‌ها تا زمانی که دیگر هیچ نمادی در ورودی باقی نمانده باشد، که نشان‌دهنده پایان محاسبات است، ادامه می‌دهد. اگر پس از پایان یافتن پردازش همه نمادهای ورودی، سیستم در حالت پایانی باشد، خواهیم دانست که که رشته ورودی در واقع جزئی از زبان است، و گفته می‌شود که پذیرفته شده است؛ درغیراین‌صورت جزئی از زبان نبوده و پذیرفته نشده است. حالت تولیدکننده هم شبیه است؛ به غیر از این که علاوه‌بر تعیین اعتبار یک رشته ورودی، هدف آن تعین همه رشته‌های موجود در زبان است. به جای دنبال کردن یک انتقالِ خروجی از هر حالت، همه آن‌ها را دنبال می‌کند؛ و در عمل این با یک سری عملیات موازی سنگین (داشتن یک برنامه که هر بار با تصمیم‌گیری مواجه می‌شود به دو یا بیشتر پردازه انشعاب می‌یابد) یا از طریق محاسبات بازگشتی به انجام می‌رسد. مانند قبل، محاسبات از حالت آغازین شروع شده و سپس با دنبال کردن هر یک از انتقال‌های دردسترس پیش می‌رود، با آگاهی از این که کدام یک از شاخه‌ها انتخاب شده است. هر بار که اتوماتون خودش را در حالت پایانی بیابد، درمی‌یابد که دنباله‌ای از شاخه‌هایی که انتخاب شده است، یک رشته مورد قبول از زبان را تشکیل می‌دهد و آن رشته را به لیستی که در حال تولید آن است، اضافه می‌کند. اگر زبانی که این اتوماتون شرح می‌دهد، نامتناهی باشد (یعنی شامل تعداد نامتناهی از اعداد یا رشته‌ها باشد، مثلاً همه رشته‌های دودویی با تعداد زوجی صفر)؛ محاسبات هرگز متوقف نخواهد شد. مسلم است که زبان‌های منظم، به‌طورکلی، نامتناهی هستند، اتوماتا در حالت تولیدکننده گرایش بیشتر به ساخت نظری دارد.

DFA به عنوان انتقال مونوئید یا تکوار

بعلاوه، یک اجرا (run) می‌تواند به عنوان یک دنباله از ترکیب توابع انتقال با خودشان دیده شود. نماد ورودی ${\displaystyle a\in \Sigma }$ داده شده است، امکان دارد شخصی تابع انتقال را به صورت ${\displaystyle \delta _{a}:Q\rightarrow Q}$، با استفاده حیله ساده currying بنویسد که به صورت ${\displaystyle \delta (q,a)=\delta _{a}(q)}$ برای هر ${\displaystyle q\in Q}$ نوشته می‌شود. بدین صورت، تابع انتقال می‌تواند به صورت ساده‌تری دیده بشود: این تنها چیزیست که روی حالتی از Q «عمل می‌کند»، و به حالت دیگر می‌رود. ممکن است بدین صورت در نظر گرفته شود که نتیجه ترکیب توابعی است که مکرراً به توابع مختلف ${\displaystyle \delta _{a}}$, ${\displaystyle \delta _{b}}$ اعمال می‌شوند، و قس علی‌هذا. با استفاده از این مفهوم ${\displaystyle {\widehat {\delta }}:Q\times \Sigma ^{\star }\rightarrow Q}$ را تعریف می‌کنیم. دو حرف ${\displaystyle a,b\in \Sigma }$ داده شده است، ممکن است شخصی تابع جدید ${\displaystyle {\widehat {\delta }}}$ را با تکیه کردن بر ${\displaystyle {\widehat {\delta }}_{ab}=\delta _{a}\circ \delta _{b}}$ تعریف کند، که ${\displaystyle \circ }$ نشان‌دهنده ترکیب توابع است. به وضوح، این فرایند می‌تواند به صورت بازگشتی ادامه داده شود؛ بنابراین تعریف بازگشتی ذیل را داریم: ${\displaystyle {\widehat {\delta }}(q,\epsilon )=q.}$ که ${\displaystyle \epsilon }$ رشته تهی است و: ${\displaystyle {\widehat {\delta }}(q,wa)=\delta _{a}({\widehat {\delta }}(q,w)).}$ که ${\displaystyle w\in \Sigma ^{*},a\in \Sigma }$ و ${\displaystyle q\in Q}$. ${\displaystyle {\widehat {\delta }}}$ برای هر ${\displaystyle w\in \Sigma ^{*}}$ تعریف شده است. ترکیب مکرر توابع یک مونوئید یا تکوار را به وجود می‌آورد. برای تابع انتقال، این مونوئید به عنوان انتقال مونوئید یا گاهی شبه‌گروه تغییر شکل شناخته می‌شود. همچنین این ساخت می‌تواند برعکس شود: ${\displaystyle {\widehat {\delta }}}$ داده شده است، شخصی می‌تواند ${\displaystyle \delta }$ را دوباره‌سازی کند، و بنابراین هر دو توصیف معادلند.

منابع

• Sudkamp, T. A. , An Introduction to the Theory of Computer Science, Languages and Machines, 3rd ed. , Pearson Education, Inc. , 2006. ISBN 0-321-32221-5