درخت دودویی نخی
در یک درخت دودویی، تعداد اتصالات تهی، بیشتر از تعداد اتصالات غیرتهی است. در یک درخت دودویی از کل اتصالات یعنی 2n، تعداد n+1 اتصال تهی است. از این اتصالات تهی میتوان برای ارتباط با دیگر گرههای درخت استفاده کرد. در درختی که اتصالات تهی آن به این صورت استفاده شدهاست، درخت دودویی نخکشی شده (به انگلیسی: Threaded binary tree) نامیده میشود. یک درخت دودویی را میتوان به چند روش نخکشی کرد. این نخکشی بسته به روش پیمایش درخت دارد. برای مثال، درخت دودویی نخکشی شده به روش میانوندی به شکل زیر تعریف میشود:
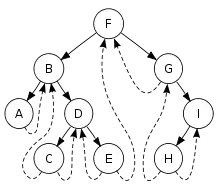
«برای هر گره، اتصال تهی سمت راست، به گره بعدی در پیمایش میانوندی اشاره کنند و اتصال تهی سمت چپ، به گره قبلی در پیمایش میانوندی اشاره کنند.»
درخت دودویی نخکشی شده این امکان را فراهم میسازد که پیمایش مقادیر در درخت دودویی به روش پیمایش خطی، سریعتر از پیمایش بازگشتی درخت به صورت میانوندی صورت گیرد. همچنین پیدا کردن والد یک گره در یک درخت دودویی نخی، بدون استفاده از اشارهگرهای والد یا بدون استفاده از پشته هم امکانپذیر است، هر چند که این کار کمی آهسته است. این قابلیت وقتی مفید است که فضای پشته اندک باشد یا وقتی که پشته اشارهگرهای والد غیرقابل دسترس باشد. (برای پیدا کردن گره والد به روش الگوریتم جستجوی عمق اول)
برای اینکه ببینیم این کار چگونه امکانپذیر است، گرهی به نام k را تصور کنید که یک فرزند سمت راست به نام r دارد. بنابراین اشارهگر سمت چپ r یا باید یک فرزند باشد یا یک اتصال نخی به k باشد. در مورد اول که r یک فرزند سمت چپ دارد، آن گره فرزند هم به نوبه خود یا باید یک فرزند سمت چپ داشته باشد یا باید اتصالی نخی به k باشد و به همین ترتیب این قضیه برای کلیه فرزندان سمت چپ صادق است. بنابراین با دنبال کردن زنجیرهای از اشارهگرهای سمت چپ گره r، ما بالاخره به گره k میرسیم. به شکل مشابه، اگر گرهی به نام p داشته باشیم که فرزند سمت چپ آن q است، با دنبال کردن زنجیره اشارهگرهای سمت راست q، بالاخره به p خواهیم رسید.
آرایه پیمایش میانوندی
نخها نشانهروهایی به گره ماقبل و گره مابعد گره فعلی هستند. گره ماقبل و گره مابعد بستگی به پیمایش یک درخت دارد که معمولاً از پیمایش میانوندی استفاده میشود. پیمایش میانوندی یک درخت دودویی به صورت ABCDEFGHI است. ماقبل گره E، گره D است و مابعد آن گره F است.
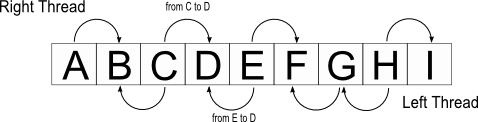
بنابراین کافیست اشارهگرهای تهی سمت راست هر گره را به گره مابعد آن و اشارهگر تهی سمت چپ هر گره را به گره ماقبل آن متصل کنیم. در شکل بالا اشارهگر تهی سمت راست E به F متصل شدهاست و اشارهگر تهی سمت چپ E به D متصل شدهاست.
مثال
درخت دودویی زیر را در نظر بگیرید:
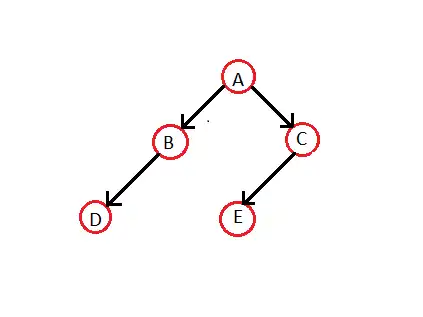
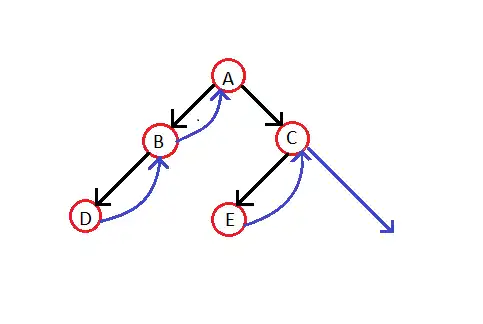
میخواهیم این درخت را بر اسا پیمایش میانوندی آن نخکشی کنیم. پیمایش میانوندی این درخت به صورت D B A E C است. حالا میتوان اشارهگرهای تهی سمت راست را به گره مابعد و اشارهگرهای تهی سمت چپ را به گره مابعد نخکشی کرد. شکل زیر پدید خواهد آمد:
الگوریتم
- گره جاری را بررسی کنید و ببینید آیا فرزند سمت چپی دارد که در لیست گرههای ملاقات شده وجود نداشته باشد؟ اگر داشت، به مرحله دو بروید، در غیر این صورت به مرحله ۳ بروید.
- فرزند چپ را به لیست گرههای ملاقات شده اضافه کنید و آن را گره فعلی خود در نظر بگیرید.
- گره جاری را بررسی کنید که آیا فرزند سمت راست دارد یا نه. اگر فرزند سمت راست داشت به مرحله ۴، در غیر این صورت به مرحله ۵ بروید.
- آن گره سمت راست را گره فعلی خود در نظر بگیرید و به مرحله ۶ بروید.
- اگر گره یک اتصال نخ داشت، آن را دنبال کنید. گرهی که از طریق نخ به آن رسیدهاید را گره جاری خود در نظر بگیرید.
- اگر گره دیگری وجود دارد به مرحله یک بروید، در غیر این صورت خارج شوید؛ درخت پیمایش شدهاست.
حال درخت زیر را در نظر بگیرید:

| Li | ||||
|---|---|---|---|---|
| مرحله اول | 'A' گره سمت چپی به نام B دارد که هنوز ملاقات نشدهاست، بنابرایت ما B را به «لیست گرههای ملاقات شده اضافه میکنیم و سپس B را گره جاری خود در نظر میگیریم. | B | ||
| مرحله ۲ | 'B هم یک فرزند چپ به نام D دارد که هنوز ملاقات نشدهاست. بنابراین D را به لیست خود اضافه کرده و آن را گره جاری خود فرض میکنیم. | B D | ||
| مرحله ۳ | 'D فرزند چپ ندارد، بنابراین ما D را چاپ میکنیم. سپس فرزند راست آن را بررسی میکنیم. D فرزند راست ندارد و بنابراین ما پیوند نخ آن را بررسی میکنیم. اتصال نخ به گره B رفته است. بنابراین ما B را گره جاری خود فرض میکنیم. | B D | D | |
| مرحله ۴ | 'B یقیناً یک فرزند چپ دارد، اما ما قبلاً آن را به لیست گرههای ملاقات شده اضافه کردهایم. بنابراین ما B را چاپ میکنیم. سپس فرزند راست آن را بررسی میکنیم، اما فرزند راست وجود ندارد. بنابراین ما اتصال نخ آن را دنبال میکنیم و به گره A میرسیم و سپس A را گره جاری خود فرض میکنیم. | B D | D B | |
| مرحله ۵ | 'A یک فرزند چپ دارد که قبلاً ملاقات شدهاست. پس ما A را چاپ میکنیم. سپس ما فرزند راست آن را بررسی میکنیم که C است و هنوز در لیست گرههای ملاقات شده وجود ندارد. بنابراین ما آن را به لیست اضافه کرده و سپس آن را گره جاری قرار میدهیم. | B D C | D B A | |
| مرحله ۶ | 'C یک گره چپ به نام E دارد که هنوز ملاقات نشده و در لیست وجود ندارد. بنابراین ما آن را به لیست اضافه میکنیم و سپس آن را گره جاری خود فرض میکنیم. | B D C E | D B A | |
| مرحله ۷ | به همین ترتیب... | D B A E C | ||
منابع
مشارکتکنندگان ویکیپدیا. «Threaded binary tree». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۹ اوت ۲۰۱۳.