دستور زبان مبهم

در علوم رایانه یک دستور زبان مبهم گرامر مستقل از متن است که در آن رشته ای وجود دارد که می‌تواند بیش از یک اشتقاق ازسمت چپ داشته باشد. در حالیکه یک دستور زبان غیر مبهم, یک دستورزبان مستقل از متن است که هر رشتهٔ معتبری در آن زبان تنها یک اشتقاق چپ داشته باشد. برای بیشتر زبانها می‌توان دو دستور زبان مبهم و غیر مبهم نوشت. اما برای بعضی زبانها تنها دستور زبان مبهم می‌توان نوشت. برای هر زبان غیر تهی می‌توان یک دستوز ربان مبهم به وسیله در نظر گرفتن دستور زبان بدون ابهام و معرفی قاعده‌های تکرار یا مترادف نوشت. (زبان تهی تنها زبانی است که دستوز ربان مبهم ندارد) به زبانی که تنها دستورزبان مبهم دارد زبان ذاتاً مبهم گویند و زبان مستقل از متن ذاتاً مبهم وجود دارد. گرامرهای مستقل از متن قطعی همیشه غیر مبهم اند؛ و یک زیرگروه مهمی از CFGهای بدون ابهام هستند. با این حال CFGهای بدون ابهام غیر قطعی نیز وجود دارد.

مثال

ساده‌ترین مثال دستور زبان مبهم زیر برای زبان بی‌اهمیت است، که تنها متشکل از رشته خالی است:

A → ε

B → ε

…به این معنی که رشتهٔ تهی ϵ را می‌توان با هرکدام از دو معادلهٔ تولید بالا به دست آورد و در نتیجه دارای دو اشتقاق چپ است. دستور زبان دیگر برای زبان بی‌اهمیت به شکل زیر موجود است:

A → A | ε

…به این معنی که تولید می‌تواند خود رشته یا رشتهٔ تهی باشد؛ بنابراین رشته خالی مشتقات سمت چپ به طول ۱، ۲، ۳ و در واقع از هر طولی است، بسته به اینکه چند بار قاعدهٔ A → استفاده شده‌است. این زبان دارای دستورزبان غیر مبهم است که تنها شامل یک قاعدهٔ تولید :A → ε است. …به این معنی که تولید یکتا می‌تواند تنها یک رشتهٔ خالی تولید کند که تنها رشتهٔ موجود در زبان است. به عبارت دیگر به وسیلهٔ اضافه کردن موارد تکراری می‌توان برای زبان‌های غیر تهی دستورزبان مبهم ساخت.

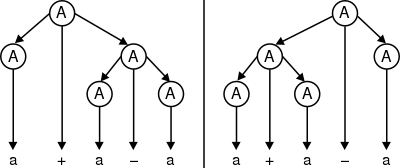
جمع و تفریق

گرامر مستقل از متن

A → A + A | A − A | a

چون دو تا اشتقاق چپ برای رشتهٔ a + a + a وجود دارد.

	A	→ A + A		A	→ A + A
		→ a + A			→ A + A + A
		→ a + A + A			→ a + A + A
		→ a + a + A			→ a + a + A
		→ a + a + a			→ a + a + a

گرامر مثال بعدی نیز مبهم است چون دو نمودار درختی برای رشتهٔ a + a − a وجود دارد.

زبانی که تولید می‌کند ذاتاً مبهم نیست. دستورزبان زیر دستورزبانی غیرمبهم برای آن است.

A → A + A | A − a | a

شناخت دستور زبان‌های مبهم

به‌طور کلی نمی‌توانیم مستقیم بگوییم دستورزبانی مبهم است. راندمان تجزیهٔ دستور زبان مستقل از متن به وسیلهٔ ماشینی که آن را می‌پذیرد مشخص می‌شود. گرامرهای مستقل از متن قطعی به وسیلهٔ ماشین قطعی پشته‌ای پذیرفته می‌شوند؛ و می‌توانند در زمان خطی تجزیه شوند. به عنوان مثال می‌توان تجزیه کنندهٔ LR این یک زیرمجموعه‌ای از گرامر مستقل از متن است که به وسیلهٔ ماشین پشته‌ای پذیرفته شده و می‌تواند در زمان چند جمله‌ای تجزیه شود. به عنوان مثال می‌توان الگوریتم سی وای کا را نام برد. دستورزبان مستقل از متن غیر مبهم می‌تواند غیر قطعی باشد به عنوان مثال زبان واروخوانه با طول زوج که روی الفبای ۰ و ۱تعریف شده‌است دستورزبان مستقل از متن نامبهمS → 0S0 | 1S1 | ε را دارد نام برد. . یک رشتهٔ دلخواه از این زبان بدون خواندن همهٔ حروف اول نمی‌تواند تجزیه شود. با این وجود نتیجهٔ از بین بردن ابهام دستور زبان ممکن است دستورزبان مستقل از متن باشد و همین باعث بالارفتن راندمان تجزیه اش شود. تولیدکننده‌های کامپایلر مانند [یک (کامپایلر)](YACC) شامل امکاناتی برای رفع بعضی از انواع ابهام هستند.

زبان‌های ذاتاً مبهم

ذاتاً مبهم توسط قضیهٔ پاریخ Parikh's theore در سال ۱۹۶۱ توسط Rohit Parikh در یک گزارش تحقیقاتی MIT اثبات شده‌است. با وجود اینکه بعضی از زبان‌های مستقل از متن (مجموعه‌ای از رشته‌ها که می‌توانند توسط دستورزبان تولید شوند) دو دستورزبان مبهم و غیر مبهم دارند. زبان مستقل از متنی وجود دارد که هیچ دستورزبان غیرمبهم مستقل از متنی نمی‌تواند داشته باشد. به عنوان مثال از این زبان می‌توان مجموع${\displaystyle \{a^{n}b^{n}c^{m}d^{m}|n,m>0\}}$ و ${\displaystyle \{a^{n}b^{m}c^{m}d^{n}|n,m>0\}}$را نام برد. این مجموعه از آن جهت مستقل از متن است که از اجتماع دو زبان مستقل از متن تشکیل شده‌است. اما (Hopcroft & Ullman (1979 ثابت کردند که راهی وجود ندارد که بتوان رشته‌های درون زیر مجموعهٔ ${\displaystyle \{a^{n}b^{n}c^{n}d^{n}|n>0\}}$ که اشتراک دو زبان است را غیر مبهم تجزیه کرد.

منابع

• Wikipedia contributors, "Ambiguous grammar," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Ambiguous_grammar&oldid=637748029 (accessed January 21, 2015).