رمز ویژنر

سایفر ویژنر روشی برای رمزنگاری یک متن الفبایی با استفاده از روش سزار بر مبنای حروف یک کلمهٔ کلید می‌باشد. در واقع شکل دیگری از روش رمزنگاری جانشینی[1] است.

Blaise de Vigenère

اولین بار در سال ۱۵۵۳ توسط Giovan Battista Bellaso[2] بیان شد. علاوه بر این که رمزنگاری ساده فهمی بود و به راحتی پیاده‌سازی می شد، در برابر تمام تلاش‌ها برای شکستن مقاومت نیز کرد تا این که بعد از سه قرن در سال ۱۸۶۳ شکسته شد. به همین دلیل به این نوع رمزنگاری، لقب le chiffre indéchiffrable (یعنی رمز غیرقابل رمزگشایی) را دادند. خیلی از افراد سعی کردند تا طرحهایی از رمزنگاری را پیاده‌سازی کنند که در واقع همهٔ آن‌ها براساس رمزنگاری ویژنر بود. در سال ۱۸۶۳ Friedrich Kasisk[3]i روشی برای رمزگشایی متون رمز شده با شیوهٔ ویژنر ارائه داد.

در قرن نوزدهم این طرح به اشتباه به Blaise de Vigenère[4] نسبت داده شد به همین دلیل نام این رمزنگاری ویژنر است.

تاریخچه

لئون باتیستا آلبرتی اولین کسی بود که تعریف جامعی از رمز چند الفبایی ارائه داد. او از یک دیسک رمزنگاری آهنین برای جانشینی بین حروف رمز استفاده می‌کرد. سیستم آلبرتی تنها بعد از چند کلمه حروف را تغییر می‌داد. منظور از سوییچ، نوشتن حرف متناسب با حرف الفبایی رمز شده در متن رمز شده بود. بعدها یوهانس تریتمیوس در یک تحقیق مربوط به رمزنگاری ، tabula recta[5] را منتشر کرد و این جدول در واقع جدولی مربعی از حروف الفبا است که شیفت داده شده‌اند و از ابزار مهم در رمزنگاری ویژنر است. روش رمزنگاری تریتمیوس ، پیشرفت چشم‌گیری به جای سوییچ‌های بین حروف حروف متن رمز شده که سخت‌افزاری و قابل پیش‌بینی بودند، ارائه می‌داد.

جدول ویجنر

در سال ۱۵۸۶، Blaise de Vigenère یک نوع رمزنگاری چند الفبایی(polyalphabetic) به نام رمزنگاری autokey را منتشر کرد زیرا کلید آن بر اساس متن اصلی استوار است. رمزنگاری که اکنون به عنوان رمز Vigenère شناخته می‌شود، در ابتدا توسط Giovan Battista Bellaso در کتاب ۱۵۵۳ خود La cifra del Sig شرح داده شده‌است. رمزنگاری او براساس tabula recta است با این تفاوت که از یک کلید (countersign) استفاده می‌کند که برای هر حرف، حروف رمزنگاری تغییر کنند. در حالی که آلبرتی و تریتمیوس از الگوی ثابت جایگزینی استفاده می‌کردند، طرح Bellaso به این معنی بود که الگوی substitutions را می‌توان به سادگی با انتخاب یک کلید جدید تغییر داد. کلیدها معمولاً کلمه‌های منفرد یا عبارت‌های کوتاه بودند؛ بنابراین در روش Bellaso امنیت قوی تنها به کلید آن بستگی داشت. از آنجا که تهیه یک عبارت کلیدی کوتاه، مانند مکالمه خصوصی قبلی، نسبتاً آسان است، سیستم Bellaso از امنیت قابل توجهی برخوردار بود. در قرن نوزدهم، اختراع رمزگذاری Bellaso به نادرستی به Vigenère نسبت داده شد. David Kahn, در کتاب خود، "Codebreakers" با ابراز تاسف از این سوء تفسیر، اظهار داشت که تاریخ "این سهم مهم را نادیده گرفته‌است و در عوض یک رمزنگاری ابتدایی را برای وی [Vigenère] نامگذاری کرده‌است، گرچه هیچ ارتباطی با آن نداشت". رمزنگاری Vigenère به دلیل قوی بودن و امنیتش شهرت پیدا کرد. چارلز لوتویج داگسون (نویسنده و ریاضیدان مشهور)، رمزنگاری Vigenère را در اثر خود در سال 1868 "The Alphabet Cipher" در یک مجله کودک غیرقابل شکست می‌نامد. در سال ۱۹۱۷، دانشمندی آمریکایی رمزنگاری Vigenère را "ترجمهٔ نشدنی (impossible of translation)" توصیف کرد. چارلز بابیج شناخته شده‌است در این که متون رمز شدهٔ متنوعی را در اوایل سال ۱۸۵۴ شکست اما هیچ‌گاه کار خود را منتشر نکرد. Kasiskبه‌طور کامل رمزنگاری را شکست و در قرن نوزدهم این تکنیک را منتشر کرد، اما حتی در قرن شانزدهم، بعضی از رمزنگاران ماهر می‌توانستند گاه به گاه رمز را بشکنند. رمزگذاری Vigenère به اندازهٔ کافی ساده هستند که در صورت استفاده از دیسک‌های رمزگذاری، رمزگذاری می‌شود. به عنوان مثال، کشورهای کنفدراسیون آمریکا از دیسک رمزنگاری برای پیاده‌سازی رمز Vigenère در طول جنگ داخلی آمریکا استفاده کردند. پیام‌های کنفدراسیون پنهان نمی‌ماندند و اتحادیه مرتباً پیام‌های آن‌ها را کرک می‌کرد. در طول جنگ، رهبری کنفدراسیون در درجه اول به سه عبارت اساسی به عنوان کلید تکیه می‌کرد: "Manchester Bluff" , "Complete Victory" و وقتی که جنگ به پایان رسید، "Come Retribution". رمزنگاری Vernam که کلید آن تا زمانی که پیام به one-time pad[6] تبدیل نشود، از نظر تئوری، یک رمزنگاری ناگسستنی است. Gilbert Vernam سعی کرد رمز شکسته (ایجاد رمز Vernam-Vigenère در سال ۱۹۱۸) را ترمیم کند، اما فناوری که او از آن استفاده کرده بود آنقدر دست و پاگیر و پیچیده بود که عملاً نشدنی بود.

توصیف

---

در رمزنگاری Caesar،[7] هر حرف از الفبایی به اندازهٔ عدد مشخصی شیفت پیدا می‌کند. به عنوان مثال، در رمزنگاری Caesar شیفت به اندازهٔ ۳ واحد به این صورت است که، A می‌شود D , B می‌شود E , Y می‌شود B و غیره. رمزگذاری Vigenère دارای چندین رمز Caesar به همراه مقادیرمتفاوتی برای شیفت دادن، است. (different shift values)

برای رمزگذاری، می‌توان از جدول حروف استفاده کرد که به آن یک tabula recta، مربع Vigenère یا جدول Vigenère گفته می‌شود. این حروف الفبا ۲۶ بار در ردیف‌های مختلف نوشته شده‌است، هر الفبا در مقایسه با الفبای قبلی، شیفت چرخه ای به چپ دارد، متناسب با ۲۶ حالت رمزگذاری Caesar است. در نقاط مختلف فرایند رمزگذاری، از حرف الفبایی متفاوتی از یکی از ردیف‌ها استفاده می‌شود. الفبای مورد استفاده در هر نقطه به آن کلید (repeating keyword) بستگی دارد.

به عنوان مثال متنی زیر را که می‌خواهیم رمزنگاری کنیم، در نظر بگیرید:

$${\displaystyle ATTACKATDAWN}$$

شخصی که پیام را ارسال می‌کند یک کلمه را به عنوان کلید انتخاب می‌کند و آن را تکرار می‌کند تا اینکه با طول متن اصلی برابر شود. به عنوان مثال، کلمه کلیدی "LEMON" را بعنوان کلید استفاده می‌کند:

$${\displaystyle LEMONLEMONLE}$$

هر ردیف با یک حرف کلیدی شروع می‌شود. اگرچه ۲۶ ردیف کلیدی نشان داده شده‌است، یک کد فقط از همان کلیدهایی (حروف مختلف) استفاده می‌کند که در رشتهٔ کلید آمده‌است. در این مثال فقط ۵ کلید خواهیم داشت: L, E، M, O، N.

حروف پشت سر هم از متن اصلی همراه با حروف کلید در نظر گرفته می‌شود. حال با در نظرگیری یک حرف از متن اصلی و حرف متناظر در کلید، در جدول عنصر [key-row, msg-col] را پیدا می‌کنیم و آن را به عنوان حرف رمز شده درنظر می‌گیریم.

به عنوان مثال، اولین حرف متن اصلی، A ، با L، حرف اول از کلید متناظر هم می‌شوند؛ بنابراین، از ردیف L و ستون A از جدول Vigenère استفاده می‌شود، یعنی L. به همین ترتیب، برای حرف دوم متن ساده از حرف دوم کلید استفاده می‌شود. حرف ردیف E و ستون X ,T است. بقیه متن به روشی مشابه رمزگذاری می‌شوند.

Plaintext (متن اصلی):	ATTACKATDAWN
Key (کلید):	LEMONLEMONLE
Ciphertext (متن رمز شده):	LXFOPVEFRNHR

رمزگشایی با مراجعه به ردیف مربوط به کلید، پیدا کردن جایگاه حرف رمزشده در آن سطر و سپس استفاده از برچسب ستون به عنوان حرف متن ساده انجام می‌شود. به عنوان مثال، در ردیف L (از LEMON) متن رمزنگاری L در ستون A ظاهر می‌شود که اولین حرف ساده است. در مرحله بعد، در ردیف E (از LEMON)، متن رمزگذاری شده X در ستون T قرار دارد؛ بنابراین T حرف دوم حرف ساده است.

توصیف جبری

---

Vigenère را نیز می‌توان از نظر جبری تعریف نمود. اگر به حروف A-Z اعداد ۲۵–۰ نسبت داده شود ${\displaystyle (A\equiv 1,B\equiv 1)}$ و جمع را بر مبنای ۲۶ در نظر بگیریم، رمزنگاری (Vigenère (E را با کلید (K) می‌توان به شکل زیر نوشت:

$${\displaystyle C_{i}=E_{K}(M_{i})=(M_{i}+K_{i})mod26}$$

همچنین رمزگشایی (D) با استفاده از کلید (K) را می‌توان به صورت زیر تعریف کرد:

$${\displaystyle M_{i}=D_{K}(C_{i})=(C_{i}-K_{i}+26)mod26}$$

که در دو تعریف بالا M = M₁ …M_n متن اصلی است، C = C₁ …C_n متن رمز شده‌است و K = K₁ …K_n کلیدی است که از نتیجهٔ تکرار کلمهٔ کلیدی به تعداد [n/m] به دست آمده‌است که m طول کلید می‌باشد. پس با استفاده از مثال قبل، برای رمزنگاری کردن ${\displaystyle A\equiv 1}$ با حرف کلیدی ${\displaystyle L\equiv 11}$ ، نتیجه خواهد شد:

$${\displaystyle 11=(0+11)mod26}$$

بنابراین برای رمزگشایی ${\displaystyle R\equiv 17}$ با استفاده از حرف کلیدی ${\displaystyle E\equiv 4}$ ، به شکل زیر عمل می‌کنیم:

$${\displaystyle 13=(17-4)mod26}$$

به‌طور کلی اگر ∑ مجموعه ای از حروف الفبایی با طول ${\displaystyle l}$ باشد و m طول کلید باشد، می‌توان رمزنگاری و رمزگشایی Vigenère به شکل زیر نشان داد:

$${\displaystyle C_{i}=E_{K}(M_{i})=(M_{i}+K_{(}i\,mod\,m))mod\,\,l}$$

M_i متناسب است با مقداری که برای i امین کاراکتری که در جدول در نظر گرفته شده‌است به عنوان مثال اگر مجموعهٔ حروف الفبایی به صورت باشد ${\displaystyle \Sigma =\{A,B,C,...,X,Y,Z\}}$ مقدار A برابر با صفر خواهد بود همچنین مقدار B برابر با یک خواهد بود و … به همین صورت برای C_i و K_i.

تحلیل رمز (cryptanalysis)

---

ایده ای که در رمزنگاری Vigenère مانند سایر رمزنگاری‌های چندالفبایی (polyalphabetic) کاربرد دارد این است که تعداد تکرار هر حرف را به صورت مستقیم در تحلیل آماری فرکانس استفاده می‌کند. به عنوان مثال، اگر P پر تکرارترین حرف در متن باشد، با توجه به این که آن متن به زبان انگلیسی است، ممکن است گمان شود که P با E مطابقت دارد، زیرا E پرتکرارترین حرف در زبان انگلیسی است؛ بنابراین در رمزنگاری Vigenère، حرف E در هر نقطه ای از متن اصلی می‌تواند به هر حرف دیگری رمزنگاری شود که تحلیل فرکانسی می‌تواند این سیستم را بشکند.

بزرگترین ضعف رمزنگاری Vigenère، تکرار کلید آن است. اگر بتوان طول کلید را حدس زد، با متن رمزنگاری شده می‌توان مشابه رمزنگاری Caesar[8] رفتار کرد و با استفاده از تحلیل فرکانسی حروف، سیستم رمزنگاری را شکست. با استفاده از روش Kasiski و تست Friedman، می‌توان طول کلید را تعیین کرد.

آزمون Kasiski

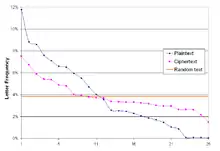
در سال ۱۸۶۳، Friedrich Kasiski اولین کسی بود که یک حمله موفقیت‌آمیز به رمزنگاری Vigenère را منتشر کرد. حمله‌های قبل از آن در صورت داشتن دانشی از متن اصلی یا با استفاده از کلید قابل حدسی صورت می‌گرفت در حالی که روش Kasiski به این دو وابسته نبود. اگرچه Kasiski نخستین کسی بود که شرحی از این حمله را منتشر کرد، اما واضح است که دیگران از آن آگاه بودند. در سال ۱۸۵۴، هنگامی که John Hall Brock Thwaites رمزهای جدید را به ژورنال انجمن هنرها ارسال کرد، Charles Babbage[9] در تلاش برای شکستن رمز Vigenère بود. وقتی Babbage نشان داد که رمزنگاری Thwaites در واقع بازآفرینی دیگری از رمزگذاری Vigenère است، Thwaites چالشی را برای Babbage مطرح کرد: با توجه به متن اصلی (دیالوگی از نمایش The Tempest برگرفته از شکسپیر) و نسخه رمزگذاری شده آن، وی بایست کلیدی که Thwaites برای رمزنگاری متن اصلی استفاده کرده بود، پیدا می‌کرد. Babbage سریعاً کلمه‌های کلیدی را پیدا کرد: "two" و "combined". پس از آن Babbage با استفاده از کلمه‌های کلیدی مختلف، متنی مشابه از شکسپیر را رمزگذاری کرد سپس Thwaites را برای یافتن کلمه‌های کلیدی به چالش کشید. Babbage هرگز روشی را که استفاده کرد توضیح نداد. یادداشت‌های Babbage نشان می‌دهد که وی از روشی که بعدها توسط Kasiski منتشر شده استفاده کرده‌است و نشان می‌دهد که وی از اوایل سال ۱۸۴۶ از این روش استفاده می‌کرد. تست Kasiski از این واقعیت استفاده می‌کند که کلمه‌های پرتکرار، به‌طور اتفاقی، گاهی با استفاده از حروف کلیدی مشابه رمزگذاری شده‌اند و منجر به گروه‌های پرتکرار در متن رمز شده، می‌شوند. به عنوان مثال، رمزگذاری زیر را با استفاده از کلید واژه ABCD در نظر بگیرید:

key: ABCDABCDABCDABCDABCDABCDABCD

Plaintext: CRYPTOISSHORTFORCRYPTOGRAPHY

Ciphertext: CSASTPKVSIQUTGQUCSASTPIUAQJB

تکرار به راحتی در متن رمزنگاری شده مشاهده می‌شود، بنابراین تست Kasiski مؤثر خواهد بود. فاصله بین تکرارهای CSAST، ۱۶ است. اگر فرض شود که بخش‌های تکرار شده در متن رمز شده، همان بخش‌های تکراری در متن اصلی را نشان می‌دهد، این بدان معنی است که طول کلید ۱۶، ۸ ، ۴، ۲ یا ۱ کاراکتر است. تمام مقسوم علیه‌های فاصله، می‌توانند به عنوان کاندید برای طول کلید باشند به عنوان مثال کلید به طول یک همان رمز نگاری Caesar است و تحلیل رمز آن بسیار ساده‌تر است. از آنجا که طول کلید ۲ و ۱ غیر واقعی و کوتاه هستند، پس کافی است طول‌های ۱۶، ۸ یا ۴ را امتحان کرد. پیام‌های طولانی‌تر عملکرد این تست را دقیق تر می‌کند زیرا معمولاً حاوی بخش‌های تکراری بیشتری است. متن رمز شدهٔ زیر شامل دو بخش است که تکرار می‌شود:

Ciphertext: VHVSSPQUCEMRVBVBBBVHVSURQGIBDUGRNICJQUCERVUAXSSR

فاصله بین تکرارهای VHVS، ۱۸ است. اگر فرض شود که بخش‌های تکرار شده در متن رمز شده، همان بخش‌های تکراری در متن اصلی را نشان می‌دهد، این بدان معنی است که طول کلید ۱۸، ۹ ، ۶، ۳ ، ۲ یا ۱ کاراکتر است. فاصله بین تکرارهای QUCE، ۳۰ کاراکتر است. این بدان معنی است که طول کلید می‌تواند ۳۰، ۱۵، ۱۰، ۶ ، ۵، ۳ ، ۲ یا ۱ کاراکتر باشد. با اشتراک گرفتن بین این دو مجموعه، با اطمینان می‌توان نتیجه گرفت که به احتمال زیاد طول کلید ۶ است زیرا طول‌های ۳، ۲ و ۱ غیر واقعی و کوتاه هستند.

تست Friedman

آزمایش Friedman (با نام تست کاپا نیز شناخته می‌شود) در دهه ۱۹۲۰ توسط William F. Friedman[10] اختراع شد که از شاخص تصادف (index of coincidence) استفاده کرد که ناهماهنگی بین فرکانس‌های تکرار حروف رمزنگاری شده برای شکستن سیستم اندازه‌گیری می‌کند. با دانستن احتمال ${\displaystyle k_{p}}$ که احتمال یکسان بودن دو حرف از یک متن که تصادفی انتخاب می‌شوند را بیان می‌کند (حدوداً ۰٫۰۶۷ در زبان انگلیسی) و احتمال انتخاب تصادفی uniform یک حرف از حروف الفبا (در زبان انگلیسی (${\displaystyle 1/26}$) یا ${\displaystyle k_{r}=0.0385}$)، طول کلید با رابطهٔ زیر تخمین زده می‌شود:

$${\displaystyle (k_{p}-k_{r})/(k_{o}-k_{r})}$$

${\displaystyle k_{o}}$ نرخ همزمانی مشاهده شده را نشان می‌دهد:

$${\displaystyle k_{o}=\sum _{i=1}^{c}(n_{i}(n_{i}-1))/N(N-1)}$$

در فرمول بالا:

c تعداد حرف در الفبا است (در زبان انگلیسی ۲۶ = c).

${\displaystyle N}$ طول متن را نشان می‌دهد.

${\displaystyle n_{1}}$ تا ${\displaystyle n_{c}}$، فرکانس تکرار حرف مشاهده شده در متن رمز شده‌است.

با این حال، فرمول بالا تنها یک تقریب است؛ دقت آن با افزایش اندازه متن افزایش می‌یابد. در عمل، لازم است طول‌های کلیدی مختلف را که نزدیک به تخمین هستند، امتحان شود. یک روش بهتر برای بررسی طول‌های مختف کلید، کپی کردن متن در سطرهای یک ماتریس با تعداد ستون‌های مختلف به اندازهٔ طول کلیدی فرضی و سپس میانگین شاخص همزمانی (IC) ستون‌ها که محاسبه می‌شود. وقتی این کار برای هر طول کلید ممکن انجام شود، طول کلید متناظر با بالاترین میانگین I.C. به احتمال زیاد همان طول کلید به کاربرده شده‌است. چنین آزمایش‌هایی ممکن است توسط دانش مربوط به آزمون Kasiski تکمیل شود.

تحلیل فرکانس (Frequency analysis)

هنگامی که طول کلید تعیین شد، متن رمزشده را می‌توان در ستون‌ها بازنویسی کرد، که هر ستون مربوط به یک حرف اصلی از کلید است. هر ستون شامل متن ساده است درواقع مثل این است که از رمزنگاری Caesar استفاده شده‌است. کلید Caesar (shift)، یک حرف از کلید Vigenère است که برای آن ستون استفاده شده‌است. با استفاده از روشهای مشابه برای شکستن رمز Caesar، می‌توان حروف موجود در متن رمز شده را کشف کرد. روش جامع تری از آزمون Kasiski، معروف به روش Kerckhoffs، فرکانس‌های حرف هر ستون را با فرکانس‌های متن ساده اصلی که شیفت پیدا کرده، مطابقت می‌دهد تا حرف اصلی (Caesar shift) را برای آن ستون کشف شود. هنگامی که هر حرف در کلید مشخص شد، آنچه باید توسط تمام تحلیلگران رمز انجام شود این است که متن رمز شده را رمزگشایی می‌کنند تا متن اصلی را به دست آورند. در صورتی که جدول Vigenère از ترتیب حروف الفبایی نرمال بهره نگیرد، روش Kerckhoffs کاربردی ندارد، اما آزمایش Kasiski و تست‌های تصادفی (coincidence) هنوز هم می‌توانند برای تعیین طول کلید استفاده شوند.

از بین بردن کلید (Key elimination)

در رمزنگاری Vigenère که با الفبای نرمال و رایجی همراه است، در اصل از حساب پیمانه ای یا همنهشتی استفاده می‌کند که خاصیت جابه جایی دارد به خاطر همین با تفاضل متن رمز شده با خودش به این صورت که متن رمز شده را با تبدیل به بلاک‌هایی به اندازهٔ طول کلید می‌کنند و بلاک‌های پشت سر هم را از هم کم می‌کنند، که حاصل برابر است با تفاضل متن اصلی با خودش به همان صورتی که برای متن رمز شده گفته شد. حال اگر بتوان در آن یک کلمهٔ احتمالی را پیدا کرد یا حدس زد پس خودرمزنگاری که بر روی متن اصلی اعمال شده شناخته می‌شود. همین فرایند باعث می‌شود که بتوان کلید را با استفاده از تفاضل متن اصلی شناخته شده و متن رمز شده، پیدا کرد. روش Key elimination برای پیام‌هایی با طول کم کاربرد دارد.

انواع دیگر

---

نوعی کلیدی اجرایی از رمزگذاری Vigenère نیز در شرایطی غیرقابل شکست تلقی می‌شد. این نسخه وقتی طول کلید به اندازهٔ طول متن اصلی باشد، کاربرد دارد. از آنجا که کلید به اندازهٔ پیام است، تست Friedman و Kasiski دیگر کار نمی‌کنند، زیرا این کلید فرایند تکرار را دیگر ندارد. در صورت استفاده از چندین کلید، طول کلید مؤثر برابر است با کوچکترین مضرب مشترک بین کلیدها. به عنوان مثال، با استفاده از دو کلید GO و CAT که طول آنها ۲ و ۳ است، طول کلید مؤثر ۶ (ک.م. م ۲ و ۳) خواهد بود. همین باعث می‌شود که دو کلید با طول یکسانی به صف شوند. به‌طور مثال:

Plaintext:	ATTACKATDAWN
Key 1:	GOGOGOGOGOGO
Key 2:	CATCATCATCAT
Ciphertext:	IHSQIRIHCQCU

رمزگذاری دو بار صورت می‌گیرد، ابتدا با کلید GO و سپس با کلید CAT و معادل یک بار رمزگذاری با کلیدی است که از رمزنگاری یکی از این دو کلید با کلید دیگر به دست می‌آید. مطابق عبارت زیر:

Plaintext:	GOGOGO
Key:	CATCAT
Ciphertext:	IOZQGH

با رمزگذاری ATTACKATDAWN با IOZQGH آنچه در بالا ذکر شد، اثبات می‌شود، برای تولید همان متن رمز شده مشابه در مثال گفته شده:

Plaintext:	ATTACKATDAWN
Key:	IOZQGHIOZQGH
Ciphertext:	IHSQIRIHCQCU

اگر طول هر کدام از کلیدها عدد اول باشد، طول کلید مؤثر به صورت نمایی با افزایش طول کلیدها، افزایش می‌یابد. این عبارت زمانی برقرار است که طول هر کدام از کلیدها عددی اول باشد. به عنوان مثال، طول کلید مؤثر با کلیدهایی به طول ۲، ۳ و ۵ کاراکتر، ۳۰ است، اما با کلیدهای به طول ۷، ۱۱ و ۱۳ کاراکتر، ۱۰۰۱ است. اگر این طول کلید مؤثر طولانی‌تر از متن رمز شده باشد، در برابر آزمون‌های Friedman و Kasiski همانند آنچه دربارهٔ رمزهای اجرایی چندی قبل گفته شد، ایمن است.

اگر واقعاً از یک کلید تصادفی تولید شود، طول آن حداقل به اندازهٔ متن رمز شده باشد و فقط یک بار از آن استفاده شود، رمزنگاری Vigenère از نظر تئوری غیرقابل شکست خواهد بود. با این وجود، در این حالت کلید، و نه رمزگذاری، رمزنگاری را از نظر شکست پذیری، قدرت می‌بخشد، و این سیستم‌ها صرف نظر از شیوهٔ رمزنگاری به کار رفته، به عنوان سیستم‌های (one-time pad) خوانده می‌شوند. Vigenère در واقع یک شیوهٔ رمزنگاری قوی تر، autokey[11] را اختراع کرد؛ ولی نام رمزنگاری Vigenère به یک رمزنگاری چند الفبایی (polyalphabetic) ساده‌تر نسبت داده شده‌است. اما در حقیقت دو روش رمزنگاری با یکدیگر ترکیب شده‌اند و اغب به آن le chiffre indéchiffrable می‌گویند. Babbage در حقیقت رمزنگاری بسیار قوی autokey را شکست داد، اما معمولاً Kasiski به عنوان اولین راه حل منتشر شده برای رمزنگاری چندالفبایی (polyalphabetic) با کلید ثابت کاربرد دارد. یک نوع ساده از رمزنگاری استفاده از شیوهٔ رمزگشایی در روش Vigenère و رمزگشایی با استفاده از شیوهٔ رمزنگاری در Vigenère است. از این روش با نام Variant Beaufort یاد می‌شود. این روش متفاوت از رمزگذاری Beoufort[12] است، ساخته شده توسط Francis Beoufort، که شبیه Vigenère است اما از یک مکانیزم رمزگذاری و جدول کمی تغییر یافته استفاده می‌کند. رمزگذاری Beoufort یک رمزنگاری متقارن است.

علیرغم قدرت رمزنگاری Vigenère، هرگز در اروپا مورد استفاده گسترده قرار نگرفت. رمزنگاری Gronsfeld نوعی دیگر از رمزنگاری است که توسط Count Gronsfeld ایجاد شده‌است. مشابه رمزنگاری Vigenère است با این تفاوت که تنها از ۱۰ الفبای رمزنگاری مختلف استفاده می‌کند، رقم‌های ۰ تا ۹). یک کلید Gronsfeld، ۰۱۲۳ همان کلید Vigenere , ABCD است. رمزنگاری Gronsfeld از این مزیت را دارد که کلید آن یک کلمه نیست، و ضعف آن این است که ۱۰ الفبای رمز دارد. این رمز Gronsfeld است که علی‌رغم نقاط ضعف آن، در سراسر آلمان و اروپا مورد استفاده گسترده قرار گرفت.

کد

---

# Python code to implement
# Vigenere Cipher
# This function generates the
# key in a cyclic manner until
# it's length isn't equal to
# the length of original text
def generateKey(string, key):
    key = list(key)
    if len(string) == len(key):
        return(key)
    else:
        for i in range(len(string) -
                    len(key)):
            key.append(key[i % len(key)])
    return("" . join(key))
# This function returns the
# encrypted text generated
# with the help of the key
def cipherText(string, key):
    cipher_text = []
    for i in range(len(string)):
        x = (ord(string[i]) +
            ord(key[i])) % 26
        x += ord('A')
        cipher_text.append(chr(x))
    return("" . join(cipher_text))
# This function decrypts the
# encrypted text and returns
# the original text
def originalText(cipher_text, key):
    orig_text = []
    for i in range(len(cipher_text)):
        x = (ord(cipher_text[i]) -
            ord(key[i]) + 26) % 26
        x += ord('A')
        orig_text.append(chr(x))
    return("" . join(orig_text))
# Driver code
if __name__ == __main__":
    string = "GEEKSFORGEEKS"
    keyword = "AYUSH"
    key = generateKey(string, keyword)
    cipher_text = cipherText(string,key)
    print("Ciphertext :", cipher_text)
    print("Original/Decrypted Text :",
        originalText(cipher_text, key))

منابع

1. «substitution».
2. «Giovan_Battista_Bellaso».
3. «Friedrich_Kasiski».
4. «Blaise_de_Vigen».
5. «re_square_shading».
6. «One-time_pad».
7. «Caesar_cipher».
8. «Caesar_cipher».
9. «Charles_Babbage».
10. «William_F._Friedman».
11. «Autokey_cipher».
12. «Beaufort_cipher».

Vigenère cipher