سامانه لورنتس

سیستم لورنتس (به انگلیسی: Lorenz system) یک سیستم معادلات دیفرانسیل معمولی است که برای اولین بار توسط ادوارد لورنتس و الن فتر مورد بررسی قرار گرفت. برای داشتن راه حل‌های برای مقادیر خاص پارامتر و شرایط اولیه نظریه آشوب قابل توجه است. به شکل خاص، جاذب لورنتس مجموعه‌ای از راه حل‌های بی‌نظم سیستم لورنتس است. بر پایه مقالات منتشره در رسانه‌های مشهور، «اثر پروانه‌ای» از پیامدهای واقعی جاذب لورنتس ناشی می‌شود، یعنی در هر سیستم فیزیکی، در صورت عدم دانش کامل از شرایط اولیه (حتی تغییرات کوچک هوا به دلیل بال زدن پروانه)، عملاً توانایی ما در پیش‌بینی مسیر آینده آن همیشه شکست خواهد خورد. در این سیستم تأکید می‌شود که سیستم‌های فیزیکی می‌توانند کاملاً قطعی باشند و در عین حال حتی در غیاب اثرات کوانتومی نیز ذاتاً قابل پیش‌بینی نباشند. شکل جاذب لورنتس نیز در صورت ترسیم گرافیکی، ممکن است شبیه یک پروانه باشد.

یک شمای نمونه در جاذب لورنتس وقتی که ρ = ۲۸، σ = ۱۰ و ۳/۸ = β باشد

بررسی اجمالی

در سال ۱۹۶۳، ادوارد لورنتس، با کمک الن فتر، یک مدل ریاضی ساده برای همرفت جوی ایجاد کرد.[1] این مدل سیستمی از سه معادله دیفرانسیل معمولی تشکیل شده‌است که اکنون به عنوان معادلات لورنتس شناخته می‌شوند:

معادلات لورنتس نیز در مدل‌های ساده شده برای لیزر،[2] مولد الکتریکی،[3] ترموسیفون،[4] موتور جریان مستقیم،[5] مدار الکتریکی،[6] واکنش‌های شیمیایی[7] و اسمز مستقیم کاربرد دارد.[8] این معادلات همچنین از معادلات مطرح در فضای فوریه برای چرخ آب مالکوس هستند.[9][10] چرخ آب مالکوس حرکت آشفته‌ای را به نمایش می‌گذارد که در آن به جای چرخش در یک جهت با سرعت ثابت، چرخشی با سرعت متناوب، کندی، توقف، تغییر جهت‌ها و نوسان به جلو و عقب یا ترکیبی از چنین رفتاری را به روشی غیرقابل پیش‌بینی دارد.

از نظر فنی، سیستم لورنتس غیرخطی، غیر دوره ای، سه بعدی و قطعی است. معادلات لورنتس موضوع صدها مقاله تحقیقاتی و حداقل یک کتاب بوده‌است.[11]

تحلیل و بررسی

به شکل پیش‌فرض پارامترها ، ، و مثبت هستند لورنتس از مقادیر ، و استفاده کرد. این سیستم رفتارهای آشفته‌ای را برای این مقادیر (و نزدیک به آن) نشان می‌دهد.[12]

اگر پس فقط یک نقطه تعادل وجود دارد که در مبدأ است. این نقطه با عدم همرفت مطابقت دارد. همه معادلات زمانی درست است، که عدد یک جاذب جهانی است .[13]

انشعاب چنگال در ، و برای دو نقطه مهم اضافی در: و اینها مربوط به همرفت ثابت هستند. این جفت نقطه تعادل فقط در صورت ثبات است

فقط می‌تواند مثبت باشد اگر . در مقدار بحرانی، هر دو نقطه تعادل ثبات را از طریق انشعاب هاپ زیر بحرانی از دست می‌دهند.[14]

هنگامی ، ، و ، سیستم لورنتس دارای نتایج بی نظم است (اما همه نتایج هرج و مرج نیستند). تقریباً تمام نقاط اولیه به یک مجموعه ثابت تغییر می‌کنند.

تجزیه و تحلیل جاذب لورنتس دشوار است، اما عملکرد معادله دیفرانسیل بر روی جاذب توسط یک مدل هندسی نسبتاً ساده است.[15] اثبات این که واقعاً چنین است چهاردهمین مشکل در لیست مسائل اسمیل است. این مشکل اولین مشکلی بود که توسط وارویک تاکر در سال ۲۰۰۲ حل شد.[16]

برای سایر مقادیر ، این سیستم مدارهای دورانی گره خورده را نمایش می‌دهد. مثلاً با به یک گره توروس تی(۳،۲) تبدیل می‌شود.

راه حل‌های نمونه ای از سیستم لورنتس برای مقادیر مختلف ρ
ρ = ۱۴، σ = ۱۰، β = ۸/۳ ρ = ۱۳، σ = ۱۰، β = ۸/۳
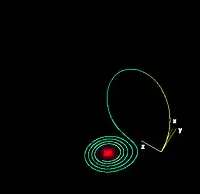ρ = ۱۵، σ = ۱۰، β = ۸/۳ ρ = ۲۸، σ = ۱۰، β = ۸/۳
برای مقادیر کوچک ρ، سیستم پایدار است و به یکی از دو جاذب نقطه ثابت تبدیل می‌شود. وقتی ρ از ۲۴٫۷۴ بزرگتر باشد، نقاط ثابت دافعه می‌شوند و مسیر توسط آنها به روشی کاملاً پیچیده دفع می‌شود.
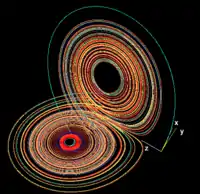
وابستگی حساس به شرایط اولیه
زمان t = ۱ زمان t = ۲ زمان t = ۳
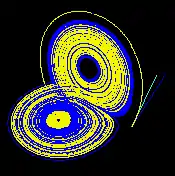این ارقام - ساخته شده با استفاده از ρ = ۲۸، σ = ۱۰ و β = ۸/۳ - سه بخش زمانی از تکامل 3-D دو مسیر را نشان می‌دهد (یکی به رنگ آبی، دیگری به زرد) در جاذب لورنتس با شروع از دو اولیه نقاطی که فقط با ۵-۱۰ در مختصات x متفاوت هستند. در ابتدا به نظر می‌رسد که این دو مسیر همزمان هستند (فقط یک زرد دیده می‌شود، زیرا روی یک مسیر آبی کشیده شده‌است) اما پس از مدتی واگرایی واضح است.

شبیه‌سازی‌ها

شبیه‌سازی متلب

 
% Solve over time interval [0,100] with initial conditions [1,1,1]
% ''f'' is set of differential equations
% ''a'' is array containing x, y, and z variables
% ''t'' is time variable

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
[t,a] = ode45(f,[0 100],[1 1 1]); % Runge-Kutta 4th/5th order ODE solver
plot3(a(:,1),a(:,2),a(:,3))

شبیه‌سازی ریاضیات

روش استاندارد:

tend = 50;
eq = {x'[t] == σ (y[t] - x[t]),
      y'[t] == x[t] (ρ - z[t]) - y[t],
      z'[t] == x[t] y[t] - β z[t]};
init = {x[0] == 10, y[0] == 10, z[0] == 10};
pars = {σ->10, ρ->28, β->8/3};
{xs, ys, zs} =
  NDSolveValue[{eq /. pars, init}, {x, y, z}, {t, 0, tend}];
ParametricPlot3D[{xs[t], ys[t], zs[t]}, {t, 0, tend}]

کمتر صریح:

lorenz = NonlinearStateSpaceModel[{{σ (y - x), x (ρ - z) - y, x y - β z}, {}}, {x, y, z}, {σ, ρ, β}];
soln[t_] = StateResponse[{lorenz, {10, 10, 10}}, {10, 28, 8/3}, {t, 0, 50}];
ParametricPlot3D[soln[t], {t, 0, 50}]

راه حل تعاملی به صورت پویا:

eqs = {
  x'[t] == σ (y[t] - x[t]), y'[t] == x[t] (ρ - z[t]) - y[t], z'[t] == x[t] y[t] - β z[t],
  x[0] == 10, y[0] == 10, z[0] == 10
};
tmax = 50;
sol = ParametricNDSolveValue[eqs, Function[t, {x[t], y[t], z[t]}], {t, 0, tmax}, {σ, ρ, β}];
Manipulate[
  fun = sol[σ, ρ, β];
  plot = ParametricPlot3D[fun[t], {t, 0, tmax}, PlotRange -> All, PerformanceGoal -> "Quality"];
  Animate[
    Show[plot, Graphics3D[{PointSize[0.05], Red, Point[fun[t]]}]],
    {t, 0, tmax}, AnimationRunning -> True, AnimationRate -> 1
  ],
  {{σ, 10}, 0, 100}, {{ρ, 28}, 0, 100}, {{β, 8/3}, 0, 100},
  TrackedSymbols :> {σ, ρ, β}
]

شبیه‌سازی پایتون

 
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D

rho = 28.0
sigma = 10.0
beta = 8.0 / 3.0

def f(state, t):
    x, y, z = state  # Unpack the state vector
    return sigma * (y - x), x * (rho - z) - y, x * y - beta * z  # Derivatives

state0 = [1.0, 1.0, 1.0]
t = np.arange(0.0, 40.0, 0.01)

states = odeint(f, state0, t)

fig = plt.figure()
ax = fig.gca(projection="3d")
ax.plot(states[:, 0], states[:, 1], states[:, 2])
plt.draw()
plt.show()

شبیه‌سازی مدلینگ

 
model LorenzSystem

  parameter Real sigma = 10;
  parameter Real rho = 28;
  parameter Real beta = 8/3;

  parameter Real x_start = 1 "Initial x-coordinate";
  parameter Real y_start = 1 "Initial y-coordinate";
  parameter Real z_start = 1 "Initial z-coordinate";

  Real x "x-coordinate";
  Real y "y-coordinate";
  Real z "z-coordinate";

initial equation
  x = x_start;
  y = y_start;
  z = z_start;

equation

  der(x) = sigma*(y-x);
  der(y) = rho*x - y - x*z;
  der(z) = x*y - beta*z;

end LorenzSystem;

شبیه‌سازی جولیا

 
using DifferentialEquations, ParameterizedFunctions, Plots

lorenz = @ode_def begin # define the system
 dx = σ * (y - x)
 dy = x * (ρ - z) - y
 dz = x * y - β*z
end σ ρ β

u0 = [1.0,0.0,0.0] # initial conditions
tspan = (0.0,100.0) # timespan
p = [10.0,28.0,8/3] # parameters
prob = ODEProblem(lorenz, u0, tspan, p) # define the problem
sol = solve(prob) # solve it
plot(sol, vars = (1, 2, 3)) # plot solution in phase space - variables ordered with 1 based indexing

شبیه‌سازی ماکسیما

 
load(dynamics)$
load(draw)$

/* System parameters */
a: 10; b: 8/3; r: 28;

lorenzSystem: [a*(y-x), -x*z+r*x-y, x*y-b*z];
dependentVariables: [x, y, z]$
initialValues: [1, 1, 1]$
timeRange: [t, 0, 50, 0.01]$

/* solution via 4th order Runge-Kutta method */
systemSolution: rk(lorenzSystem, dependentVariables, initialValues, timeRange)$
solutionPoints: map(lambda([x], rest(x)), systemSolution)$

draw3d(point_type=none, points_joined=true, color=blue,
       xlabel="x(t)", ylabel="y(t)", zlabel="z(t)",
       points(solutionPoints));

استخراج معادلات لورنتس به عنوان مدلی برای همرفت جوی

معادلات لورنتس از تقریب بوسینسک (شناوری) به معادلات توصیف گردش سیال در یک لایه کم عمق مایع مشتق شده‌است، هنگامی مایع از پایین به‌طور یکنواخت گرم می‌شود و از بالا به‌طور یکنواخت سرد می‌شود.[1] این گردش سیال به همرفت ریلی–بنارد معروف است. مفروض است که مایع در دو بعد (عمودی و افقی) با شرایط مرزی مستطیلی شکل گردش می‌کند.[17]

مشارکت‌ها

لورنتس مشارکت‌های الن فتر را در مقاله خود، که مسئول شبیه‌سازی‌های عددی و ارقام است، تأیید می‌کند.[1] همچنین، مارگارت همیلتون در محاسبات عددی اولیه و منجر به یافته‌های مدل لورنتس کمک کرد.[18]

نگارخانه
  • یک راه حل در جاذب لورنز با وضوح بالا در صفحه xz رسم شده‌است.
  • یک راه حل در جاذبه‌های لورنز به عنوان SVG ارائه شده‌است.
  • یک راه حل در جاذب لورنز به عنوان یک سیم فلزی برای نشان دادن جهت و ساختار سه بعدی ارائه شده‌است.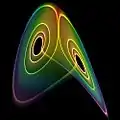
  • تصویری از جاذب لورنز در نزدیکی یک چرخه متناوب.
  • دو خط ساده در سیستم لورنز ، از rho = ۰ تا rho = ۲۸ (سیگما = ۱۰ ، بتا = ۸/۳)
  • انیمیشن یک سیستم لورنز با وابستگی روحی

پانویس
  1. Lorenz (1963)
  2. Haken (1975)
  3. Knobloch (1981)
  4. Gorman, Widmann & Robbins (1986)
  5. Hemati (1994)
  6. Cuomo & Oppenheim (1993)
  7. Poland (1993)
  8. Tzenov (2014)
  9. Kolář & Gumbs (1992)
  10. Mishra & Sanghi (2006)
  11. Sparrow (1982)
  12. Hirsch, Smale & Devaney (2003), pp. 303–305
  13. Hirsch, Smale & Devaney (2003), pp. 306+307
  14. Hirsch, Smale & Devaney (2003), pp. 307+308
  15. Guckenheimer, John; Williams, R. F. (1979-12-01). "Structural stability of Lorenz attractors". Publications Mathématiques de l'Institut des Hautes Études Scientifiques. 50 (1): 59–72. doi:10.1007/BF02684769. ISSN 0073-8301.
  16. Tucker (2002)
  17. Hilborn (2000), Appendix C; Bergé, Pomeau & Vidal (1984), Appendix D
  18. Lorenz (1960)

منابع

برای مطالعهٔ بیشتر

پیوند به بیرون

  • "Lorenz attractor"، دانشنامه ریاضیات، EMS Press، ۲۰۰۱ [۱۹۹۴]
  • Weisstein, Eric W. "جذب کننده لورنز". MathWorld.
  • جذب کننده لورنز توسط راب موریس، پروژه تظاهرات ولفرام.
  • معادله لورنز در planetmath.org
  • هرج و مرج همزمان و ارتباطات خصوصی ، با کوین کوومو. اجرای جاذب لورنز در یک مدار الکترونیکی.
  • انیمیشن تعاملی Lorenz جذب کننده (به پلاگین Adobe Shockwave نیاز دارید)
  • 3D Attractors: برنامه Mac برای تجسم و کشف جذابیت لورنز در ۳ بعد
  • Lorenz Attractor در الکترونیکی آنالوگ اجرا شده‌است
  • انیمیشن تعاملی Lorenz Attractor (اجرا شده در آدا با GTK +). منابع و قابل اجرا)
  • Lorenz Attractor مبتنی بر وب (اجرا شده در JavaScript / HTML / CSS)
  • وب مبتنی بر تعامل Lorenz Attractor ساخته شده با یدید
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.