شاخص میلر

شاخص میلر (به انگلیسی: Miller Index) در بلورشناسی روشی برای مشخص کردن صفحات در شبکه براوه است. به‌طور مشخص خانواده‌ای از صفحات بلوری با سه عدد صحیح k, h و l مشخص می‌شوند که به صورت (hkl) نوشته می‌شود.

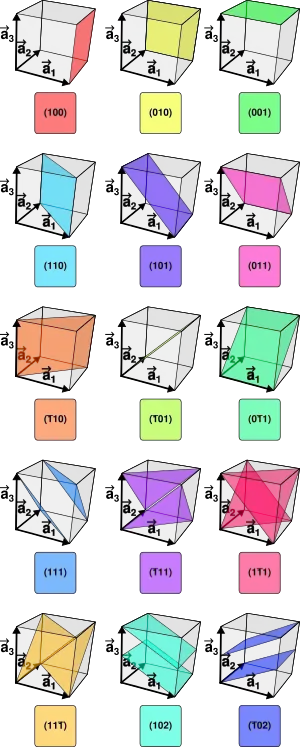
صفحاتی با شاخص میلر متفاوت در بلور مکعبی

شاخص میلر یک سیستم نماد در کریستالوگرافی برای سطوح هموار در تشکیل شبکه‌ها را نشان می‌دهد.

به‌طور خاص، میلر یک گروه از شبکه‌های سطوح هموار را با سه عدد صحیح h,kوl مشخص می‌کنند. (توجه داشته باشید که سطوح هموار همیشه بر خطوط ترکیبی که مستقیم به شبکه‌های بردار عمود نیست زیرا بردارهای شبکه متقابل نیاز به عمود بودن را ندارد) اعدادصحیح معمولاً در ساده‌ترین شرایط نوشته می‌شوند، براساس قرارداد اعداد صحیح منفی توسط یک نوار ۳*۳ نوشته می‌شود. به عنوان مثال بزرگ‌ترین مقسوم علیه مشترک آن‌ها باید یک باشد. همچنین چندین نمادهای مرتبط وجود دارد: نماد{hkl}مجموعه‌ای از شبکه‌هایی را نشان می‌دهد که توسط تقارن شبکه مساوی با (hkl)هستند.

شاخص‌های میلر در سال ۱۸۳۹ توسط معدن‌شناس بریتانیایی ویلیام هالورز میلر معرفی شدند که این روش نیز در طول تاریخ به عنوان سیستم millerion شناخته می‌شود نمونه‌هایی از تعیین شاخص یک شبکه با استفاده از محور چپ (۱۱۱) وراست (۱۱۲) مشخص شده‌اند. دو راه معادل تعریف شاخص میلر وجود دارد، از طریق یک نقطه در شبکه متقابل یا به عنوان جداکننده معکوس بردارهای شبکه، هر دو تعریف در زیر آورده شده‌است، بردار شبکه نیاز به انتخاب هر سه مورد a1, a2, a3 را دارد که نشان دهندهٔ سلول واحد می‌باشد (توجه داشته باشید که سلول واحد معمولی ممکن است بزرگتر از سلول واحد شبکه براوه به عنوان نمونه‌هایی که در زیر تعریف شده‌است) توجه به این سه بردار اولیه عمودی نشان دهندهٔ شبکه متقابل (علائمb1, b2, b3) است. با توجه به سطح شاخص میلر h,k،l علائم سطوح متقابل بر بردار شبکه عمود است. از آن جاییکه مختصات اعداد (hkl) به سادگی یک شبکه معمولی براساس بردارهای اولیه متقابل را نشان می‌دهد. بدان معناست که اعداد صحیح همپایه، همیشه یک بردار شبکهٔ متقابل را دارند و همچنین نیاز به کمترین زمان بدان معناست که بردار شبکه متقابل در کوتاه‌ترین حالت جهت داده شده‌است. بدین ترتیب، علائم (h,k,l) سطوح همواری را که جداکننده سه نقطه a1/h, a2/k, a3/ℓ, یا چندین نقطه که متعلق به آن است را نشان می‌دهد. بدان معنی است که نمادهای میلر تناسبی نسبی به جداکننده‌های معکوس سطوح هموار بر اساس بردارهای شبکه دارند. اگر یکی از شاخص‌ها صفر باشد، بدان معناست که شبکه‌ها محورها را قطع نمی‌کنند. با توجه به اینکه تنها سطوح هموار (h,k,l) یک نقطه یا بیشتر از (سطوح شبکه) را قطع نمی‌کند، مساحت مجاور عمود بر d بین سطوح شبکه که مربوط به کوتاه‌ترین بردار عمودی متقابل به شبکه‌ها می‌باشد فرموله شده‌است: بدان معناست که پایه شبکه مستقیم به جای شبکه متقابل استفاده می‌شود. توجه داشته باشید که [hkℓ] نسبت به شبکه‌های (hkℓ) متداول نیست، به جز در شبکه‌های مکعبی که در زیر توضیح داده می‌شود.

سازه مکعبی

در مورد خاصی از کریستال ساده مکعب، بردارهای شبکه عمود و با طول یکسان (معمولاً با علامت a بیان می‌شود) و به عنوان شبکه متقابل هستند؛ بنابراین، در این مورد مشترک'''شاخص‌های میلر''' (hkℓ) و [hkℓ] هر دو به سادگی به‌طور نرمال به مختصات دکارتی دلالت دارند. در کریستال‌های مکعب با فواصل شبکه a، فضای d بین سطوح همجوار (hkℓ) از بالا می‌باشد. به دلیل تقارن کریستال‌های مکعب، این امکان تغییر مکان و علائم اعداد صحیح وجود دارد و همچنین سطوح هموار جهت مستقیم و یکسان داشته باشند: • نماها در زاویه پرانتز مانند ⟨۱۰۰⟩ مجموعه جهت داری که بر اساس ساختار تقارن یکسان هستند اشاره می‌کند، همانند [۱۰۰], [۰۱۰], [۰۰۱] ویا منفی هریک از این جهات. • نماها در پرانتز حلقوی یا کروشه‌ها مثل {۱۰۰}مجموعه‌ای از سطح هموار معمولی را که بر اساس ساختار تقارن یکسان هستند، با این حال تعدادی از پرانتزهای زاویه یک مجموعه جهت دار را نشان می‌دهد. • بردارهای شبکه بدوی و بردارهای توری مکعبی، عمود بر شبکه بردار نیستند. هرچند در این مورد شاخص‌های میلر به‌طور قراردادی مربوط به بردارهای شبکه مکعبی هستند و در نتیجه دوباره دلالت بر مختصات دکارتی دارند.

سازه‌های شش ضلعی و رو مبو هدرال

سازه‌های شش ضلعی و رو مبو هدرال ممکن است با استفاده از سیستم میلر که در چهار شاخص (hkil)مورد استفاده قرار گیرد. در اینجا h,k،lمربوط به شاخص میلر هستند و i یک شاخص برکنار شده‌است. این چهار شاخص برای برچسب زدن سطوح هموار در یک شبکه شش ضلعی متقارن جانشین مشخصی می‌باشد. به عنوان مثال شباهت بین (۱۲۱۰)=(۱۲۰) و (۱۱۲۰)=(۱۱۰)آشکارتر است وقتیکه شاخص برکنار شده نشان داده می‌شود. به عنوان مثال:بردار شبکه متقابل وhkl به عنوان بردارهای شبکه متقابل که در بالا پیشنهاد شده‌است استفاده می‌شود. برای کریستال‌های شش ضلعی ممکن است بردارهای پایه شبکه جهت دار a1،a2،a3 بیان شود. در نتیجه در شکل سه‌گانه نرمال، به سادگی (hkl) از شاخص منطقه عمود بر صفحه استفاده می‌شود. همان‌طور که می‌بینید در منطقه چهار شاخص در مربع یا زاویه گاهی اوقات یک شاخص مستقیم شبکه تنها در سمت راست با شاخص‌های شبکه در سمت چپ ترکیب می‌شوند

منابع

    مشارکت‌کنندگان ویکی‌پدیا. «Miller index». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ دسامبر ۲۰۱۳.

    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.