قضیه استوارت

قضیه استوارت، (به انگلیسی: Stewart's theorem) در هندسه اندازه پاره‌خط وارد از یک رأس بر ضلع روبرو را بر حسب اندازه اضلاع مثلث و دو پاره‌خط ایجاد شده بر روی ضلع می‌دهد. به افتخار ریاضیدان اسکاتلندی متیو استوارت که در مقاله‌ای در سال ۱۷۴۸ این قضیه را منتشر کرد، این قضیه را قضیه استوارت نامیده‌اند.[1]

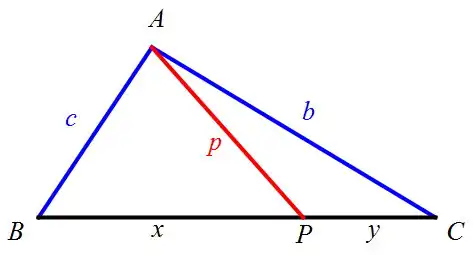
(قضیۀ استوارت)؛ در مثلث ABC، پاره خط AP را از رأس A به یکی از نقاط دلخواه P در ضلع BC چنان رسم می‌کنیم که آن را به نسبت x و y قطع کند.

اگر b ،a و c طول اضلاع مثلت و p طول پاره خط مورد نظر باشد، آنگاه:

${\displaystyle a(p^{2}+xy)=b^{2}x+c^{2}y\,}$ و یا:

${\displaystyle ap^{2}=b^{2}x+c^{2}y-axy\,}$

که x و y طول دو پاره‌خط ایجاد شده بر ضلع هستند.

اثبات

اگر محل برخورد پاره‌خط p و ضلع BC را P بنامیم، آنگاه بنابر قانون کسینوس‌ها برای دو زاویه APB و APC داریم:

${\displaystyle b^{2}=p^{2}+y^{2}-2py\cos {\theta }\,}$

${\displaystyle c^{2}=p^{2}+x^{2}+2px\cos {\theta }\,}$

با ضرب کردن x در جمله اول و y در جمله دوم معادلات زیر بدست می‌آید:

${\displaystyle xb^{2}=xp^{2}+xy^{2}-2pxy\cos {\theta }\,}$

${\displaystyle yc^{2}=yp^{2}+yx^{2}+2pxy\cos {\theta }\,}$

حال با جمع کردن دو معادله بالا بدست می‌آید:

${\displaystyle xb^{2}+yc^{2}=(x+y)p^{2}+xy(x+y)\,}$

که همان معادله قضیه استوارت است.

منابع

1. M. Stewart Some General Theorems of Considerable Use in the Higher Parts of Mathematics (1746) "Proposition II"

• مشارکت‌کنندگان ویکی‌پدیا. «Stewart's theorem». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۰ ژوئیه ۲۰۰۸.