قضیه اصلی واکاوی الگوریتم‌ها

قضیه اصلی واکاوی (تحلیل) الگوریتم‌ها که حالتی خاص از روش اکرا-بازی در تحلیل الگوریتم‌ها است ، یک راه حل سرراست برای حالت‌های مجانبی که در عمل برای حل انواع روابط بازگشتی رخ می‌دهند، ارائه می‌کند. این قضیه با کتاب درسی معروف مقدمه‌ای بر الگوریتم‌ها نوشتهٔ کرمن، لیسرسن، ریوست و استین به شهرت رسید. این قضیه در بخش ۴٫۳ دراین کتاب معرفی شده‌است و متعاقباً در بخش ۴٫۴ به اثبات رسیده‌است. هرچند که نمی‌توان تمامی روابط بازگشتی را به کمک قضیهٔ اصلی حل کرد.

نسخه دست نویس استین

شکل کلی

قضیهٔ اصلی روابطی را مورد بررسی قرار می‌دهد که به شکل زیر باشند:

${\displaystyle T(n)=a\;T\!\left({\frac {n}{b}}\right)+f(n)\;\;\;\;{\mbox{where}}\;\;a\geq 1{\mbox{, }}b>1.}$

معنای علائم به کار رفته در استفاده از رابطهٔ فوق برای یک الگوریتم بازگشتی، به شرح زیر است: *n اندازهٔ مسئله‌است.

a تعداد زیرمسئله هاست.

• n/b اندازهٔ هر یک از زیرمسئله هاست. (در اینجا فرض شده‌است که اندازهٔ همهٔ زیرمسئله‌ها با هم برابر است.)
• (f(n هزینهٔ بخش غیر بازگشتی است که شامل هزینهٔ تقسیم مسئله به زیرمسئله‌ها و هزینهٔ ادغام پاسخ به زیرمسئله هاست.

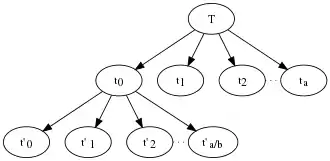
الگوریتم فوق به صورت بازگشتی مساله را به تعدادی از زیرشاخه ها تقسیم می کند که هر یک از مسایل فرعی با اندازه ( n / b ) است . درخت حل آن گره ای برای هر تماس بازگشتی دارد که فرزندان آن گره سایر تماس های حاصل از آن تماس هستند. برگهای درخت موارد اصلی بازگشت هستند ، مقادیر کوچک (از اندازه کمتر از k) که برگشت نمی کنند.

قضیه اصلی واکاوی غالباً مرزهایی را به صورت نامتعارفی به برخی از الگوریتم های تقسیم و به صورت بازگشتی می دهد که یک پارتیشن ورودی را به مقادیر کوچکتر با اندازه های مساوی تقسیم می کند ، مقادیر کوچک فرعی را به صورت بازگشتی حل می کند ، و سپس راه حل های فرعی را با هم ترکیب می کند تا راه حلی برای مسئله اصلی ارائه دهد. زمان چنین الگوریتمی را می توان با اضافه کردن کارهایی که در سطح بالای بازگشت آنها (برای تقسیم مشکلات در زیرمجموعه ها و سپس ترکیب راه حل های فرعی) بیان شده و همزمان با زمان انجام شده در تماس های بازگشتی الگوریتم,انجام می دهند.

طبق قضیه اصلی سه حالت داریم :

1. f(n) = Θ(n^c) در حالی که c < Log_ba نتیجه می شود T(n) = Θ(n^Log_ba)

2. If f(n) = Θ(n^c) در حالی که c = Log_ba نتیجه می شود T(n) = Θ(n^cLog n)

3.If f(n) = Θ(n^c) در حالی کهc > Log_ba نتیجه می شود T(n) = Θ(f(n))

در سه حالت می‌توان یک حد مجانبی مشخص کرد:

حالت ۱

شکل کلی

اگر شرط ${\displaystyle \epsilon >0}$ وجود داشته باشد به طوری که رابطهٔ ${\displaystyle f(n)={\mathcal {O}}\left(n^{\log _{b}\left(a\right)-\epsilon }\right)}$ برقرار باشد،

درخت راه حل

آن گاه داریم:

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\right).}$

مثال اول

${\displaystyle T(n)=8T\left({\frac {n}{2}}\right)+1000n^{2}}$

همان طور که در فرمول فوق دیده می‌شود، متغیرها دارای مقادیر زیر هستند:

${\displaystyle a=8\,}$، ${\displaystyle b=2\,}$، ${\displaystyle f(n)=1000n^{2}\,}$، ${\displaystyle \log _{b}a=\log _{2}8=3\,}$

حال باید برقراری معادلهٔ زیر را بررسی کنیم:

${\displaystyle f(n)={\mathcal {O}}\left(n^{\log _{b}a-\epsilon }\right)}$

اگر مقادیر متغیرها را در این رابطه جایگزین کنیم، خواهیم داشت:

درخت بازگشت

${\displaystyle 1000n^{2}={\mathcal {O}}\left(n^{3-\epsilon }\right)}$

با انتخاب ${\displaystyle \epsilon =1}$ داریم:

${\displaystyle 1000n^{2}={\mathcal {O}}\left(n^{3-1}\right)={\mathcal {O}}\left(n^{2}\right)}$

از آن جایی که معادلهٔ بالا برقرار است، حالت اول قضیهٔ اصلی را برای رابطهٔ بازگشتی به کار می‌بریم و از نتیجهٔ زیر استفاده می‌کنیم:

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\right).}$

اگر مقادیر فوق را در رابطهٔ بالا قرار دهیم، در نهایت خواهیم داشت:

${\displaystyle T(n)=\Theta \left(n^{3}\right).}$

از این رو رابطهٔ بازگشتی داده شده (T(n از(Θ(n³ است.

(راه حل دقیق رابطهٔ بازگشتی نیز این نتیجه را تأیید می‌کند، که در آن ${\displaystyle T(n)=1001n^{3}-1000n^{2}}$، بافرض ${\displaystyle T(1)=1}$ است.)

• حالت ۲

شکل کلی

اگر داشته باشیم:

${\displaystyle \exists k\geq 0,f(n)=\Theta \left(n^{\log _{b}a}\log ^{k}\right)}$

آن گاه خواهیم داشت:

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\log ^{k+1}\right).}$

مثال

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+10n}$

همان طور که در فرمول فوق مشاهده می‌شود، متغیرها مقادیر زیر را اختیار می‌کنند:

${\displaystyle a=2\,}$، ${\displaystyle b=2\,}$، ${\displaystyle k=0\,}$، ${\displaystyle f(n)=10n\,}$، ${\displaystyle \log _{b}a=\log _{2}2=1\,}$

حال می‌بایست برقراری رابطهٔ زیر را بررسی کنیم (در حالتی که k=۰ باشد):

درخت راه حل

${\displaystyle f(n)=\Theta \left(n^{\log _{b}a}\right)}$

اگر مفادیر متغیرها را،از رابطهٔ بالا در این رابطه جایگزین کنیم، خواهیم داشت:

${\displaystyle 10n=\Theta \left(n^{1}\right)=\Theta \left(n\right)}$

از آن جایی که این رابطه برقرار است، حالت دوم قضیهٔ اصلی را برای رابطهٔ بازگشنی به کار می‌بریم و از نتیجهٔ زیر استفاده می‌کنیم:

${\displaystyle T(n)=\Theta \left(n^{\log _{b}a}\log n\right).}$

با جایگزین کردن مقادیر فوق در این رابطه در نهایت خواهیم داشت:

${\displaystyle T(n)=\Theta \left(n\log n\right).}$

از این رو رابطهٔ بازگشتی داده شدهٔ (T(n از (Θ(n log n است.

(راه حل دقیق رابطهٔ بازگشتی نیز این نتیجه را تأیید می‌کند، که در آن ${\displaystyle T(n)=n+10n\log _{2}n}$، بافرض ${\displaystyle T(1)=1}$ است.)

حالت ۳

شکل کلی

اگر شرط ${\displaystyle \epsilon >0}$ وجود داشته باشد به طوری که رابطهٔ ${\displaystyle f(n)=\Omega \left(n^{\log _{b}a+\epsilon }\right)}$ برقرار باشد و همچنین اگر برای nهای به اندازهٔ کافی بزرگ ثابت ${\displaystyle c<1}$ وجود داشته باشد به گونه‌ای که رابطه زیر برقرار باشد:

${\displaystyle af\left({\frac {n}{b}}\right)\leq cf(n)}$

آنگاه خواهیم داشت:

${\displaystyle T\left(n\right)=\Theta \left(f\left(n\right)\right).}$

مثال

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+n^{2}}$

همان طور که در فرمول فوق دیده می‌شود، متغیرها مقادیر زیر را اختیار می‌کنند:

${\displaystyle a=2\,}$، ${\displaystyle b=2\,}$، ${\displaystyle f(n)=n^{2}\,}$، ${\displaystyle \log _{b}a=\log _{2}2=1\,}$

حال می‌بایست برقراری معادلهٔ زیر را مورد بررسی قرار دهیم:

${\displaystyle f(n)=\Omega \left(n^{\log _{b}a+\epsilon }\right)}$

اگر مقادیر متغیرها را طبق روابط بالا قرار دهیم و مقدار ${\displaystyle \epsilon =1}$ را انتخاب کنیم، خواهیم داشت:

${\displaystyle n^{2}=\Omega \left(n^{1+1}\right)=\Omega \left(n^{2}\right)}$

از آن جایی که معادلهٔ فوق برقرار است، حال باید شرط دوم را مورد بررسی قرار دهیم. به عبارت دیگر باید درستی رابطهٔ زیر را مورد بررسی قرار دهیم:

${\displaystyle af\left({\frac {n}{b}}\right)\leq cf(n)}$

اگر بار دیگر مقادیر متغیرها را طبق روابط بالا قرار دهیم، خواهیم داشت:

${\displaystyle \leq cn^{2}\Leftrightarrow {\frac {1}{2}}n^{2}\leq cn^{2}}$ ${\displaystyle 2\left({\frac {n}{2}}\right)^{2}}$

اگر ${\displaystyle c={\frac {1}{2}}}$ را برگزینیم، آن گاه:

${\displaystyle \forall n\geq 1}$ ${\displaystyle {\frac {1}{2}}n^{2}\leq {\frac {1}{2}}n^{2}}$

پس خواهیم داشت:

${\displaystyle T\left(n\right)=\Theta \left(f\left(n\right)\right).}$

اگر بار دیگر مقادیر لازم را قرار دهیم، رابطهٔ زیر به دست می‌آید:

${\displaystyle T\left(n\right)=\Theta \left(n^{2}\right).}$

از این رو رابطهٔ بازگشتی داده شده (T(n از (Θ(n² است.

(راه حل دقیق رابطهٔ بازگشتی نیز این نتیجه را تأیید می‌کند، که در آن ${\displaystyle T(n)=2n^{2}-n}$، بافرض ${\displaystyle T(1)=1}$ است.)

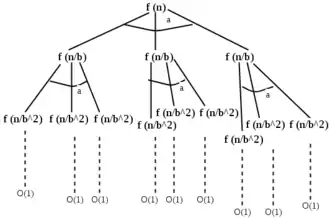
در روش درخت بازگشتی ، کل کارهای انجام شده را محاسبه می کنیم. اگر کارهایی که در برگها انجام می شود چند جمله ای بیشتری است ، پس برگها قسمت اصلی هستند و نتیجه ما به کارهایی که در برگها انجام می شود تبدیل می شود (حالت 1). اگر کارهایی که در برگ و ریشه انجام می شود به صورت یکسان باشد ، نتیجه کار ما با کارهایی که در هر سطح انجام می شود ضرب می شود (حالت 2). اگر کارهایی که در ریشه انجام می شوند بیشتر از لحاظ غیرمتعارف باشند ، نتیجه ما به کارهایی در ریشه انجام می شود (حالت 3).

قضیه اصلی

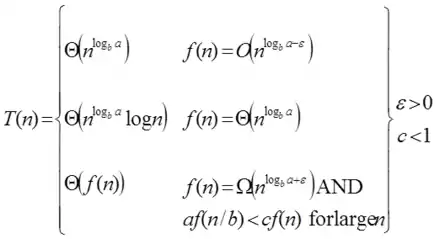
حالت‌های ناپذیرفتنی

معادلات زیر را نمی‌توان با استفاده از قضیهٔ اصلی حل کرد:

${\displaystyle T(n)=2^{n}T\left({\frac {n}{2}}\right)+n^{n}}$

a مقدار ثابت نیست.

${\displaystyle T(n)=2T\left({\frac {n}{2}}\right)+{\frac {n}{\log n}}}$

اختلاف بین (f(n و ${\displaystyle n^{\log _{b}a}}$ غیر چندجمله‌ای است.

${\displaystyle T(n)=0.5T\left({\frac {n}{2}}\right)+n}$

a<۱ است درحالی که نمی‌توان کم تر از یک زیر مسئله داشت.

${\displaystyle T(n)=64T\left({\frac {n}{8}}\right)-n^{2}\log n}$:

(f(n مثبت نیست.

صحت قضیه اصلی

نشان دادن درست بودن این قضیه در حالت کلی کار ساده ای نیست اما در ادامه صحت این قضیه را برای یک حالت خاص بررسی می کنیم.

فرض می کنیم ^(f(n تابعی از مرتبه چندجمله ای باشد یعنی ^{(f(n) = Θ(nd} آنگاه :

${\displaystyle T(n)=aT\left({\frac {n}{b}}\right)+n^{d}}$

پس داریم :

log_b a > d −→ T(n) = Θ(n^logbb ^a)

log_b a = d −→ T(n) = Θ(n^{log a})

log_b a < d −→ T(n) = Θ(n^d)

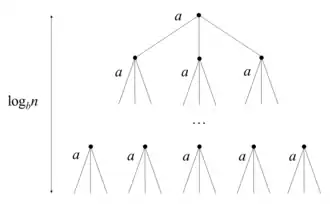
میخواهیم مجموع هزینه ها را به دست بیاوریم پس درخت بازگشت آن را رسم میکنیم. برای هر سطح در درخت هزینه های زیر را داریم :

هزینه ی رأسها در سطح ۱:${\displaystyle cn^{d}}$

هزینه ی رأسها در سطح ۲: ${\displaystyle ac\left({\frac {n}{b}}\right)^{d}}$

...

هزینه ی رأسها در سطحi :${\displaystyle a^{i-1}c\left({\frac {n}{b^{i-1}}}\right)^{d}}$

برای محاسبه هزینه کل ، هزینه های هر سطح را با هم جمع میزنیم.( تحلیل سرشکن )

مقدار رأس ریشه در درخت برابرn^d  است. به جز راسهای برگ ، هر رأس در این درختa  فرزند دارد که مقدار هرکدام_b )^-d ) برابر مقدار پدرش است؛ یعنی به عنوان مثال فرزندان ریشه مقداری برابر${\displaystyle \left({\frac {n}{b}}\right)^{d}}$  دارند. و هزینهی هر برگc است.  

با محاسبه جمع مقادیر سطوح مختلف درخت به مجموع کل میرسیم:

${\displaystyle T(n)\leq \sum _{i=0}^{\log {\left({\frac {n}{b}}\right)}-1}Ca^{i}\left({\frac {n}{b^{i}}}\right)^{d}+\theta (n^{\log _{b}a})}$

که این مقدار هزینهی متناظر با ریشه (T(n است را تعیین میکند.

قضیه اصلی برای تفریق و حل بازگشتی[1]

قضیه اصلی واکاوی الگوریتم‌ها برای تعیین کارکردهای دارای محدودیت بالایی Big - O استفاده می شود ، که می تواند در مسایل فرعی شکسته شود. قضیه اصلی برای تکرار تفریق و تقسیم: بگذارید T (n) تابعی باشد که مطابق شکل زیر در n مثبت نشان داده شده است:

قضیه اصلی برای تفریق و حل بازگشتی:

قضیه اصلی برای منها کردن

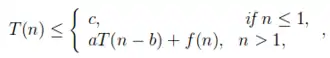
فرض کنید T (n) تابعی باشد که مطابق شکل در n مثبت نشان داده شده است:

1. If a<1 then T(n) = O(n^k)

2. If a=1 then T(n) = O(n^k+1)

3. if a>1 then T(n) = O(n^ka^n/b)

تحلیل زمانی چند الگوریتم

در حالت کلی روش مشخصی برای بهینه سازی الگوریتم ها وجود ندارد و بهینه سازی الگوریتم ، به خلاقیت نیازمنداست تا بتوان الگوریتمهای با مرتبه زمانی کمتر ارایه داد. با بررسی چند مثال روشهایی در این زمینه را معرفی میکنیم .

مساله حاصلضرب دو عدد

در ابتدا الگوریتم متداول برای حاصلضرب دو عدد را در نظر میگیریم. در این الگوریتم هر کدام ازn  درایه ازx  درn درایهy  ضرب می شود . واضح است که زمان اجرای این الگوریتم از مرتبهی ${\displaystyle \Theta (n^{2})}$ است .

همان طور که گفتیم در این بخش برای بهینه کردن مسأله ،الگوریتمهای دیگری معرفی کنیم. برای به دست آوردنحاصلضرب ، از روش تقسیم و حل استفاده میکنیم. مطابق زیر هر عددn  رقمی را به دو بخش _۲ⁿ رقمی تقسیم میکنیم:

${\displaystyle 10^{\left({\frac {n}{2}}\right)}\times a+b=x}$

${\displaystyle 10^{\left({\frac {n}{2}}\right)}\times c+d=y}$

حاصلضربx  وy  را میتوان به صورت زیر بازنویسی کرد:

${\displaystyle x.y=10^{n}a.c+10^{\left({\frac {n}{2}}\right)}(a.d+c.b)+b.d}$

Algorithm 1 : Multiply

function Multiply(x,y) n ← size of x aL ← left half digits of x aR ← right half digits of x bL ← left half digits of y bR ← right half digits of y [if number of digits of x or y is odd then add a 0 in begining of it(x or y)]

p₁ ← Multiply(aL,bL) p₂ ← Multiply(aL,bR) p₃ ← Multiply(aR,bL) p₄ ← Multiply(aR,bR)

return 10^n p₁+ 10^(n/2)(p₂ + p₃) + p₄

میتوان ابتدا هر کدام از حاصلضربهای سمت راست تساوی بالا را به صورت بازگشتی میتوان انجام داد و سپس بااستفاده از نتایج به دست آمده حاصلضرب مورد نظر را به دست آورد.

حال اگر تغییر متغیرهای زیر را در نظر بگیرید:

(p_۱ = a · c , p_۲ = b · d , p_۳ = (a + b)(c + dحاصلضربx · y  را به صورت زیر میتوان بازنویسی کرد:

                                                             ${\displaystyle 10^{n}p_{1}+10^{\left({\frac {n}{2}}\right)}(p_{3}-p_{2}-p_{1})+p_{2}}$

با نوشتن معادله بازگشتی روشن میشود که این روش نسبت به روش قبل زمان اجرای کمتری دارد. در مرحلهی تقسیم مسأله به سه زیر مسأله، هر کدام به اندازهی (T(ⁿ_۲ تقسیم میکنیم و هزینهی مرحلهی ادغام (Θ(n است، پس معادلهبازگشتی آن به صورت زیر است:

                                                                             ${\displaystyle T(n)=3T\left({\frac {n}{2}}\right)+\theta (n)\Rightarrow T(n)=\theta (n^{\log(}3)_{2})}$

Algorithm 2 : Multiply

function Multiply(x,y) n ← size of x if n = 1 then return x.y aR ← right half digits of x aL ← left half digits of x bR ← right half digits of y bL ← left half digits of y [if number of digits of x or y is odd then add a 0 in begining of it(x or y)]

p1 ← Multiply(aL,bL) p2 ← Multiply(aR,bR) p3 ← Multiply(aL + bL,aR + bR)

[until this line is same as privious algorithm]

${\displaystyle 10^{n}p_{1}+10^{\left({\frac {n}{2}}\right)}(p_{3}-p_{2}-p_{1})+p_{2}}$ return 

مساله حاصلضرب دو ماتریس

اگر با الگوریتم متداول یک ماتریسn × n  مانندx  را در یک ماتریسn × n  مانندy  ضرب کنیم هزینه ضرب از مرتبه${\displaystyle \theta (n^{3})}$ است .

برای این کار به روش تقسیم، هر ماتریسn × n  را به چهار زیرماتریس به شکل زیر تقسیم میکنیم:

${\displaystyle X_{n\times n}={\begin{pmatrix}A&B\\C&D\end{pmatrix}},Y_{n\times n}={\begin{pmatrix}E&F\\G&H\end{pmatrix}}\Rightarrow XY_{n\times n}={\begin{bmatrix}AE+BG&AF+BH\\CE+DG&CF+DH\end{bmatrix}}}$

با استفاده از تغییر متغیرهای زیر میتوانیم الگوریتم را بازنویسی کنیم:

T(n) = ۸T(ⁿ_۲) + θ(n^۲) =⇒ T(n) = θ(n^۳)

الگوریتم حاصلضرب دو ماتریس به همان روش عادی یعنی استفاده از دو حلقه یfor را در نظر میگیریم و میدانیم که هزینه ی آن ${\displaystyle \theta (n^{3})}$است، اما این روش مرتبه را کاهش نمیدهد پس به دلیل آن که میخواهیم الگوریتم را بهینهترکنیم ، برای این کار از چند متغیر جدید استفاده میکنیم.

${\displaystyle p_{1}=A.(F-H),p_{2}=H.(A+B),p_{3}=E.(C+D),p_{4}=D.(G-E),p_{5}=(A+D)(E+H),p_{6}=(B-D)(G-H),p_{7}=(A-C)+(E+F)}$

${\displaystyle XY_{n\times n}={\begin{bmatrix}P_{4}+P_{5}-P_{2}+P_{6}&P_{1}+P_{2}\\P_{3}+P_{4}&P_{1}+P_{3}-P_{5}+P_{7}\end{bmatrix}}}$

معادله ی بازگشتی به صورت زیر میشود:

                                                     T(n) = ۷T(ⁿ) + Θ(n^۲)       ⇒      T(n) = Θ(n^log۷۲)

واضح است که جواب این معادله از مرتبه زمانی T(n) = ۷T(ⁿ) + Θ(n^۲)     است.

میخواهیم در یک آرایه مرتب ، عدد خاصی را بیابیم. اولین روش آن است که تمام آرایه را بپیماییم که از مرتبهn است. حال میخواهیم روشی را معرفی کنیم که بتواند با زمان کمتری این کار را انجام دهد.

جستوجوی دودویی

ورودی: آرایهی مرتب(A = ⟨a1,a2,...,an و کلیدkey

خروجی: اندیسi ، به طوری کهA[i] = key . درصورتی که هیچi ای یافت نشد 1− برگرداند.

میخواهیم در یک آرایه مرتب ، کلید خاصی را بیابیم. اولین روش آن است که تمام آرایه را بپیماییم که از مرتبهn است. در الگوریتمی که در ادامه توضیح داده شده است این کار را با مرتبه زمانی کمتری انجام می دهد. از روش تقسیم استفاده میکنیم یعنی آرایه را به دو قسمت تقسیم میکنیم و هرکدام را جداگانه در جستوجوی دودویی قرارمیدهیم تاجایی که به جواب برسیم.

Algorithm 3 : Recursive Binary Search

function RecursiveBinarySearch(A,key,low,high)

if high < low then

return else

if key < A[mid] then return RecursiveBinarySearch(A,key,low,mid − 1)

else if _{key > A[mid]} then return RecursiveBinarySearch(A,key,mid + 1,high)

return mid

در الگوریتم بعدی جستوجوی دودویی به صورت غیربازگشتی ارایه شده است.

Algorithm 4 : Binary Search

function BinarySearch(A,n,key)

low ← 1n highwhile←low ≤ high do

if key < A⌊ [mid] then⌋

high ← mid − 1 else if key > A[mid] then

low ← mid + 1

else return mid 

return −1

جستارهای وابسته

• علامت O بزرگ

منابع

1. Yash Singla (5/16/2020). "Master Theorem For Subtract and Conquer Recurrences". www.geeksforgeeks.org. Check date values in: |تاریخ= (help)

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7.
• Michael T. Goodrich and Roberto Tamassia. Algorithm Design: Foundation, Analysis, and Internet Examples. Wiley, 2002. ISBN 0-471-38365-1. The master theorem (including the version of Case 2 included here, which is stronger than the one from CLRS) is on pp. 268–270.
• مشارکت‌کنندگان ویکی‌پدیا. «Master theorem». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳ می ۲۰۱۱.