قطب و خط قطبی

در هندسه، قطب و خط قطبی (انگلیسی: Pole and polar‎) به‌ترتیب نقطه و خطی هستند که رابطهٔ بازگشتی یکتایی نسبت به یک مقطع مخروطی معین دارند.

خط قطبی q به نقطهٔ Q نسبت به دایره‌ای با شعال r و مرکز O. نقطهٔ P نقطهٔ معکوس Q است؛ خط قطبی از P می‌گذرد و بر خطی که از O, P و Q می‌گذرد عمود است.

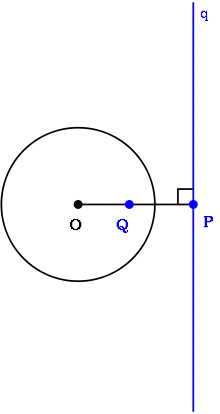
ویژگی‌ها

قطب و خط قطبی ویژگی‌های مفیدی دارند که برخی از آن‌ها عبارتند از:

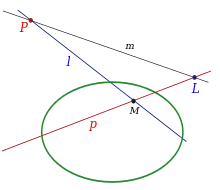
• اگر نقطهٔ P روی خط l باشد، قطب L متعلق به خط l روی خط قطبی p مرتبط با نقطهٔ P است.
• اگر نقطهٔ P در راستای خط l حرکت کند، خط قطبی‌اش (p) به دور قطب L خط l خواهد چرخید.
• اگر بتوان دو خط مماس از قطب به یک مقطع مخروطی رسم کرد، خط قطبی آن قطب هر دو را قطع می‌کند.
• اگر نقطه‌ای روی یک مقطع مخروطی باشد، خط قطبی آن مماسی است که از این نقطه به مقطع مخروطی می‌رود.
• اگر نقطه P روی خط قطبی خودش باشد، آنگاهP روی مقطع مخروطی است.
• هر خطی نسبت به یک مقطع مخروطی یک و فقط یک قطب دارد.

مقاطع مخروطی

خط p خط قطبی نقطه P است، همچنین l برای L و m برای M

کارل گئورگ کریستیان فان اشتات (۱۷۹۸ - ۱۸۶۷) نشان داد که رابطه‌ای که یک مقطع مخروطی بین قطب و خط قطبی ایجاد می‌کند از خود منحنی بنیادی‌تر است و می‌تواند برای تعریف این منحنی‌ها به شکلی متقارن و برگشتی (به عنوان مکان هندسی نقاطی که روی خط قطبی خودشانند، یا پوش (ریاضی) ‏(en)‏ خطوطی که از قطب خودشان می‌گذرند) به‌کار رود.[1]

اگر معادلهٔ بیضی را از معادلهٔ عام منحنی‌های درجهٔ دوم نوشته شود ${\displaystyle (A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0)}$، معادلهٔ خط قطبی نقطهٔ ${\displaystyle (\xi ,\eta )}$ عبارت خواهد بود از:[2]

${\displaystyle Dx+Ey+F=0}$

که در آن ${\displaystyle D}$ و ${\displaystyle E}$ و ${\displaystyle F}$ ثابت‌هایی‌اند که به شکل زیر تعریف می‌شوند:

${\displaystyle {\begin{aligned}D&=A_{xx}\xi +A_{xy}\eta +B_{x}\\E&=A_{xy}\xi +A_{yy}\eta +B_{y}\\F&=B_{x}\xi +B_{y}\eta +C\,\end{aligned}}}$

با داشتن معادلهٔ خط قطبی ${\displaystyle (Dx+Ey+F=0)}$ نیز می‌توان قطب آن را با قرار دادن مقادیر ${\displaystyle x}$ و ${\displaystyle y}$ و ${\displaystyle z}$ از محاسبهٔ زیر در ${\displaystyle \left({\frac {x}{z}},{\frac {y}{z}}\right)}$ بدست آورد:[3]

${\displaystyle {\displaystyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{bmatrix}}^{-1}\cdot {\begin{bmatrix}D\\E\\F\end{bmatrix}}}}$

جستارهای وابسته

• هندسه تصویری

منابع

1. Coolidge 1945‏:‎64-66
2. Coolidge 1945‏:‎64-66
3. Coolidge 1945‏:‎64-66

• مشارکت‌کنندگان ویکی‌پدیا. «Pole and polar». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۳۱ دسامبر ۲۰۱۸.

پیوند به بیرون

در ویکی‌انبار پرونده‌هایی دربارهٔ قطب و خط قطبی موجود است.