ماشین تعیین ناپذیر با ε حرکت

در نظریه اتوماتا، ماشین تعیین ناپذیر با ε حرکت[1](NFA-ε)، حالت توسعه یافته اتوماتون تعین‌ناپذیر متناهی (NFA) است، به طوری که بدون مصرف هیچ حرف ورودی، می‌تواند به حالت[2] جدیدی تبدیل شود. انتقال، بدون مصرف هیچ گونه نماد ورودی را ε-گذار[3]می‌نامند.

ε-گذار، یک راه حل مناسب، برای طراحی سیستم‌هایی را فراهم می‌کند که تا به حال، حالتهای[4]این سیستم‌ها دقیقاً شناخته نشده‌است.ε-گذار هیچ ظرفیت بیشتری برای تفهیم زبان صوری ندارد. NFA و NFA-ε هر دو برای تفهیم یک موضوع از زبان صوری هستند، موضوعی به نام زبان منظم.NFA-ε را تعریف می‌کنیم چون اثبات برخی خواص بر روی آن‌ها نسیت بهNFA آسان تر است. از آنجا که یک NFA-ε همیشه می‌تواند به NFA تبدیل شود پس تمام ویژگی‌ها نیز برای NFA صدق است.

تعریف غیر رسمی

به‌طور مثال فرض کنید NFA-ε شامل دو حالت ۱ و ۲ است و می‌تواند بدون مصرف هیچ نمادی از رشته ورودی به حالت۲ رود. اگر در حالت ۱ باشد، و نماد ورودی بعدی a باشد، ابهامی وجود دارد: آیا این سیستم قبل از استفاده از نماد a در حالت ۱ است یا حالت ۲؟به خاطر این ابهام، بهتر است از مجموعهٔ حالتهای ممکن بگوییم که ممکن است وارد سیستم بشود. بنابراین، قبل از مصرف نماد a، این ماشین می‌تواند در هر یک از حالتهای مجموعه {1و ۲} باشد. معادلاً می‌توان تصور کرد که NFA همزمان در حالت ۱و ۲ است و این اشاره غیر مستقیمی powerset construction دارد که معادل ترجمه NFA به DFA است.

تعریف رسمی

NFA-ε به یک پنج‌تائی گفته می‌شود، که شامل:

  • یک مجموعهٔ متناهی از حالات
  • یک مجموعهٔ متناهی از نمادهای ورودی موسوم به الفبا
  • حالت آغازین (q0 ∈ Q)
  • مجموعهٔ حالات نهائی یا مجموعهٔ حالات مورد قبول (F ⊆ Q)
  • تابع انتقال ((δ:Q × (Σ ∪{ε}) → P(Q)

است.

مثال
نمودار حالتها M

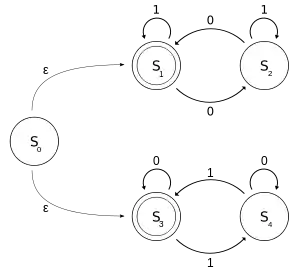
فزض کنیم M یک NFA-ε است با الفبا دودویی {0،1}، به طوریکه ورودی شامل تعداد زوج ۱ یا تعداد زوج ۰ است.

M = ({s0, s1, s2, s3, s4}, {0, 1}, Δ, s0, {s1, s3})

0
1
ε
S0
{}
{}
{S1, S3}
S1
{S2}
{S1}
{}
S2
{S1}
{S2}
{}
S3
{S3}
{S4}
{}
S4
{S4}
{S3}
{}

ویژگی‌های بستاری

اگر زبانِ NFA-ε حاصل از اعمال عملیاتی بر NFA-εها قبل، NFA-ε شناخته شده باشد، گفته می‌شود که NFA-εها تحت آن عملیات بسته هستند. NFA-εها تحت عملیات زیر بسته هستند:

منابع
  1. Nondeterministic finite automaton with ε-moves
  2. State
  3. ε-transition
  4. States
  5. union
  6. Intersection
  7. Concatenation

پیوند به بیرون
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.