مختصات یاکوبی

در تئوری سیستم های ذره ای ، مختصات یاکوبی اغلب برای ساده سازی فرمول ریاضی استفاده می شوند. این مختصات به ویژه در مولکولهای چند اتمی و واکنشهای شیمیایی ، [1] و در مکانیک سماوی رایج است. [2] یک الگو برای تولید مختصات یاکوبی برای بدن N ممکن است بر پایه درخت دودویی باشد. [3] در کلمات ، الگو به شرح زیر است: [3]

یاکوبی برای مسئله دو جسم هماهنگی می کند .${\displaystyle {\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1}+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}}$ و ${\displaystyle {\boldsymbol {r}}={\boldsymbol {x}}_{1}-{\boldsymbol {x}}_{2}}$ با ${\displaystyle M=m_{1}+m_{2}}$ . [4]

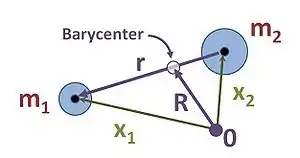
بگذارید m _j و m _k جرم دو بدن باشند که بدن جدیدی از جرم مجازی M = m _j + m _k جایگزین می شوند. مختصات موقعیت x _j و x _k با موقعیت نسبی آنها r _jk = x _j جایگزین می شوند   −   x _k و توسط بردار به مرکز جرم آنها R _jk = ( m _j q _j + m _k q _k ) / ( m _j + m _k ). گره موجود در درخت دودویی که مربوط به بدن مجازی است m _{j را} به عنوان فرزند راست خود و m _k به عنوان فرزند چپ خود قرار داده است. منظور از کودکان نشان دهنده نسبی مختصات نقاط از x _K به x _J. مرحله بالا را برای N تکرار کنید   −   ۱ بدن ، یعنی ن   −   ۲ بدن اصلی به همراه بدن مجازی جدید.

مجموعه احتمالی مختصات یاکوبی برای مشکل چهار بدن. مختصات یاکوبی r _۱ ، r _۲ ، r _۳ و مرکز جرم R است .[5]

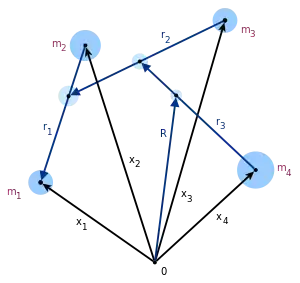
برای مشکل بدن - ان نتیجه این است: [6]

${\displaystyle {\boldsymbol {r_{j}}}={\frac {1}{m_{0j}}}\sum _{k=1}^{j}m_{k}{\boldsymbol {x_{k}}}\ -\ {\boldsymbol {x_{j+1}}}\,\quad (j=1,2,\dots ,N-1)}$

${\displaystyle {\boldsymbol {r_{N}}}={\frac {1}{m_{0N}}}\sum _{k=1}^{N}m_{k}{\boldsymbol {x_{k}}}\,}$

با

${\displaystyle m_{0j}=\sum _{k=1}^{j}\ m_{k}\ .}$

بردار ${\displaystyle {\boldsymbol {r_{N}}}}$ مرکز جرم بدن است:

نتیجه ای که با آن باقی مانده است ، بنابراین یک سیستم از مختصات N -۱ به طور ترجمه ای بی تحرک است ${\displaystyle {\boldsymbol {r_{1}}},\dots ,{\boldsymbol {r_{N-1}}}}$ و یک مرکز هماهنگی جمعی ${\displaystyle {\boldsymbol {r_{N}}}}$ ، از تکرار سیستمهای دو بدن در سیستم چند بدن.

منابع

1. John Z. H. Zhang (1999). Theory and application of quantum molecular dynamics. World Scientific. p. 104. ISBN 981-02-3388-4.
2. For example, see Edward Belbruno (2004). Capture Dynamics and Chaotic Motions in Celestial Mechanics. Princeton University Press. p. 9. ISBN 0-691-09480-2.
3. Hildeberto Cabral, Florin Diacu (2002). "Appendix A: Canonical transformations to Jacobi coordinates". Classical and celestial mechanics. Princeton University Press. p. 230. ISBN 0-691-05022-8.
4. David Betounes (2001). Differential Equations. Springer. p. 58; Figure 2.15. ISBN 0-387-95140-7.
5. Patrick Cornille (2003). "Partition of forces using Jacobi coordinates". Advanced electromagnetism and vacuum physics. World Scientific. p. 102. ISBN 981-238-367-0.
6. Patrick Cornille (2003). "Partition of forces using Jacobi coordinates". Advanced electromagnetism and vacuum physics. World Scientific. p. 102. ISBN 981-238-367-0.