مرکز جرم

مرکز جِرم (به انگلیسی: Center of mass) یک دستگاه از ذرات، در فیزیک، نقطهٔ مشخصی است که در بسیاری از مسائل سیستم طوری رفتار می‌کند که گویی همهٔ جرم آن در آن نقطه متمرکز است. مرکز جرم فقط تابعی از جای و جرم ذراتی است که سامانهٔ صلب را تشکیل می‌دهند.

این اسباب‌بازی با استفاده از اصول مرکز ثقل برای حفظ تعادل آن بر سر یک انگشت طراحی و ساخته شده‌است

در صورتی که ذرات سیستم تا حدودی آزادانه در کنار هم باشند، مانند مجموعه ساچمه‌هایی که از تفنگ ساچمه‌ای شلیک شده، مرکز جرم نقطه‌ای در فضا و بین گلوله‌ها است که ممکن است روی هیچ‌کدام از آن گلوله‌ها واقع نباشد. مرکز جرم یک جسم همیشه روی مرکز هندسی آن نیست؛ و نقطهٔ دیگری می‌تواند مرکز جرم جسم باشد.

تعریف

مرکز جرم یک سیستم از ذرات میانگین وزن‌دار مکان‌های آن ذرات است.
سیستم کلی ما شامل n ذره به جرم‌های ${\displaystyle m_{1},m_{2},...,m_{n}}$ است که بردار مکان آنها، به ترتیب عبارتند از ${\displaystyle {\overrightarrow {r_{1}}},{\overrightarrow {r_{2}}},...,{\overrightarrow {r_{n}}}}$ . مرکز جرم این سیستم نقطه‌ای است به بردار مکان ${\displaystyle {\overrightarrow {r_{cm}}}}$ که از رابطهٔ زیر به دست می‌آید:

${\displaystyle {\overrightarrow {r}}_{cm}={\dfrac {m_{1}{\overrightarrow {r_{1}}}+m_{2}{\overrightarrow {r_{2}}}+...+m_{n}{\overrightarrow {r_{n}}}}{m_{1}+m_{2}+...+m_{n}}}={\dfrac {\sum _{i}m_{i}{\overrightarrow {r_{i}}}}{m}}}$

در اینجا m جرم کلی سیستم است. بدیهی است که تعریف بالا با سه معادلهٔ زیر برابر است:

${\displaystyle {\overrightarrow {x}}_{cm}={\dfrac {\sum _{i}m_{i}{\overrightarrow {x_{i}}}}{m}},{\overrightarrow {y}}_{cm}={\dfrac {\sum _{i}m_{i}{\overrightarrow {y_{i}}}}{m}},{\overrightarrow {z}}_{cm}={\dfrac {\sum _{i}m_{i}{\overrightarrow {z_{i}}}}{m}}}$

که y، x و z مقادیر گرانیگاه را در فضا مشخص خواهند کرد.[1]

مثال‌ها

• مرکز جرم یک دستگاه دوذره‌ای روی خط و اصل آن دو ذره قرار دارد. (یا دقیق‌تر مرکز جرم‌های فردی آن‌ها) مرکز جرم نزدیک‌تر است به جسم سنگین‌تر.
• مرکز جرم یک حلقه در مرکز آن حلقه‌است. (در فضا)
• مرکز جرم یک هرم روی امتداد هر سه میانه قرار می‌گیرد. و بنابراین روی مرکز ثقل -که همچنین میانگین سه راس است- قرار می‌گیرد.
• مرکز جرم یک مستطیل روی تقاطع دو قطر است.
• در یک جسم کروی منظم، مرکز جرم در مرکز قرار دارد. این تقریباً شامل کرهٔ زمین هم می‌شود؛ با اینکه غلظت به‌طور قابل توجهی تغییر می‌کند. ولی عمدتاً و تا حد کمی به مختصات دیگر بستگی دارد.
• به‌طور کلی برای هر قرینه از یک جسم، مرکز جرم آن، یک نقطهٔ ثابت خواهد بود از آن قرینه.

تاریخچه

مفهوم مرکز ثقل اولین بار توسط ارشمیدس مطرح شد. ارشمیدس نشان داد که نیروی پیچشی (گشتاور) اعمال شده روی یک اهرم به وسیله قرار دادن وزنه‌ها روی نقاط گوناگون در امتداد اهرم همان نیرویی است که به اهرم وارد می‌شد اگر تمام وزنه‌ها روی یک نقطه قرار می‌گرفت-مرکز ثقل آنها-. در مورد حرکت اجسام شناور روی آب او نشان داد که جهت جسم شناور جهتی است که مرکز ثقل جسم را کمتر می‌کند. (مرکز ثقل جسم در آن جهت کمتر است.) او تکنیک‌های ریاضی را بسط داد برای پیدا کردن مراکز ثقل اجسام دارای چگالی یکنواخت_ اشکال_خوش تعریف. به ویژه یک مثلث و یک نیمکره و یک مخروط یا هرم _ناقص_یک قطع مخروطی دایروی.

در قرون وسطی تئوری‌های راجع به مرکز ثقل بیشتر توسعه داده شد توسط ابوریحان بیرونی، عبدالرحمن صوفی، عمر خیام و خزینی.

حرکت

معادلات حرکت زیر بر پایهٔ این فرض بنا شده‌اند که یک سیستم از ذرات وجود دارد که به وسیلهٔ نیروهای داخلی و خارجی کنترل شده‌است. یک نیروی داخلی نیرویی است که به وسیلهٔ فعل و انفعالات ذرات داخل سیستم ایجاد شده‌است. و یک نیروی خارجی نیرویی است که از خارج از سیستم سرچشمه می‌گیرد و عمل می‌کند روی یک یا چند ذره داخل سیستم. نیروی خارجی لازم نیست حتماً ناشی از یک جسم یکنواخت باشد. برای هر سیستمی که هیچ نیروی خارجی به آن وارد نمی‌شود، گرانیگاه با سرعت ثابت حرکت می‌کند. این قانون برای همهٔ سیستم‌ها با نیروهای داخلی کلاسیک شامل میدان‌های مغناطیسی، میدان‌های الکتریکی، واکنش‌های شیمیایی و غیره به کار برده می‌شود. به عبارت دیگر این قانون درست است برای هر نیروی داخلی که صورت ضعیف قانون سوم نیوتون در آن صدق می‌کند. نیروی حرکت آنی مجموع برای هر سیستم از ذرات به وسیلهٔ فرمول زیر داده شده‌است:

P=MVcm

جاییکه M نماد جرم کل وVcm سرعت گرانیگاه باشد. این سرعت می‌تواند محاسبه شود به وسیلهٔ اندازه‌گیری زمان گرفته شده از مکان گرانیگاه. یک فرمول شبیه به قانون دوم نیوتون هست: F=Macm وقتی F نماد مجموع تمام نیروهای خارجی باشد و acm نمادی باشد برای شتاب گرانیگاه.

گرانیگاه

مَرکَز ثِقْل (به انگلیسی: Center of gravity) یا گِرانیگاه[2] یک جسم، نقطه‌ای است که گشتاور ناشی از میدان گرانشی، حول آن نقطه صفر می‌شود. در شرایطی که میدان گرانشی یکنواخت باشد، مرکز ثقل با مرکز جرم یکسان خواهد بود، اما در حالت کلی و در میدان‌های غیریکنواخت، مرکز جرم می‌تواند از گرانی‌گاه منحرف شود. برای مثال، برای یک ماهواره در مدار زمین، گرادیان میدان گرانشی بین دو قسمت دورتر و نزدیک‌تر ماهواره به زمین، می‌تواند یک گشتاور روی ماهواره ایجاد کند. در چنین شرایطی توجه یه تفاوت مرکز جرم و مرکز ثقل الزامی است.

این موضوع حداقل از دو طریق قابل مشاهده‌است:

• انرژی پتانسیل گرانشی یک سیستم برابر است با انرژی پتانسیل یک ذرهٔ نقطه‌ای دارای جرم کل M، که در R قرار دارد.
• گشتاور گرانشی روی یک سیستم برابر است با یک گشتاور نیروی Mg که در R عمل می‌کند.

R × Mg = ∑ mi ri × g

خلاصه

در مورد مرکز جرم (center of mass) که آن را با c.m نشان می‌دهیم، برای دستگاه ذرات زیر داریم:

${\displaystyle \sum _{k=1}^{3}{\overrightarrow {r_{k}}}m_{k}={\overrightarrow {0}}}$

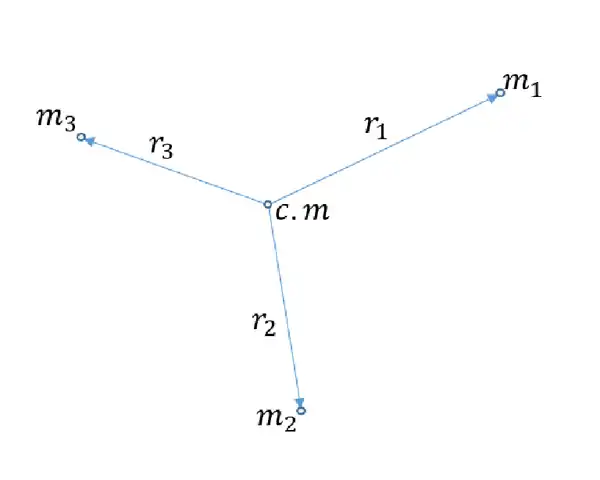
که در حالت کلی برای یک جسم صلب به صورت زیر در می آید:

${\displaystyle \int {\overrightarrow {r}}\operatorname {d} \!m={\overrightarrow {0}}}$

اما در مورد مرکز ثقل یا گرانیگاه (center of gravity) که آن را با G نمایش می‌دهیم، برای دستگاه ذرات زیر داریم:

${\displaystyle \sum _{k=1}^{3}{\overrightarrow {r_{k}}}\times {\overrightarrow {w_{k}}}={\overrightarrow {0}}}$

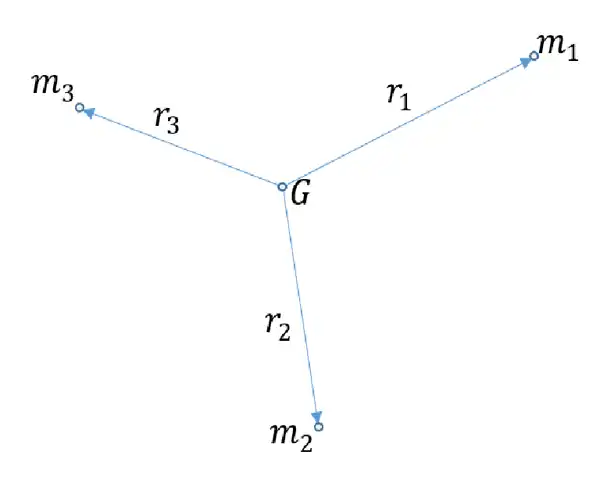
که در حالت کلی برای یک جسم صلب به صورت زیر در می آید:

${\displaystyle \int {\overrightarrow {r}}\times {\overrightarrow {\operatorname {d} \!w}}={\overrightarrow {0}}}$

منابع

1. مکانیک تحلیلی, گرانت فولز و جورج کسیدی, ترجمه جعفر قیصری, مرکز نشر دانشگاهی
2. «گرانیگاه» [ژئوفیزیک، علوم جَوّ] هم‌ارزِ «centre of gravity»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر اول. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۳۱-۱ (ذیل سرواژهٔ گرانیگاه)