ارشمیدس

اَرشِمیدُس (به یونانی: Άρχιμήδης) (زادهٔ ۲۸۷ ق. م – ۲۱۲ ق. م^∗) همه‌چیزدان ،فیلسوف، ریاضی‌دان، فیزیک‌دان، مهندس، مخترع و اخترشناس یونان باستان و از اهالی جزیرهٔ ساموس در دریای مدیترانه بود.

ارشمیدس
ارشمیدس، تابلویی اثر دومنیکو فتی، ۱۶۲۰ در موزه آلته‌مایستر، درسدن آلمان
نام بومی	Ἀρχιμήδης
زادهٔ	۲۸۷ پیش‌از میلاد سیراکوز
درگذشت	c. ۲۱۲ پیش‌از میلاد (سن حدود ۷۵) سیراکوز
محل زندگی	سیراکوز
شناخته‌شده برای	اصل ارشمیدس پیچ ارشمیدس استاتیک شاره‌ها اهرم‌ها
پیشینه علمی
رشته(های) فعالیت	ریاضیات، فیزیک مهندسی، اخترشناسی

زندگی‌نامه

ارشمیدس دانشمند و ریاضیدان یونانی در سال ۲۷۸ قبل از میلاد در شهر سیراکوز یونان زاده شد و در جوانی برای آموختن دانش به اسکندریه رفت. بیشتر دوران زندگیش را در زادگاهش گذراند و با فرمانروای این شهر دوستی نزدیک داشت. زندگی ارشمیدس با آرامش کامل می‌گذشت. زمانی که رومیان در سال ۲۱۲ قبل از میلاد شهر سیراکوز را به تصرف خود درآوردند سردار رومی مارسلوس دستور داد که هیچ‌یک از سپاهیانش حق اذیت و آزار و توهین و ضرب و جرح ارشمیدس را ندارند،[1] با این حال ارشمیدس قربانی غلبهٔ رومیان بر شهر سیراکوز شد و به دست یک سرباز مست رومی در ۲۱۲ قبل از میلاد کشته شد و این در حالی بود که در میدان بازار شهر در حال اندیشیدن به مسئله‌ای ریاضی بود. می‌گویند آخرین سخن او این بود: دایره‌هایم را خراب نکن.

کشف بزرگ ارشمیدس (اورکا اورکا)

چنین گفته شده‌است که هیرو (هایرُن) پادشاه سیراکوز زرگری را مأمور کرده بود تا برایش تاجی از طلای ناب بسازد. وقتی تاج تکمیل شد و به دست پادشاه رسید، وی تردید داشت که زرگر تمام طلا را به کار برده باشد. شاه هیرو دوست خود ارشمیدس را احضار کرد و از او خواست تا بفهمد آیا واقعاً تاج از طلای ناب است یا نه؟ در سدهٔ سوم پیش از میلاد، شیمی تحلیلی به اندازهٔ ریاضیات پیشرفته نبود و ارشمیدس در ریاضیات و مهندسی توانایی بسیار داشت. ارشمیدس قبلاً برای محاسبهٔ حجم جامدهایی که شکلی منظم مثل کُره یا استوانه داشتند دستورهای ریاضی ابداع کرده بود. او می‌دانست که اگر بتواند حجم تاج هیرو را تعیین کند خواهد فهمید که آیا تاج از طلای ناب درست شده‌است یا از مخلوطی از طلا با فلزات دیگر ساخته شده‌است. وقتی پا به خزینه گذاشت و دید که آب از آن سرریز کرد فهمید که حجم آبی که بیرون ریخته‌است دقیقاً با حجم قسمتی از بدن او که وارد آب شده برابری می‌کند، بنابراین دریافت که اگر تاج را در ظرف آبی قرار دهد حجم آبی که از ظرف سرریز می‌شود یا در آن بالا می‌رود حجم تاج است. وی که بسیار هیجان‌زده شده بود برهنه از حمام بیرون دوید و فریاد زد یافتم! یافتم! (اورکا اورکا). او در آزمایش خود تشخیص داد که تاج شاهی میزان بیشتری آب را نسبت به شمش طلای هم‌وزنش پس می‌راند، ولی این میزان آب کمتر از میزان آبی است که شمش نقرهٔ هم‌وزن آن را جابه‌جا می‌کند. به این ترتیب ثابت شد که تاج شاهی از طلای ناب ساخته نشده و زرگر آن را از مخلوطی از طلا و نقره ساخته‌است و این‌گونه ارشمیدس یکی از رازهای طبیعت را کشف کرد، یعنی این که می‌توان حجم اجسام با شکل نامنظم را با کمک مقدار مایعی که جابه‌جا می‌کنند اندازه‌گیری کرد.

اگر چه به نظر می‌رسد این داستان همچون بسیاری از کشفیات علمی (مثل داستان نیوتن و درخت سیب) دچار غلو و انحراف شده باشد ولی شهرتی جهانگیر دارد و کمابیش در همهٔ جهان شناخته شده‌است. روایت دیگری که به نظر می‌رسد از وجاهت بیشتری برخوردار باشد مربوط می‌شود به فرمان ساخت کشتی غول‌آسایی به نام «سیراکوسیا» از سوی پادشاه هایرون که منجر به کشف قانون شناوری یا همان اصل ارشمیدس شد.[2]

پیچ ارشمیدس

مقاله اصلی: پیچ ارشمیدس

نمای سه‌بُعدی پیچ ارشمیدس

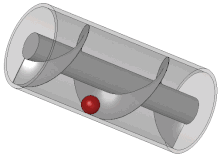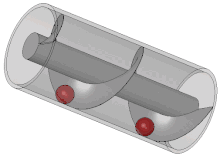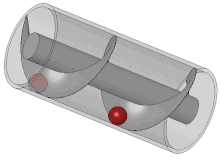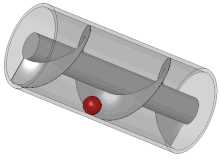
اختراعی منسوب به ارشمیدس که در گذشته از آن برای آبیاری و بالا کشیدن آب‌های زیرزمینی استفاده می‌کردند. به شکل لوله‌ای مارپیچ بود که محور آن زاویه‌ای ۴۵ درجه با راستای افقی می‌ساخت. یک سر پیچ در مخزن آب قرار داشت، با چرخاندن پیچ آب از لوله بالا می‌رفت. برخی از محققان معتقدند که نوع دیگری از این پیچ برای آبیاری باغ‌های معلق بابل استفاده می‌شده‌است. او مخترع پمپ انتقال مایعات است که پیچ ارشمیدس نام دارد. می‌گویند او پس از کشف پیچ ارشمیدس تا ساعت‌ها از خوشحالی دور میدانی می‌دوید.

فعالیت در حوزه‌های دیگر

ارشمیدس در ریاضیات از ظرفیت‌های هوشی بسیار برخوردار بود. او منجنیق‌ هایی برای دفاع از سرزمین خود اختراع کرد که بسیار سودمند افتادند. او توانست سطح و حجم جسم‌هایی مانند کره، استوانه و مخروط را حساب کند و روش نوینی برای اندازه‌گیری در دانش ریاضی پدیدآورد. همچنین به دست آوردن عدد پی نیز از کارهای گران‌قدر وی است. او کتاب‌هایی دربارهٔ خصوصیات و روش‌های اندازه‌گیری اشکال و حجم‌های هندسی از قبیل مخروط، منحنی حلزونی و خط مارپیچ، سهمی، سطح کره و استوانه نوشته، علاوه بر آن او قوانینی دربارهٔ سطح شیب‌دار، پیچ، اهرم و مرکز ثقل کشف کرد.

یکی از روش‌های نوین ارشمیدس در ریاضیات به دست آوردن عدد پی بود. وی برای محاسبۀ عدد پی، یعنی نسبت محیط دایره به قطر آن روشی به دست داد و ثابت کرد که عدد محصور مابین ۷/۱ ۳ و ۷۱/۱۰ ۳ است. گذشته از آن روش‌های گوناگونی برای تعیین جذر تقریبی اعداد به دست داد و از مطالعه آن‌ها معلوم می‌شود که وی قبل از ریاضیدانان هندی با کسرهای متصل یا مداوم متناوب آشنایی داشته‌است. در حساب روش غیرعملی و چند عملی یونانیان را که برای نمایش اعداد از علائم متفاوت استفاده می‌کردند به کنار گذاشت و پیش خود دستگاه شمارشی اختراع کرد که به کمک آن ممکن بود هر عدد بزرگی را بنویسیم و بخوانیم.

دانش تعادل مایعات به‌وسیلۀ ارشمیدس کشف شد و وی توانست قوانین آن را برای تعیین وضع تعادل اجسام غوطه‌ور به کار ببرد. همچنین برای اولین بار برخی از اصول مکانیک را به وضوح و دقت بیان کرد و قوانین اهرم را کشف کرد.

بزرگترین افتخار ارشمیدس این بود که نسبت بین یک کره و استوانه محیط آن را بدست آورده‌است. کره ۲/۳ حجم استوانه را داراست و همین‌طور مساحت سطح کره ۲/۳ مساحت سطح استوانه است. بنابر وصیتش یک کره و یک استوانه بر روی مزارش حک شد.[3]

ارشمیدس و دیگر دانشمندان دوران خود

ارشمیدس دربارهٔ خود گفته‌ای دارد که با وجود گذشت قرن‌ها جاودان مانده: «نقطهٔ اتکایی به من بدهید تا زمین را از جا بلند کنم». مشابه همین گفته به صورت دیگری در متون ادبی زبان یونانی از قول ارشمیدس نقل شده‌است، اما مفهوم در هر دو صورت یکی است. ارشمیدس گوشه‌گیر و منزوی بود. در جوانی به مصر مسافرت کرد و مدتی در شهر اسکندریه به تحصیل پرداخت و در این شهر دو دوست قدیمی یافت، یکی از آن‌ها کونون است که ریاضیدان قابلی بود و ارشمیدس چه از لحاظ فکری و چه از نظر شخصیتی برای وی احترام قائل بود و دیگری اراتوستن که گرچه ریاضیدان لایقی بود، اما مردی سطحی به‌شمار می‌رفت که برای خویش احترام خارق‌العاده‌ای قائل بود.

ارشمیدس با کونون ارتباط و مکاتبه دائمی داشت و بخش مهمی از آثار خویش را در این نامه‌ها با او در میان گذاشت و بعد از مرگ وی، ارشمیدس با دوستی که از شاگردان کونون بود مکاتبه می‌کرد. در سال ۱۹۰۶ ج. ل. هایبرگ مورخ دانشمند و متخصص تاریخ ریاضیات یونانی در شهر قسطنطنیه موفق به کشف مدرک باارزشی شد. این مدرک کتابی است به نام قضایای مکانیک و روش آن‌ها که ارشمیدس برای دوست خود اراتوستن فرستاده بود. موضوع این کتاب مقایسه حجم یا سطح نامعلوم شکلی با حجم‌ها و سطوح معلوم اَشکال دیگر است که به‌وسیله آن ارشمیدس موفق به تعیین نتیجه مطلوب می‌شد.

از نکات علمی ارشمیدس روش‌های محاسبه اوست. وی دو هزار سال قبل از اسحاق نیوتن و لایب‌نیتس موفق به اختراع حساب انتگرال شد و حتی در حل یکی از مسائل خویش نکته‌ای به کار برد که می‌توان او را از پیش‌گامان فکر ایجاد حساب دیفرانسیل دانست.

بزرگترین فعالیت‌های علمی

• تعیین عدد پی
• ساخت قرقره ارشمیدس
• قانون چگالی در مایعات[4]

پانویس

• ^  "Archimedes of Syracuse". University of St Andrews. Retrieved ۲۴-۰۶-۲۰۰۷. Check date values in: |تاریخ بازدید= (help)

1. «عنوان مطلب». دانشنامه رشد. دریافت‌شده در ۲۱ فوریه ۲۰۲۰.
2. D'Angour, Armand, The real story behind Archimedes' Eureka!, retrieved 2019-04-03
3. مشارکت‌کنندگان ویکی‌پدیا (3 آپریل 2018). "Archimedes". Check date values in: |تاریخ= (help)
4. کتاب دانشمندان بزرگ انتشارات قدیانی فصل دوم

پیوند به بیرون

• آثار ارشمیدس در پروژهٔ گوتنبرگ

در ویکی‌انبار پرونده‌هایی دربارهٔ ارشمیدس موجود است.

مجموعه‌ای از گفتاوردهای مربوط به ارشمیدس در ویکی‌گفتاورد موجود است.