تثلیث زاویه
تثلیث زاویه به همراه تربیع دایره، تضعیف مکعب و چندضلعیهای منتظم محاط در دایره از مسائل سهگانه عهد باستان است که عدم امکان حلشدن آن در حالت کلی اثبات شدهاست. بزرگان ریاضی در طی دوران به راحتی میتوانستند با کشیدن نیمساز، هر زاویه دلخواه را به دو بخش برابر قسمت کنند، ولی در سه قسمت کردن کمان عاجز بودند؛ بنابراین تثلیث یا سه بخش کردن زاویه یکی از مسائل عهد باستان گردید.
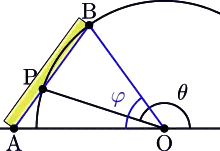
می توان با بهره گیری از قضایای مثلثات ثابت کرد که این مسئله (که جزء مسئلههای طرح شده در شاخه ساختمانهای هندسی است) در حالت کلی با کمک پرگار و سَتّاره (خطکش غیر مدرج) قابل حل نیست. با این حال، با حل معادله درجه ۳ زیر میتوان نشان داد که زاویه های بی شماری وجود دارند که با کمک خط کش غیر مدرج و پرگار قابل تثلیث هستند (از جمله زاویههای ۹۰ درجه یا ۴۵ درجه)، و همین طور، زاویه های بی شماری وجود دارند که به طریق مذکور قابل تثلیث نیستند (از جمله زاویهٔ ۶۰ درجه).
امکان حل این مسئله
در سال ۱۸۳۷، پیر ونزل مقالهای منتشر کرد و اثبات کرد که این مسئله در حالت کلی غیرقابل حل است.[1] در طول تاریخ بسیاری از ریاضیدانان برای حل این مسئله تلاش کردهاند و نام بسیاری از آنها و روشهای ارائه شده در کتابی گردآوری شدهاست.[2]
اگرچه حل مسئله در حالت کلی امکان ندارد، تثلیث برخی از زوایا امکانپذیر است. قضیهٔ زیر تمام زوایایی که میتوان تثلیث کرد را مشخص میکند:
قضیه: زاویهٔ میتواند تثلیث شود اگر و تنها اگر چندجملهای بر روی توسیع میدان تحویلپذیر (قابل حل) باشد.
در این قضیه Q نماد مجموعهٔ اعداد گویا است. اثبات این قضیه براساس تعمیم عدم امکان تثلیث زاویهٔ ۶۰ درجه سرراست است.[3]
ایرانیان پیش گام در رابطه با تثلیث زاویه
دانشمندان و ایرانیان بسیاری در راستای حل این مسئله پیشگام بودند که از جمله آنان میتوان به ابوعلی سینا و ابوریحان بیرونی اشاره کرد. در حال حاضرجواب قانع کنندهای برای این مسئله توسط آکادمی بینالمللی ریاضی تائید نشده است و عدم امکان حل آن برای حالت کلی اثبات شدهاست.
منابع
- Wantzel, Pierre-Laurent. "Recherches sur les moyens de reconnaître si un problème de géométrie peut se résoudre avec la règle et le compas." Journal de Mathématiques pures et appliquées 2.1 (1837): 366-372.
- Dudley, U.; America, Mathematical Association of (1994). The Trisectors. MAA spectrum. Mathematical Association of America. ISBN 978-0-88385-514-0. Retrieved 2014-09-18.
- Stewart, I. (2003). Galois Theory, Third Edition. Chapman Hall/CRC Mathematics Series. Taylor & Francis. p. 85. ISBN 978-1-58488-393-7. Retrieved 2014-09-19.
مطالعه بیشتر
نظری ساختمانهای هندسی، اوت آدلر، ترجمه پرویز شهریاری، انتشارات فردوس چاپ اول ۱۳۶۸، صفحات ۲۷۹ تا ۲۹۰
کتاب: آشنایی با تاریخ ریاضیات [هاوردو. ایوز] ترجمه محمد قاسم وحیدی اصل