مسئله درخت اشتاینر
مسئله درخت اشتاینر، که به افتخار یاکوب اشتاینر مبدع آن نام گذاری شده، کوچکترین درخت وزن داری است که شامل تعدادی از گرههای خاص به نام ترمینال باشد.
در این مسئله یک گراف وزن دار(G=(V،E و یک زیرمجموعه از رئوس گراف (T⊆V) که مجموعه ترمینالها نام دارد ارائه میگردد و هدف پیدا کردن('GT=(V'،E با کمترین هزینهاست که. E'⊆Eو T⊆V'⊆V
مسئله درخت اشتاینر دارای کاربردهای فراوانی نظیر مسیریابی یک به چند در شبکههای رایانهای، سامانههای ترابری، پلیس امداد، ایستگاههای پستی و کاربردهای دیگر میباشد.
مسئله درخت اشتاینر با مسئله درخت پوشای مینیمم مشابهت دارد: فرض کنید مجموعه رئوس V داده شدهاند، می خواهیم آنها را با یک گراف با کمترین وزن به هم متصل کنیم. به طوری که حاصل جمع وزنهای همه یالها کمینه شود. تفاوت بین مسئله درخت اشتاینر و مسئله درخت پوشای مینیمم این است که در مسئله درخت اشتاینر، رئوس میانه و یال ممکن است به گراف اضافه شوند تا وزن درخت پوشا را کاهش دهند. این رئوس جدید برای کاهش وزن کلی اتصالات معرفی میشوند و نقاط اشتاینر یا رئوس اشتاینر نام دارند. ثابت شدهاست که اتصالات به دست آمده یک درخت را تشکیل میدهند، که درخت اشتاینر نام دارد. ممکن است برای مجموعهای از رئوس درختهای اشتاینر زیادی وجود داشته باشند.
مسئله درخت اشتاینر در طراحی فیزیکی مدارات VLSI یا شبکه نیز کاربرد فراوانی دارد. بسیاری از نسخههای مسئله اشتاینر انپی کامل هستند.
درخت اشتاینر اقلیدسی
این مسئله انواع مختلفی دارد. دریک نوع آن تعدادی نقطه بر روی صفحه دو بعدی به عنوان ورودی ارائه میگردد و هدف، تولید درختی بر روی صفحه اقلیدسی است، که دارای کمترین هزینه بوده و همه نقاط را در بر بگیرد. همین مسئله به صورت عمود بر هم نیز مطرح میشود که در آن باید خطوط درخت فقط به صورت عمودی یا افقی رسم شوند که این مسئله در طراحی فیزیکی مدارات VLSI کاربرد فراوانی دارد.
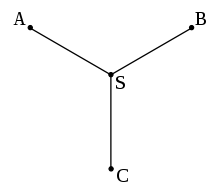
مشکل اصلی که ما با آن روبرو شدیم هندسه درخت اشتاینر بود: در طرح N نقطه داده شدهاست. هدف اتصال آنها به وسیله خطوطی است که کمترین وزن را داشته باشند.به طوری که هر دو نقطه یا به طور مستقیم (مسیری به طول یک) یا از طریق رئوس دیگر (مسیری به طول بیشتر از یک) به هم متصل هستند. این ممکن است به این صورت نشان داده شود که خطوط یکدیگر را قطع نمیکنند مگر در نقاط پایانی و درخت را تشکیل میدهند. برای مسئله اشتاینر اقلیدسی نقاطی که به گراف اضافه میشوند (نقاط اشتاینر) باید از درجه ۳ با شند. و سه لبهٔ متلاقی در یک نقطه باید با هم زاویه ۱۲۰ درجه را بسازند. این حد اکثر نقاط اشتاینر را به دنبال دارد که یک درخت اشتاینر میتواند حداکثر N-۲ نقطه اشتاینر داشته باشد، که N تعداد نقاط داده شدهاست. مسئله اشتاینر اقلیدسی یک انپی سخت است و بنابراین به عنوان جوابی بهینه برای الگوریتمهای محسوب نمیشود.
درخت اشتاینر متری
درختان اشتاینر در چهار چوب گراف وزندار مورد مطالعه قرار میگیرند. و آن را به صورت (G=(V،E،w نشان میدهیم. حال دو نوع مشکل وجود دارد: در مسئله بهینه سازی مربوط به درخت اشتاینر، هدف پیدا کردن کم وزنترین درخت اشتاینر است، در مسئله تصمیم گیری، ما مقدار k را در نظر میگیریم و هدف تعیین این است که آیا درخت اشتاینری از وزن کل حداکثر k وجود دارد.
ما میتوانیم توجه خود را به مورد خاصی که G گراف کامل باشد، محدود کنیم. هر راسی در فضای متریک محدود به یک نقطهاست و (w(e) برای هر یال e∈E متناظر با فاصله در فضا است. وزن یالها در نامساوی مثلث صدق میکند. این نوع به عنوان مسئله درخت اشتاینر متریک شناخته شدهاست. میتوان مثالی غیر متریک از مسئله درخت اشتاینر را در زمان از درجه پیچیدگی چندجملهای به عنوان مثال معادل مسئله درخت اشتاینر متریک تبدیل کرد؛ این تغییر ضریب تقریب را حفظ میکند.