مسئله سه روستا
مسئلهٔ سه روستا یا مسئلهٔ برق، آب، گاز (خدمات شهری) (به انگلیسی: Water, gas, and electricity) از رده معماهای ریاضی است.
فرض کنید که سه روستا در یک سطح (صفحه) یا یک کره قرار دارند و هر کدام مجبورند که به شرکتهای آب، برق و گاز وصل شوند. استفاده از سه بعد یا رفتن به درون روستاها یا شرکتها خلاف مقررات مسئلهاست. آیا راه حلی برای حل این مسئله بدون قطع کردن خطوط وجود دارد؟
تاریخچه
مبدأ مسئلهٔ ذیل بهعنوان مثالی از: «گراف دو قسمتی «» نامعلوم است اما میدانیم اولین بار در سال ۱۲۹۲ (۱۹۱۳ میلادی) توسط «هنری ارنست دودنی» (Henry Ernest Dudeney) بدینشکل مطرح شد: «مسئلهٔ گیجکننده عبارت است از: استقرار تجهیزات آب، گاز و برق بدون آنکه هیچ لوله یا خطی با دیگری تقاطع داشته باشد».
راه حل
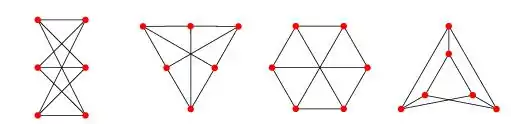
این مسئله بخشی از topological graph theory است که به مطالعه مباحث تعبیه گراف روی صفحات میپردازد. اگر بخواهیم کمی اصولی تر حرف بزنیم، این مسئله دربارهٔ اینکه آیا یگ گراف دو بخشی با ۶ راس ()مسطح است یا خیر. این گراف معادل با گراف دایرهای ( است.
Kazimierz Kuratowski در سال ۱۹۳۰ ثابت کرد که مسطح نیست و بنابراین این مسئله هیچ جوابی ندارد.این جواب میتواند شاهدی بر نتیجهٔ قضیه خم جردن Jordan curve theorem باشد. حکم کاملی که دربارهٔ گرافهای مسطحه در Kuratowski reduction theorem آمده شامل این نتیجه میشود.
حلقه شکل است یعنی در اینجا با سوراخ کردن صفحه (یا کره) میتوان مسئله را حل کرد، این ویژگیهای توپولوژیک مسئله را تغییر میدهد.
اثبات

یک اثبات ساده این مسئله به صورت زیر است:
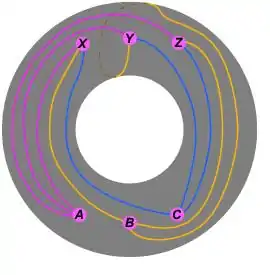
گرافی که از رئوس X-Y-Z-A-B-C تشکیل شدهاست را در نظر بگیرید.که در آن باید یال هایX-A,Y-B,Z-C باید حضور داشته باشند.حالا برای هر یال تصمیم میگیریم که ان را داخل یا خارج گراف دایرهای بکشیم. اما حتماً باید برای دو تا از یالها انتخاب یکسانی داشته باشیم. چون دو خط نمیتوانند در یک طرف بدون تقاطع کشیده شوند، گراف مسطح نیست.
کاربرد
هیچ فردی نمیتواند یک گراف که از دسته صفر نیست را در صفحه بدون تقاطع یالها بکشد. در طراحی مدارات الکتریکی وقتی که تمام مدارات به یک طرف برد محدود میشوند طراحی تمام مداراتی که شبیه به یک گراف غیر مسطح هستند غیرممکن میشود. تنها در مواردی که میتوان در سه بعد کار کرد یا از طرف دیگر برد استفاده کرد طراحی این مدارات امکانپذیر میباشد.
پیوند به بیرون
منابع
- Weisstein, Eric W. «Utility Graph.» From MathWorld—A Wolfram Web Resource.
- ریاضیات گسسته – ترجمه اردوان میرزائی
- ریاضیات گسسته - سیمور لیپ شوتز
- Chartrand, G. «The Three Houses and Three Utilities Problem: An Introduction to Planar Graphs.» §۹٫۱ in Introductory Graph Theory. New York: Dover, pp. ۱۹۱-۲۰۲، ۱۹۸۵.
- Coxeter, H. S. M. «Self-Dual Configurations and Regular Graphs.» Bull. Amer. Math. Soc. ۵۶، ۴۱۳-۴۵۵، ۱۹۵۰.
- Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. ۹۲-۹۴، ۱۹۸۴.
- Ore, Ø. Graphs and Their Uses. New York: Random House, pp. ۱۴-۱۷، ۱۹۶۳.
- Royle, G. «F۰۰۶A.» http://www.csse.uwa.edu.au/~gordon/foster/F006A.html%5Bپیوند+مرده%5D.
- Pappas, T. «Wood, Water, Grain Problem.» The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. ۱۷۵ and ۲۳۳، ۱۹۸۹.
- Steinhaus, H. Mathematical Snapshots, ۳rd ed. New York: Dover, pp. ۲۶۲-۲۶۳، ۱۹۹۹.