مسئله شام خوردن رمزنگاران
مسئله شام خوردن رمزنگاران (به انگلیسی: Dining Cryptographers Problem) مبحثیست که به چگونگی انجام محاسبات امن چند بخشی در توابع بولی میپردازد.
دیوید چام اولین فردی بود که در سال 1988 میلادی این بحث را ارائه و از این مسئله برای اثبات این موضوع که میتوان پیامی ناشناس را توسط هر گیرنده و فرستنده بدون محدودیت و غیرقابل رویت فرستاد، استفاده کرد. یعنی آنکه هویت فردی که یک پیام را میفرستد برای افرادی که پیام را دریافت مینمایند معلوم نگردد. یعنی هیچ دریافت کنندهای نمیتواند بفهمد که این پیام از جانب چه کسی ارسال گردیدهاست. این ناشناس بودن هویت فرد ارسالی در بسیاری از رمزنگاریها پیشرفته مورد استفاده قرار میگیرد. این پروتکل در واقع نیازمند تعامل بین چند سیستم میباشد تا بتوان از آن بهره برد و اگر بخواهیم از درستی این پروتکل مطمئن شویم تنها راه اینست که به درستی و صحت سیستمهای دیگر اطمینان داشته باشیم زیرا در غیر این صورت این پروتکل فاقد اعتبار خواهد بود.
مسئله شام خوردن رمزنگاران با وجود داشتن کلمات مشابه به مسئلهٔ شام خوردن فیلسوفان، هیچ ارتباطی ندارد و کاملاً از آن متمایز است(مسئله شام خوردن فیلسوفها در مبحث سیستم عامل و پردازشها بیان میشود).
شرح مسئله
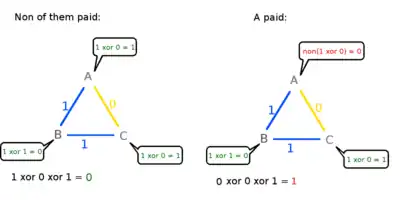
۳ رمزنگار برای صرف شام گرد یک میز جمع شدهاند. پس از صرف شام و هنگام پرداخت پول میز، پیشخدمت به آنها خبر میدهد که پول میز توسط یکی از رمزنگاران یا آژانس امنیت ملی پرداخت شدهاست. در نتیجه همهٔ آنها از این موضوع با خبر میشوند و به این کار که به طور ناشناس انجام شدهاست احترام میگذارند و از هویت فرد رمزنگار سؤال نمیپرسند تا هویت او گم نام باقی بماند؛ ولی میخواهند بدانند که آیا یکی از آنها پرداخت کننده پول میز بوده یا سازمان امنیت ملی این کار را انجام دادهاست. به خاطر همین آنها به تبادل پروتکل زیر اقدام مینمایند:
هر رمزنگار یک رقم ۰ یا ۱ را به دلخواه برای خود انتخاب میکند. سپس به طور خصوصی رقم انتخابی خود را به فرد سمت چپی خود اعلان میکند. هر رمزنگار رقم دریافتی را (رقمی را که از نفر سمت راستی خود دریافت کردهاست) با رقم انتخابی خود (رقمی که انتخاب کرده بود و به نفر سمت چپی خود فرستاده بود) فصل ضمنی (xor) میکند. اگر پرداخت کننده نباشد حاصل را به طور عمومی اعلان میکند. وگرنه مخالف باینری (not) حاصل را به طور عمومی اعلان میکند. سه رقمی که اعلان عمومی شدهاست با هم فصل ضمنی (xor) میشوند. اگر حاصل صفر باشد یعنی سازمان امنیت پرداخت کنندهاست و اگر ۱ باشد یعنی یکی از رمزنگاران پرداخت کنندهاست. اما به هر حال در این مسئله چنانچه یکی از رمزنگاران صورتحساب را پرداخت کرده باشد هویتش گم نام باقی میماند و رمزنگاران فقط میدانند که پول میز توسط سازمان امنیت ملی پرداخت نشدهاست.
محدودیتها
هرچند که این الگوریتم ساده و ظریف است اما محدودیتهایی نیز دارد:
- تصادم: هرگاه دو رمز نگار پول میز را پرداخت کرده باشند، پیام هریک پیام دیگری را خنثی مینماید و در نهایت نتیجه XOR آنها برابر با صفر میشود. این حالت را تصادم در مسئله مینامند که فقط در هر دوره تنها یک رمز نگار میتواند با این پروتکل به انتقال پیام خود بپردازد. به طور کلیتر هرگاه تعدادی زوج از رمزنگاران مبادرت به انتقال پیام خود نمایند این حالت به وقوع میپیوندد. در طرح پیشنهادی دیوید چام بیان میشود که بعد از تصادم یک بار دیگر پیام فرستاده شود اما در مقالهٔ او هیچ توضیح دقیقی دربارهٔ ترتیب ارسال پیام داده نشدهاست.
- رمزنگاری که در انتها بیت را دریافت میکند میتواند نتیجه را دستکاری کند. به عنوان مثال اگر رمزنگار انتهایی درستکار نباشد همواره میتواند پروتکل را نقض کند و نتیجه را صفر اعلام نماید؛ که این اتفاق به این سبب حادث میگردد که از فناوری کلید عمومی در این پروتکل استفاده نشدهاست. اما بدتر از آن موضوع این که پروتکل فاقد مکانیسمی برای تشخیص و اطمینان از پیروی کردن شرکت کنندگان از پروتکل است.
- پیچیدگی: این پروتکل نیازمند این است که کلید مخفی مشترکی بین هر دو شرکت کننده توزیع شود که اگر تعداد شرکت کنندگان زیاد باشد این خود به مسئلهای تبدیل میشود. هرچند که این پروتکل خاصیت امنیت بدون قید و شرط را داراست ولی زمانی تحقق مییابد که کانال بین آنها نیز همین گونه باشد که در عمل طراحی چنین کانال ارتباطی نا ممکن میباشد.
منابع
- مشارکتکنندگان ویکیپدیا. «Dining cryptographers problem». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۳ ژوئیه ۲۰۱۲.
برای مطالعه بیشتر
- Chaum, David (1988). "The Dining Cryptographers Problem: Unconditional Sender and Recipient Untraceability". Journal of Cryptology. ۱ (۱): ۶۵–۷۵. Retrieved July 13, 2012.
- Golle, P.; Juels, A. (2004). "Dining Cryptographers Revisited" (PDF). proc. of Eurocrypt: ۶۵–۷۵. Retrieved July 13, 2012.