ویلیام توماس تات

ویلیام توماس تات (به انگلیسی: William Thomas Tutte) (زاده ۱۴ مه ۱۹۱۷ - درگذشته ۲ مه ۲۰۰۲ ) ریاضی‌دان و رمزگشای اهل انگلستان است، که بعداً شهروند کانادا شد.

ویلیام توماس تات
زادهٔ	۱۴ مهٔ ۱۹۱۷ نیومارکت، سافولک، انگلستان
درگذشت	۲ مهٔ ۲۰۰۲ (۸۴ سال) کیچنر، انتاریو، کانادا
ملیت	انگلیسی-کانادایی
محل تحصیل	دانشگاه کمبریج
پیشینه علمی
رشته(های) فعالیت	ریاضیات
محل کار	دانشگاه تورنتو دانشگاه واترلو
استاد راهنما	شان وایلی

او دنباله‌ای از کدهای رمزنگاری آلمان را رمزگشایی کرد، و نقش بزرگی در موفقیت انگلیس در رمزگشایی‌های زمان جنگ داشت. او همچنین به نتایج اساسی در زمینه ترکیبیات، به خصوص در زمینه نظریه گراف، دست یافته‌است.

زندگی

کودکی

پدر ویلیام باغبان، و مادر او آشپز و خانه‌دار بود. خانواده آن‌ها بسته به اینکه پدرش در کجا کار کند تغییر جا می‌داد.

هنگامی که ۱۱ ساله بود، بورسیه تحصیلی برای مدرسه روزانه کمبریج دریافت کرد. در مدرسه از لحاظ تحصیلی بسیار درخشان ظاهر شد، ولی در این مقطع موضوعی که او را به خود علاقه‌مند کرده بود، ریاضی نبود، بلکه شیمی بود. او یک نسخه از کتاب «مقالات و سرگرمی‌های ریاضی» اثر روز بال را در کتابخانه مدرسه پیدا کرد، که در او علاقه‌ای نسبت به مسئله‌های نظریه گراف ایجاد کرد؛ ولی برای اینکه او رشته شیمی را برای تحصیل در دانشگاه انتخاب نکند کافی نبود.

دانشگاه

در سال ۱۹۳۵، تات برای تحصیل به ترینیتی کالج کمبریج رفت تا به تحصیل علوم طبیعی با تخصص شیمی بپردازد. پس از اینکه وارد ترینیتی کالج شد، علاقه او نسبت به ریاضی به آن درجه رسیده بود که به جامعه ریاضی ترینیتی بپیوندد، و پس از مدتی رابطه دوستی با تعدادی از ریاضی‌دان‌ها بنا نهاد. او با مدرکی در شیمی فارغ‌التحصیل شد و مشغول به تحقیق شد، و اولین دو مقاله خود در زمینه شیمی را در سال ۱۹۳۹ منتشر کرد. مقاله بعدی او همراه با سه نفر از دوستانش در زمینه ارتباط تجزیه مستطیل به مربع‌ها با نظریه گراف‌ها در سال ۱۹۴۰ منتشر شد.

جنگ جهانی دوم

ماشین رمز لورنز SZ42 که تات موفق به شکست رمز آن شد

زمانی که جنگ جهانی دوم آغاز شد، تات در کمبریج مشغول به تحقیق در زمینه شیمی بود. راهنمای او دریافت که مهارت‌های ریاضی او می‌تواند در رمزگشایی کدهای پارک بلچلی مفید باشد. در سال ۱۹۴۱ تات پس از گذراندن دوره آموزشی در مدرسه کد و رمز لندن، مشغول به کار در آنجا شد. او تعدادی از کدهای رمزنگاری نظامی آلمان را که دولت انگلیس از آن با نام «فیش» (FISH) یاد می‌کرد را رمزگشایی کرد. این سری از کارهای او تا مدت زیادی پنهان نگه داشته شده بود، ولی او در سال ۱۹۹۷ در تولد ۸۰ سالگی‌اش از آن سخن گفت.

پس از جنگ

پس از پایان جنگ جهانی دوم تات به کمبریج بازگشت، ولی نه به قصد اتمام تحصیلات در زمینه شیمی، بلکه تصمیم گرفت تا دکترای خود را در ریاضیات دریافت کند. با اینکه تحصیلات رسمی در زمینه ریاضیات نداشت، ولی ترینیتی کالج او را برای تحقیقات در زمینه ریاضیات پذیرفت. او در زمینه‌های نظریه گراف و جبر به تحقیق پرداخت، که با ترکیب این دو توانست اولین مشارکت برجسته خود در زمینه نظریه ماتروید ارائه دهد.

او در سال ۱۹۴۸ دکترای خود را دریافت کرد. دونالد کوکستر از دانشگاه تورنتو برخی از مقالات تات را مرور کرده بود، و پس از اینکه تات دکترای خود را دریافت کرد، از او برای قبول موقعیتی در دانشگاه تورنتو دعوت کرد. در سال بعد تات با دوروثیا میچل ازدواج کرد.

تات تا سال ۱۹۶۲ در دانشگاه تورنتو ماند، و سپس به هیئت علمی دانشگاه واترلو پیوست. در این زمان تنها ۵ سال از تأسیس این دانشگاه می‌گذشت. تات در تأسیس دانشکده ریاضیات این دانشگاه در سال ۱۹۶۷ نقش بزرگی داشت، و یکی از اولین اعضای دپارتمان ترکیبیات و بهینه‌سازی بود. او به همراه همسرش به خانه‌ای در مونتروز غربی نقل‌مکان کرد، و تا زمان بازنشستگی‌اش در سال ۱۹۸۴، و سپس تا زمان فوت همسرش در سال ۱۹۹۴، در آنجا ماند.

در سال ۱۹۹۶، او به شهر تولد خود در نیومارکت، سافولک، انگلستان بازگشت، ولی باز در سال ۲۰۰۰ به واترلو، کانادا بازگشت که دو سال پس از آن در سال ۲۰۰۲ فوت کرد.

تأثیر تات

پال سیمور از دانشگاه پرینستون می‌گوید:

«پروفسور تات سال‌های زیادی شخص برجسته‌ای در نظریه گراف بود، و مشارکت‌های او در این موضوع از هر شخص دیگری مهم‌تر بوده‌است (به هر لحاظ به غیر از تعداد). موارد زیادی هست که تات در شاخه‌ای دست نخورده از نظریه گراف نتیجه زیبایی یافته‌است، و در بسیاری از موارد منجر به ایجاد رشته مهم جدیدی شده‌است.»

لاسلو لوواس می‌گوید:

«تعداد کمی از قضیه‌های ریاضی به افتخار شخصی که آن را اثبات کرده‌است نام‌گذاری شده‌اند. اما در مورد تات، چندین نتیجه این چنین وجود دارد: برای کسی که در زمینه نظریه تطابق کار می‌کند، قضیه تات مشخصه شناسایی گراف‌های دارای تطابق ایدئال است. برای کسی که در زمینه نظریه ماتروید کار می‌کند، قضیه تات، ویژگی ماترویدهای منظم را بیان می‌کند. برای کسی که به مطالعه دورهای همیلتونی می‌پردازد، قضیه تات به این معنی است که هر گراف مسطح ۴-همبند دارای دور همیلتونی است. همچنین چندجمله‌ای تات برای یک گراف (و یک ماتروید) که یک اصطلاح رایج بین ترکیبیات‌دان‌ها است.»

تات مدال توری (Tory Medal) را توسط جامعه سلطنتی کانادا در سال ۱۹۷۵ دریافت کرد. او برنده جایزه کیلام (Killam Prize) در سال ۱۹۸۲ شد. در سال ۲۰۰۱ او درجه افسری کانادا، و همچنین جایزه مشترک مؤسسه تحقیقات ریاضی، مؤسسه فیلدز، مؤسسه علوم ریاضی پاسیفیک را دریافت کرد.

نتایج ریاضی

قطعه‌ها و گراف‌های همیلتونی

گراف تات - گرافی که تات برای نقض حدس تایت استفاده کرده بود

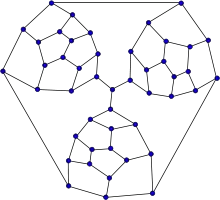
مسئله اینکه آیا یک گراف دارای دور همیلتونی است یا نه، یکی از مسئله‌های ان‌پی کامل است. یک گراف با بیش از ${\displaystyle k}$ راس را k-همبند گوییم اگر آن را نتوان با حذف ${\displaystyle k-1}$ راس ناهمبند کرد.

در سال ۱۸۸۴، پیتر گوتری تایت حدس زد که هر گراف مکعبی سه‌همبند مسطح دارای یک دور همیلتونی است. تات به تفکر دربارهٔ حدس تایت پرداخت و توانست مثال نقضی برای آن بیابد.

تات در پایان‌نامه خود، مفهوم «قطعه» (fragment) را معرفی کرد. در دور ${\displaystyle C}$ از گراف ${\displaystyle G}$، قطعه‌ای از ${\displaystyle C}$ یا شامل یالی که در ${\displaystyle C}$ نیست ولی دو راس از ${\displaystyle C}$ را متصل می‌کند هست، یا شامل مؤلفه ${\displaystyle Q}$ در ${\displaystyle G-V(C)}$ همراه با تمام یال‌های از رأس‌های ${\displaystyle Q}$ به رأس‌های ${\displaystyle C}$ است.

در سال ۱۹۵۶، تات با استفاده از مفهوم قطعه اثبات کرد که هر گراف مسطح ۴-همبند همیلتونی است.

قضیه ۱-عامل

یک ۱-عامل (1-factor) گراف ${\displaystyle G}$ که دارای ${\displaystyle n}$ راس است مجموعه‌ای از ${\displaystyle n/2}$ یال مجزا است که انتهای آن‌ها همه رأس‌های گراف را بپوشانند.

قضیه ۱-عامل تات (سال ۱۹۴۷) بیان می‌کند که گراف ${\displaystyle G}$ دارای ۱-عامل است اگر و تنها اگر به ازای هر زیرمجموعه ${\displaystyle U}$ از رأس‌های گراف ${\displaystyle V}$، گراف القاء شده توسط ${\displaystyle V-U}$ حداکثر پارای ${\displaystyle |U|}$ مؤلفه همبند با تعداد راس فرد است.

برازش گراف‌ها

یک برازش گراف در صفحه را محدب گوییم اگر هر کدام وجه‌های آن یک چندضلعی محدب تشکیل دهند. تات (۱۹۶۰، ۱۹۶۳) نشان داد که هر گراف مسطح سه‌همبند دارای یک برازش محدب است. او همچنین نشان داد که اگر ${\displaystyle G}$ گرافی سه‌همبند بدون هیچ زیرتقسیمی از ${\displaystyle K_{5}}$ یا ${\displaystyle K_{3,3}}$ باشد، آن‌گاه ${\displaystyle G}$ دارای یک برازش محدب در صفحه است به‌طوری‌که هیچ سه راس آن در یک خط قرار نگیرند.

تقسیم ایدئال مربع به مربع‌ها

دیاگرام اسمیث

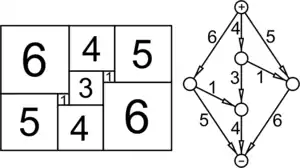
تقسیم ایدئال یک مربع به مربع‌ها تقسیم مربعی به مربع‌های کوچک‌تر است به صورتی که هر کدام از مربع‌های کوچک‌تر اندازه متفاوتی داشته باشند.

تات و چند تن از دوستانش این مسئله را مطالعه کردند و این مسئله را به یک مدار الکتریکی معادل تبدیل کردند. این نمودار را «دیاگرام اسمیث» نام‌گذاری کردند. در این نمودار، هر کدام از مربع‌ها به صورت مقاومتی در نظر گرفته شده بود که به همسایه‌هایش در یال‌های بالایی و پایینی متصل شده بود. سپس قوانین کیرشهف و روش‌های تجزیه مدار را به کار بردند.

تألیفات

کتاب‌ها

• (۱۹۶۶) هم‌بندی در گراف‌ها
• (۱۹۷۱) مقدمه‌ای بر نظریه ماترویدها
• (۱۹۸۴) نظریه گراف
• (۱۹۹۸) نظریه گراف آن‌گونه که من شناخته‌ام

مقالات

• (۱۹۴۷) فاکتوربندی گراف‌های خطی
• (۱۹۵۴) مشارکتی در نظریه چندجمله‌ای‌های رنگی
• (۱۹۶۰) نمایش محدب گراف‌ها
• (۱۹۶۱) مسئله تجزیه گراف به عامل‌های هم‌بند
• (۱۹۶۳) چگونه یک گراف رسم کنیم
• (۱۹۶۳) سرشماری نقشه‌های مسطح

منابع

• تاریخ ریاضیات مک‌توتر - زندگی‌نامه تات
• یادبود تات
• بیوگرافی پروفسور تات