کدگذاری گولومب
کدگذاری[1] گولومب (به انگلیسی: Golomb coding) یا رمزگذاری گولومب یک روش فشرده سازی بدون اتلاف اطلاعات است از خانوادهای از رمزهای فشرده سازی داده که توسط سلیمان دبلیو گلومب در دهه 1960 ابداع شده است. حروف الفبایی از یک توزیع هندسی تبعیت میکنند، از رمزنگاری Golomb به عنوان یک رمز پیشوندی مطلوب استفاده می کنند[2]. باعث میشود که رمزگذاری Golomb بسیار مناسب برای موقعیتهایی باشد که در آن احتمال وقوع مقادیر کوچک در جریان ورودی، به طور قابل توجهی نسبت به مقادیر بزرگ بیشتر است.
رمزگذاری رایس
رمزگذاری Rice (اختراع شده توسط رابرت اف. رایس ) به استفاده از زیرمجموعهای از خانواده کدهای Golomb، برای تولید یک رمز پیشوندی سادهتر (اما نه لزوما بهینه) اشاره دارد. رایس از این مجموعه رمزها در یک قالب رمز گذاری انطباقی استفاده کرد. منظور از "رمزگذاری رایس" همچنین میتواند آن قالب رمزگذاری انطباقی و یا استفاده از آن زیر مجموعه از کدهای Golomb باشد. در حالی که رمزگذاری Golomb دارای یک پارامتر قابل تنظیم است که میتواند هر عدد صحیح مثبت باشد، کدهای رایس آنهایی هستند که پارامتر قابل تنظیم آن، عددی به صورت است. از آنجایی که کامپیوترها با منطق دودویی کار میکنند، این امر باعث میشود تا رمزگذاری رایس برای استفاده در کامپیوتر بسیار راحت باشد زیرا به راحتی میتوان آن را در عدد 2 ضرب و تقسیم کرد.
رایس بسیار علاقهمند بود تا این زیرمجموعه سادهتر را ارائه کند؛ به این دلیل که توزیعهای هندسی اغلب با زمان تغییر میکنند، یا که دقیقاً شناخته شده نیستند و یا هر دو. بنابراین انتخاب رمز به ظاهر بهینه ممکن است چندان سودمند نباشد.
رمزگذاری رایس به عنوان مرحله رمزگذاری آنتروپی در تعدادی از روش های فشرده سازی تصویر بدون اتلاف و فشرده سازی دادههای صوتی استفاده میشود.
بررسی کلی
ساختار کدها
رمزگذاری Golomb از یک پارامتر قابل تنظیم برای تقسیم مقدار ورودی به دو بخش استفاده میکند: ، نتیجه تقسیم توسط و ، باقیمانده. خارج قسمت در قالب رمزگذاری یگانی (unary) و به دنبال آن مقدار باقیمانده در رمزگذاری دودویی منقطع قرار میگیرد. اگر باشد، کدگذاری Golomb معادل کدگذاری یگانی است.

رمزهای Golomb-Rice را میتوان به عنوان رمزهایی در نظر گرفت که عددی را مشخص میکند که در موقعیت ، و آفست قرار دارد. شکل بالا موقعیت q و افست r را برای رمزگذاری عدد صحیح N با استفاده از پارامتر M در روش Golomb-Rice را نشان می دهد.
عموماً، این دو بخش با عبارات زیر بیان میشوند، به طوری که عددی است که میبایست رمزگذاری شود:
و
- .
نتیجه نهایی به صورت رو به روست: .
توجه داشته باشید که میتواند متشکل از مقادیر متفاوتی از نظر تعداد بیتها باشد. به طور مشخص، برای رمزگذاری رایس تنها دارای b بیت است و برای رمزگذاری Golomb بین b-1 و b بیت متغیر است (یعنی M عددی به صورت نیست). فرض کنید باشد. اگر باشد، باید از b-1 بیت برای رمزگذاری r استفاده شود. اگر باشد باید از b بیت برای رمزگذاری r استفاده کنیم. واضح است که اگر M عددی به صورت باشد، است. همچنین میتوانیم تمام مقادیر r را با b بیت رمزگذاری کنیم.
پارامتر M تابعی از فرآیند برنولی متناظر آن است، که به صورت احتمال موفقیت در یک آزمایش برنولی معین، به صورت پارامتری به شکل میباشد. M یا میانه توزیع و یا میانه 1± است. با استفاده از این نابرابریها قابل تعیین است:
که با کمک عبارت زیر حل میشود
- .
رمزنگاری Golomb برای این توزیع معادل رمزگذاری هافمن برای احتمالات مشابه است؛ اگر این امکان وجود داشت که رمز هافمن را محاسبه کنیم.
استفاده با اعداد صحیح علامت دار
طرحواره Golomb طوری طراحی شده بود تا دنبالهای از اعداد غیر منفی را رمزگذاری کند. با این وجود، به راحتی میتوان آن را با استفاده از یک طرح همپوشانی و درهمآمیزی طوری بسط داد تا برای دنباله های دارای اعداد منفی نیز آن را بپذیریم. که در آن تمام مقادیر با روشی خاص و برگشت پذیر به اعداد مثبت نگاشت میشوند. دنباله اینگونه آغاز میشود: 0، 1-، 1، 2-، 2، 3-، 3، 4-، 4 ... . n اُمین عدد منفی (یعنی n-) به n اُمین عدد فرد (یعنی 2n-1) و m اُمین مقدار مثبت به m اُمین عدد زوج (یعنی 2m) نگاشت میشود. این روند به صورت ریاضی به این صورت بیان شود: یک مقدار مثبت نگاشت شده است به ( ) و یک مقدار منفی نگاشت شده است به ( ) چنین نگاشتی ممکن است برای سادگی استفاده شود، حتی اگر بهینهترین حالت ممکن نباشد. رمزهایی که برای توزیعهای هندسی دو طرفه واقعاً بهینه باشند، شامل انواع مختلفی از رمز Golomb هستند، بسته به اینکه پارامترهای توزیع چه باشند؛ از جمله همین مورد. [3]
الگوریتم ساده
به روش زیر توجه کنید. این رمزگذاری Rice-Golomb است، به طوری که رمز باقیمانده از رمزگذاری دودویی منقطع ساده استفاده میکند، که همچنین با نام "رمزگذاری رایس" نیز شناخته میشود (سایر رمزگذاری های با طول متغیر دودویی، مانند رمزگذاری های حسابی یا هافمن، برای رمزهای باقیمانده نیز امکان پذیر است؛ اگر توزیع آماری رمزهای باقیمانده خطی و مسطح نباشد، و خصوصاً وقتی که همه باقیماندههای ممکن بعد از تقسیم استفاده نشده باشند). در این الگوریتم، اگر پارامتر M عددی به صورت باشد، معادل ساده ای از رمزگذاری رایس میشود.
- پارامتر M را بر روی یک عدد صحیح ثابت قرار بده.
- برای N (عددی که باید رمزگذاری شود)، تعیین کن:
- [quotient = q = int[N/M
- remainder = r = N%M
- Codeword تولید کن
- قالب رمز: <Quotient Code> <Code Remainder> ، به صورتی که:
- رمز Quotient در رمزنگاری یگانی (unary):
- رشتهای به طول q از بیت 1 بنویس (جایگزین: رشتهای از بیت 0)
- یک بیت 0 بنویس (یا متناظراً یک بیت 1)
- رمز Remainder (در رمزگذاری دودویی منقطع )
-
- اگر بود: r را با استفاده از b بیت در نمایش دودویی رمز کن.
- اگر بود: رقم را در نمایش دودویی با استفاده از b بیت 1 رمز کن.
-
مثال
فرض کنید M = 10 باشد. بدین ترتیب . به طور خلاصه:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
به عنوان مثال، با رمزگذاری Rice-Golomb با تعیین M = 10، عدد 42 در مبنای 10، ابتدا به q = 4 ،r = 2 تقسیم میشود و اینگونه رمزگذاری میشود:(لازم نیست که ویرگول جداکننده را در جریان خروجی رمزگذاری کنید، زیرا 0 در انتهای کد q برای تعیین زمانی که q به پایان می رسد و r شروع می شود کفایت میکند؛ هر دو رمز qcode و rcode خودمحدودکننده هستند).
استفاده برای رمزگذاری به میزان زمان اجرا
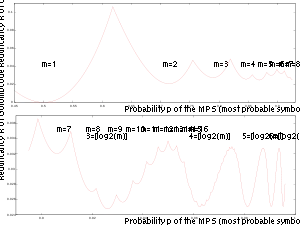
الفبایی شامل دو نماد یا مجموعه ای از دو رویدادِ P و Q به ترتیب با احتمالهای p و ، به طوری که داده شده است. رمزگذاری Golomb میتواند برای رمزگذاری تعدادی صفر یا چند P که توسط Q های تکی از هم جدا شده استفاده شود. در این کاربرد، بهترین مقدار پارامتر M، نزدیکترین عدد صحیح به است . وقتی p = 1/2 ،M = 1 باشند و کد Golomb با یگانی مطابقت دارد ( تا P و به دنبال آن یک Q به صورت n تا یک و به دنبال آن یک صفر رمزگذاری میشود). اگر رمز سادهتر مد نظر باشد، میتوان پارامتر در Golomb-Rice (یعنی پارامتر گولومب) را مساوی نزدیکترین عدد صحیح به قرار داد؛ اگرچه ممکن است همیشه بهترین مقدار نباشد، اما معمولاً بهترین مقدار برای Rice است و عملکرد فشرده سازی آن خیلی نزدیک به رمز گولومبِ بهینه است. (خود رایس پیشنهاد داد تا از رمزهای مختلف برای داده های یکسان استفاده شود تا بفهمیم کدام یک بهترین روش است. بعد تر، محققی از آزمایشگاه JPL روشهای مختلفی را برای بهینه سازی یا تخمین پارامتر برای رمز ارائه داد. )
استفاده از رمز رایس با یک قسمت دودویی که بیت برای به دنباله های رمزگذاری طول اجرا به طوری که در آن P دارای احتمال باشد را در نظر بگیرید. اگر احتمال این باشد که یک بیت بخشی از یک دنباله تایی باشد ( تا P و یک Q) و نرخ فشرده سازی آن دنباله باشد، سپس نرخ فشرده سازی مورد انتظار به صورت زیر است:
فشرده سازی اغلب این گونه بیان می شود: ، نسبت فشرده شده است. برای ، روش رمزگذاری طول اجرا در نسبت فشرده سازی به آنتروپی نزدیک میشود. به عنوان مثال، با در استفاده از کد رایس، تعیین برای ، بازده برای فشرده سازی را نتیجه میدهد، در حالی که حد آنتروپی است.
رمزگذاری گولومب-رایسِ طول اجرای انطباقی
هنگامی که توزیع احتمال برای اعداد صحیح شناخته شده نیست، نمی توان پارامتر بهینه برای رمزگذار Golomb-Rice را تعیین کرد. بنابراین، در بسیاری از برنامهها، از یک رویکردِ دو-گذر استفاده میشود: اول، بلوک داده اسکن میشود تا یک تابع چگالی احتمال (PDF) برای دادهها را تخمین بزند. سپس پارامتر Golomb-Rice از PDF تخمین زده شده تعیین میشود. نوع سادهتر آن است که فرض کنیم PDF متعلق به یک خانواده پارامتری شده است، پارامترهای PDF را از داده ها برآورد کنیم، و سپس پارامتر بهینه Golomb-Rice را محاسبه کنیم. این رویکردی است که مورد استفاده در اکثر برنامه های مورد بحث در زیر است.
یک روش جایگزین برای اینکه داده های عدد صحیح که PDF آن مشخص نیست یا متغیر است را با بازدهی بالا رمزگذاری کنیم این است از رمزگذار سازگار-برگشتی استفاده کنیم. روش Run-length Golomb-Rice (RLGR) با استفاده از یک الگوریتم بسیار ساده که پارامتر Golomb-Rice را بر اساس آخرین نماد رمز شده، کم و زیاد میکند، این نتیجه را بدست میآورد. یک رمزگشا نیز میتواند از همان قاعده پیروی کند تا تغییرات پارامترهای رمزگذاری را ردیابی کند، بنابراین هیچ اطلاعات جانبی بجز داده های رمزگذاری، لازم نیست که منتقل شود. با فرض یک PDF Gaussian عمومی شده، که طیف گستردهای از آماری را که در دادههایی از قبیل خطاهای پیشبینی دیده میشود یا ضرایب تبدیلشده در کدکهای چندرسانهای را نشان میدهد، الگوریتم رمزگذاری RLGR میتواند در چنین برنامه هایی عملکرد بسیار خوبی داشته باشد.
استفاده ها
تعداد بیشماری از رمزگذارهای سیگنال از رمز رایس برای باقی ماندههای پیش بینی استفاده میکنند. در الگوریتمهای پیشبینی، چنین باقیماندههایی معمولاً در یک توزیع هندسی دو طرفه قرار میگیرند، در مقایسه با باقیمانده های بزرگ، باقی مانده های کوچک بیشتر از متداول هستند، و رمز رایس تخمین نزدیکی از رمز Huffman برای چنین توزیعی بدست میآورد با این تفاوت که سربار اینکه مجبور باشیم جدول هافمن را هم منتقل کنیم را نداریم. یک سیگنال که با هیچ توزیع هندسیای مطابقت ندارد، یک موج سینوسی است، زیرا باقیماندههای دیفرانسیل یک سیگنال سینوسی ایجاد میکنند که مقادیر آن ایجاد یک توزیع هندسی نمیکنند (بالاترین و پایینترین مقادیر باقیمانده به طور مشابه دارای تکرار بالایی هستند، فقط مقادیر میانه مثبت و باقیماندههای منفی کمتر اتفاق می افتند).
چندین کدک صوتی بدون اتلاف، مانند Shorten، [4] FLAC ، [5] Apple Lossless و MPEG-4 ALS، بعد از مرحله پیش بینی خطی (که نام آن در Apple Lossless، "فیلتر تطبیقی FIR" است) از یک رمزگذاری رایس استفاده می کنند. همچنین از رمزگذاری رایس در کدک تصویری بدون اتلاف FELICS استفاده میشود.
رمزگذار Golomb-Rice در مرحله رمزگذاری آنتروپی کدگذاری بدون اتلاف تصاویر که مبتنی بر الگوریتم رایس هستند، استفاده میشود. یکی از این آزمایشها منتج به نمودار نسبت فشردهسازی میشود که در پایین آمده است. نوشته های دیگر در این موضوع را در پایین همین صفحه مشاهده کنید. در این فشرده سازیها، داده های دیفرانسیل فضای مترقی مجموعه ای متناوب از مقادیر مثبت و منفی در نزدیکی عدد 0 به دست می آورند، که به اعداد صحیح مثبت نگاشت میشوند (با دو برابر کردن مقدار مطلق و اضافه کردن عدد یک اگر ورودی منفی باشد) و سپس رمزگذاری رایس-گولومب با تغییر دادن مقسومعلیه که کوچک باقی میماند، اعمال میشود.
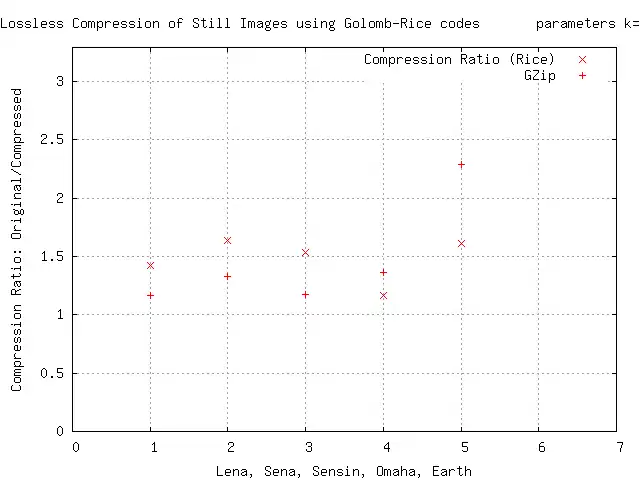
در این نتایج متوجه میشویم، رمزگذاری رایس ممکن است دنبالههای بسیار طولانی از بیت 1 را برای خارجقسمت ایجاد کند. در عمل، اغلب لازم است که طول کل دنباله بیتهایی از 1، محدود شود؛ بنابراین یک نسخه اصلاح شده از رمزگذاری Rice-Golomb شامل جایگزین کردن رشته طولانی بیت 1 با رمزگذاری طول آن رشته توسط یک رمزگذاری بازگشتی رایس-گلومب است. برای انجام این کار لازم است برخی از مقادیر علاوه بر مقسوم علیه اولیه k، رزرو شوند تا تمایز لازم را ممکنسازد.
طرحواره JPEG-LS از رمز Rice-Golomb برای رمزگذاری باقیماندههای پیشبینی استفاده میکند.
(Run-length Golomb-Rice (RLGR نسخه تطبیقی از رمزگذاری Golomb-Rice که در بالا به آن اشاره شد، برای رمزگذاری محتوایات صفحه نمایش در ماشینهای مجازی در اجزای RemoteFX پروتکل دسکتاپ از راه دور مایکروسافت مورد استفاده قرار میگیرد.
همچنین ببینید
- رمزگذاری الیاس دلتا (δ)
پیوند به بیرون
- صفحه وب با نمونهای عملی از رمزگذاری و رمزگشایی Golomb.
- «کُدگذاری» [رایانه و فنّاوری اطلاعات] همارزِ «coding»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر دوم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۶۴-۷۵۳۱-۳۷-۰ (ذیل سرواژهٔ کُدگذاری)
- Gallager, R. G.; van Voorhis, D. C. (1975). "Optimal source codes for geometrically distributed integer alphabets". IEEE Transactions on Information Theory. 21 (2): 228–230. doi:10.1109/tit.1975.1055357.
- Merhav, N.; Seroussi, G.; Weinberger, M. J. (2000). "Coding of sources with two-sided geometric distributions and unknown parameters". IEEE Transactions on Information Theory. 46 (1): 229–236. doi:10.1109/18.817520.
- "man shorten". Archived from the original on 2014-01-30. Retrieved 2008-12-07.
- FLAC documentation: format overview