اساچای-۳
اساچای۳ (الگوریتم امن درهمساز ۳) آخرین عضو خانواده الگوریتم امن درهمساز است که توسط مؤسسه ملی فناوری و استانداردها در ۵ اوت ۲۰۱۵ منتشر شد.[3][4] ساختار داخلی اساچای۳ با ساختار اساچای-۱ و اساچای-۲ که بیشتر شبیه امدی۵ میباشند تفاوت دارد، اگرچه عضوی از همان سری استانداردها محسوب میشود.
| الگوریتم های ایمن درهمساز | |
|---|---|
| مفاهیم | |
| توابع درهمساز · اساچای · دیاساِی | |
| استانداردهای اصلی | |
| اساچای۰ · اساچای۱ · اساچای۲ · اساچای-۳ | |
| عمومی | |
|---|---|
| طراحان | گیدو برتونی, جوان دیمِن, مایکل پیترز و ژیل وان آش. |
| تاریخ اولین انتشار | ۲۰۱۵ |
| بهترین تحلیل رمز منتشر شده | |
| حمله پیش نمایش به کچاک-۵۱۲ به ۸ دور کاهش یافت که به ۵۱۱.۵ ۲ زمان و ۵۰۸ ۲ حافظه نیاز دارد.[1]. تمایزدهندههای دارای مجموع صفر برای یک Keccak-f [1600] کامل ۲۴ دوره وجود دارند، اگرچه نمی توان از آنها برای حمله به خود تابع درهمساز استفاده کرد. [2] | |
اساچای۳ یک زیر مجموعه از خانواده بدوی گستردهتر رمزنگاری Keccak(/ˈkɛtʃæk, -ɑːk/) است،[5][6] که توسط گیدو برتونی، جوان دیمِن، مایکل پیترز و ژیل وان آش طراحی شده و بر روی RadioGatún بنا شدهاند. نویسندگان Keccak کاربردهای اضافی برای این تابع ارائه دادهاند، که البته هنوز توسط NIST استاندارد نشدهاند، از جمله رمز دنبالهای، یک سیستم رمزگذاری تأیید هویت، یک برنامه درهمساز «درختی» برای درهمسازی سریعتر بر روی برخی معماریهای خاص،[7][8] و رمزهای AEAD کیاک(Keyak) و کِتجه(Ketje).[9][10]
Keccak مبتنی بر یک رویکرد جدید به نام ساخت اسفنجی است.[11] ساخت اسفنجی مبتنی بر یک تابع تصادفی گسترده تصادفی یا جایگشت تصادفی است و این امکان را میدهد که هر مقدار از داده وارد شود("جذب" در اصطلاحات اسفنجی)، و هر مقدار از داده بیرون انداخته شود("فشردن")، در حالی که با توجه به همه ورودیهای قبلی به عنوان یک تابع نیمه تصادفی عمل میکند. این منجر به انعطافپذیری زیادی میشود.
NIST در حال حاضر برنامه ای برای برداشت اساچای۲ یا حذف آن از استاندارد اصلاح شده ایمن درهمسازی ندارد. هدف از اساچای۳ این است که میتواند در برنامههای فعلی در صورت لزوم مستقیماً جایگزین اساچای۲ شود و استحکام ابزار کلی الگوریتم درهمساز NIST را به طرز قابل توجهی بهبود بخشد.[12]
سازندگان الگوریتمهای Keccak و توابع اساچای۳ پیشنهاد میکنند از تابع سریعتر KangarooTwelve با پارامترهای تنظیم شده و حالت درهمسازی درختی جدید بدون سربار اضافی، برای پیامهای با اندازه کوچک استفاده کنند.
تاریخچه
الگوریتم Keccak اثری از گیدو برتونی، جوان دیمِن (که وی همچنین رمزنگاری Rijndael را با همکاری وینسنت رجمن طراحی کرده)، مایکل پیترز، و ژیل وان آش میباشد. این الگوریتم مبتنی بر طرحهای درهمسازی قبلی PANAMA و RadioGatún است. PANAMA در سال ۱۹۹۸ توسط دیمِن و کریگ کلَپ طراحی شدهاست. RadioGatún، جانشین PANAMA، توسط پیترز، دیمِن و وان آش طراحی شد و در کارگاه NIST Hash در سال ۲۰۰۶ ارائه شد.[13] کد منبع اجرای مرجع از طریق چشم پوشی CC0 به حوزه عمومی اختصاص داده شده است.[14]
در سال ۲۰۰۶، NIST برای ایجاد یک استاندارد جدید درهمسازی، اساچای۳، اقدام به سازماندهی رقابت تابع درهمسازی NIST کرد. اساچای۳ قرار نیست که جایگزین اساچای۲ شود، زیرا هیچ حمله قابل توجهی به اساچای۲ نشان داده نشدهاست. به دلیل حملات موفقیتآمیز بر اساچای۰، امدی۵ واساچای۱،[15][16] NIST احساس نیاز به یک رمزنگاری درهمساز جایگزین و متفاوت کرد، که SHA-3 نام گرفت.
پس از یک دوره تنظیم، پذیرشها باید تا پایان سال ۲۰۰۸ ارسال میشدند. کچاک(Keccak) به عنوان یکی از ۵۱ نامزد پذیرفته شد. در ژانویه ۲۰۰۹، ۱۴ الگوریتم برای دور دوم انتخاب شد. کچاک به آخرین مرحله در دسامبر ۲۰۱۰ رسید.[17]
در طول مسابقه، به شرکت کنندگان اجازه داده شد الگوریتمهایشان را «اصلاح» کنند تا مشکلاتی که کشف شده بود حل شوند. تغییراتی که در کچاک ایجاد شدهاست به این شرح است:[18][19]
- تعداد دورها از 12 + ℓ به 12 + 2ℓ افزایش یافت تا از نظر امنیتی محافظه کارتر باشد.
- message padding از یک طرح پیچیدهتر به الگوی ساده 1 * 10 که در زیر شرح داده شده تغییر یافت.
- نرخ r به جای گرد کردن پایین به نزدیکترین توان ۲، به حد امنیتی (security limit) افزایش یافت.
در تاریخ ۲ اکتبر ۲۰۱۲، کچاک به عنوان برنده مسابقه انتخاب شد.[5]
در سال ۲۰۱۴، NIST پیش نویس FIPS 202 «استاندارد SHA-3: توابع هش مبتنی بر permutation و توابع خروجی قابل گسترش» را منتشر کرد.[20] FIPS 202 در ۵ اوت ۲۰۱۵ تصویب شد.[21]
در ۵ اوت ۲۰۱۵، NIST اعلام کرد که اساچای۳ به یک استاندارد درهمسازی تبدیل شدهاست.[22]
طرح
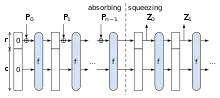
اساچای۳ از ساخت اسفنجی استفاده میکند،[11] که در آن دادهها «جذب» اسفنج میشوند، سپس نتیجهٔ آنها به بیرون «فشرده» میشود. در مرحله جذب، بلوکهای پیام XOR شده و به زیر مجموعه ای از حالت تبدیل میشوند، که بعداً با استفاده از یک تابع جایگشت به صورت یک کل درمیآیند. در مرحله «فشردن»، بلوکهای خروجی از همان زیر مجموعه حالت خوانده میشوند، و با استفاده از تابع تغییر حالت تغییر مییابند. سایز بخشی از حالت که نوشته شده و خوانده شدهاست «نرخ» (مشخص شده با ) نامیده میشود، و اندازه بخشی که توسط ورودی / خروجی دست نخورده میماند، «ظرفیت» (مشخص شده با ) نامیده میشود. ظرفیت تعیینکننده امنیت طرح است. حداکثر سطح امنیتی برابر نصف ظرفیت است.
با درنظر گرفتن یک رشته بیت ورودی ، یک تابع پدینگ مانند ، یک تابع جایگشت که روی بلوکهای بیتی با عرض کار میکند، نرخ و طول خروجی ، ظرفیتی برابر با و ساخت اسفنجی را داریم، میدهد رشتهٔ بیتی به طول ، که به شرح زیر کار میکند:[23] :18
- پرکردن ورودی N با استفاده از تابع pad، که درنتیجه یک padded bit string مانند P با طولی بخش پذیر بر (به طوری که عدد صحیح باشد) میدهد.
- شکستن P به n قطعه متوالی r بیتی P0, … , Pn−1
- مقداردهی اولیه وضعیت S به یک رشته که b بیت از آن مقدار صفر دارند
- ورودی را جذب حالت کنید: برای هر بلوک Pi:
- گسترش P i در پایان توسط یک رشته از c بیت از آن مقدار صفر دارند، که یک رشته با طول b تولید میکند
- XOR آن با S
- تابع جایگشت بلوکی f را روی نتیجه اعمال کنید تا حالت جدید S بدست آید
- Z را به عنوان رشته خالی مقداردهی اولیه کنید
- تازمانیکه که طول Z کمتر از d است:
- r بیت اول از S را به Z اضافه کنید
- اگر Z هنوز کمتر از d بیت طول دارد، f را روی S اعمال کنید، تا حالت S بدست آید
- Z را به d بیت کاهش دهید
این واقعیت که وضعیت داخلی S حاوی c بیت اضافی اطلاعات علاوه بر آنچه در خروجی Z نوشته میشود است، مانع از حملات طولانی مدت میشود که امدی۵، اساچای۱، اساچای۲ و سایر درهمسازیهای مبتنی بر ساخت و ساز مرکل-دامگارد مستعد آن هستند.
در اساچای۳، حالت S شامل یک آرایه ۵ × ۵ شامل کلمات w بیتی (w=۶۴)، و درکل b = ۵ × ۵ × w = ۵ × ۵ × ۶۴ = ۱۶۰۰ بیت است. کچاک(Keccak) همچنین برای کلمههای توان دویی با اندازههای کوچکتر w و حتی با ۱ بیت (که درمجموع حالتی با ۲۵ بیت میسازد) هم تعریف شدهاست. اندازههای حالت کوچک میتواند برای آزمایش حملات تحلیل رمزنگاری مورد استفاده قرار گیرد، و اندازههای حالت متوسط (از w = ۸، با ۲۰۰ بیت، تا w = ۳۲، با ۸۰۰ بیت) در برنامههای کاربردی سبک استفاده میشود.[9][10]
برای موارد اساچای۳–۲۲۴، اساچای۳–۲۵۶، اساچای۳–۳۸۴، و اساچای۳–۵۱۲، مقدار r از d بیشتر است، بنابراین در مرحله فشردن نیازی به جایگشتهای بلوکی اضافی نیست. d بیت اول از وضعیت، همان درهمسازی مورد نظر ما میباشد. با این حال، SHAKE-۱۲۸ و SHAKE-۲۵۶ امکان خروجی با طول دلخواه را به ما میدهند، که در برنامههایی مانند رمزگذاری با پرکردن نامتقارن بهینه مفید است.
لایه گذاری
برای اطمینان از اینکه پیام را میتوان به بلوکهای r بیتی مساوی تقسیم کرد، لایهگذاری لازم است. اساچای۳ از الگوی ۱*۱۰ در عملکرد لایهگذاری خود استفاده میکند: یک بیتِ ۱، بهدنبال آن صفر یا بیشتر بیتِ ۰ (حداکثر r − ۱ تا) و یک بیتِ ۱ نهایی.
حداکثر r − ۱ بیت صفر زمانی رخ میدهد که آخرین بلوک پیام r − ۱ بیت طول داشته باشد. دراینحالت بلوک دیگری پس از بیتِ ۱ اولیه اضافه میشود که حاوی r − ۱ بیتِ صفر قبل از بیتِ ۱ نهایی است.
دو بیتِ ۱، حتی اگر طول پیام در حال حاضر بر r بخشپذیر باشد، اضافه میشوند.[23] :5.1 در این حالت، یک بلوک دیگر به پیام اضافه میشود که حاوی یک بیتِ ۱ است، به دنبال آن یک بلوک r − ۲ تایی بیتِ صفر و یک بیتِ ۱ دیگر میباشد. این کار لازم است برای اینکه که یک پیام که طولش بر r بخش پذیر است و به چیزی که شبیه لایهگذاری به نظر میرسد ختم میشود، همان درهمسازی را تولید نکند که یک پیام دیگری که آن بیتها را ندارد تولید میکند.
بیتِ ۱ اولیه برای این نیاز است که پیامهایی که فقط چند بیتِ ۰ اضافی آخرشان متمایز است، یک درهمسازی مشابه ایجاد نکنند.
موقعیت بیتِ ۱ نهایی نشان میدهد که از کدام نرخ r استفاده شدهاست (لایهگذاری چند نرخی)، که برای اثبات امنیت لازم است تا برای انواع مختلف درهمسازی کار کند. بدون آن، درهمسازیهای مختلف از یک پیام کوتاه یکسان میتواند دارای برش یکسانی شود.
جایگشت بلوکی
تبدیل بلوکی f، که Keccak-f [1600] برای اساچای۳ است، جایگشتی است که از عملیات XOR، AND و NOT استفاده میکند و برای پیادهسازی آسان در هردوی نرمافزار و سختافزار طراحی شدهاست.
این تبدیل برای هر طول کلمهای که توانی از دو باشد، w = 2ℓ تعریف شدهاست. نسخه اصلی اساچای۳، از کلمات ۶۴ بیتی، ℓ = ۶ استفاده میکند.
آرایهٔ حالت میتواند به صورت یک آرایهٔ ۵ × ۵ × w بیتی در نظر گرفته شود. فرض کنید a[i][ j][k] برابر بیتِ (۵i + j) × w + k ام از ورودی باشد، که در یک مدل Little Endian از قرارداد شمارش بیتی و اندیس گذاری ردیف-اول فرض شدهاست، یعنی i شماره ردیف، j شماره ستون و k شماره بیت را مشخص میکند.
اندیس گذاری حسابی برای دو بعد اول، در پیمانه ۵ و برای بعد سوم در پیمانه w انجام میشود.
تابع جایگشت بلوکیِ پایه، متشکل از ۱۲ + ۲ℓ دورِ پنج مرحلهای است:
- θ (تتا)
- اعداد زوج و فرد هر یک از ۵w (برابر ۳۲۰ اگر w = ۶۴) ستون ۵بیتی را حساب کرده و xor آن را با دو ستون مجاورش در یک الگوی منظم محاسبه کنید. بهطور دقیقتر، a[i][ j][k] ← a[i][ j][k] ⊕ parity(a[0...4][ j−1][k]) ⊕ parity(a[0...4][ j+1][k−۱])
- ρ (رو)
- هر کدام از ۲۵ کلمه را با یک عدد مثلثی متمایز مانند ۰، ۱ ، ۳، ۶ ، ۱۰، ۱۵ ،...شیفت دورانی دهید. بهطور دقیق،a[۰][۰] دوران نمییابد، و به ازای هر ۰ ≤ t < ۲۴،
- a[i][ j][k] ← a[i][ j][k−(t+1)(t+۲)/۲]، درصورتی که .
- π (پی)
- ۲۵ کلمه را در یک الگوی ثابت جایگشت دهید a[j][2i+3j] ← a[ i][j]
- χ (خی)
- بیت به یبت با ردیفها ترکیب کنید، با استفاده از رابطهٔ x ← x ⊕ (¬y & z) بهطور دقیق، a[i][ j][k] ← a[i][ j][k] ⊕ (¬a[i][ j+۱][k] & a[i][ j+۲][k]) این تنها عملیات غیر خطی در اساچای۳ است.
- ι (iota)
- یک ثابت دور را با یک کلمه از حالت xor کنید. بهطور دقیق، در دور nام، به ازای ۰ ≤ m ≤ ℓ، مقدار a[0][0][2m−۱] با بیت m + 7nام از یک دنباله اجرایی حاصل از ثبات تغییر بازخورد خطی(LFSR) درجه-۸ xor میشود. این کار تقارنی را که در مراحل دیگر حفظ میشود، میشکند.
سرعت
سرعت درهمسازی پیامهای طولانی توسط اساچای۳، بسیار تحت تأثیر محاسبهٔ f = Keccak-f [۱۶۰۰] و XOR کردن S با مقدار گسترشیافتهٔ P i، که یک عملیات روی b = ۱۶۰۰ بیت است، میباشد. با این حال، از آنجایی که c بیت آخر مقدار گسترشیافتهٔ P i درهرصورت صفر هستند، و XOR با ۰ یک NOP است، کافی است عملیات XOR را فقط برای r بیت انجام دهیم(r = ۱۶۰۰–۲ × ۲۲۴ = ۱۱۵۲ بیت برای اساچای۳–۲۲۴، ۱۰۸۸ بیت برای اساچای۳–۲۵۶، ۸۳۲ بیت برای اساچای۳–۳۸۴ و ۵۷۶ بیت برای اساچای۳–۵۱۲). هرچه r پایینتر باشد (و برعکس، هرچه c = b - r = 1600 - r بالاتر باشد)، درهمسازی ناکارآمدتر و پرهزینهتر اما ایمن تر میشود، زیرا تعداد بیت کمتری از پیام میتواند با حالت XOR شود (یک عملیات سریع) قبل از هر بار استفاده از f که از نظر محاسباتی پرهزینه است. نویسندگان سرعتهای زیر را برای اجرای پیادهسازیهای نرمافزاری Keccak-f [1600] به اضافه XOR کردن ۱۰۲۴بیت گزارش میدهند، که تقریباً با اساچای۳–۲۵۶ مطابقت دارد:
- ۵۷٫۴ cpb در IA-32 , Intel Pentium 3[24]
- ۴۱ cpb در IA-32 + MMX , Intel Pentium ۳۲
- ۲۰ cpb در IA-32 + SSE , Intel Core 2 Duo یا AMD Athlon ۶۴
- ۱۲٫۶ cpb در دستگاه معمولی مبتنی بر x۸۶–۶۴
- ۶–۷ cpb در IA-64[25]
برنشتاین بهطور دقیق برای اساچای۳–۲۵۶ روی x۸۶–۶۴، عدد ۱۱٫۷–۱۲٫۲۵ cpb را بسته به CPU اندازهگیری کردهاست.[26] :7 اساچای۳ به دلیل کند بودن در معماریهای مجموعه دستورالعمل (CPU) که دستورالعمل خاصی برای محاسبه سریعتر توابع Keccak ندارند، مورد انتقاد قرار گرفتهاست - اساچای۲–۵۱۲ بیش از دو برابر سریعتر از اساچای۳، و اساچای۱ بیش از سه برابر سریعتر از آن روی یک پردازنده Intel Skylake با فرکانس کلاک ۳٫۲ گیگاهرتز اجرا میشود.[27] نویسندگان با پیشنهاد استفاده از SHAKE۱۲۸ و SHAKE۲۵۶ به جای اساچای۳–۲۵۶ و اساچای۳–۵۱۲، به قیمت کاهش یافتن نصف مقاومتپیشنمایش (اما با همان مقاومت برخورد)، به این انتقاد واکنش نشان دادهاند. با این کار، عملکرد برابر میشود با اساچای۲–۲۵۶ و اساچای۲–۵۱۲.
با این حال، از نظر پیادهسازی سختافزاری، اساچای۳ به طرز ویژهای سریعتر از سایر فینالیستها است،[28] و همچنین سریع تر از اساچای۲ و اساچای۱.[27]
معماریهای ARMv8[29] و IBM s۳۹۰x در حال حاضر (از سال ۲۰۱۸) شامل دستورالعملهای ویژه ای هستند که الگوریتمهای Keccak را قادر میسازند سریعتر اجرا شوند.
نمونهها
استاندارد NIST نمونههای زیر را برای پیام M و طول خروجی d نشان میدهد:[23] :20,23
| نمونه | طول خروجی d | نرخ r = اندازه بلوک |
ظرفیت c | تعریف | نقاط قوت امنیتی در بیتها | ||
|---|---|---|---|---|---|---|---|
| برخورد | پیش نمایش | پیش نمایش دوم | |||||
| اساچای۳–۲۲۴ (M) | ۲۲۴ | ۱۱۵۲ | ۴۴۸ | | 01, 224) | ۱۱۲ | ۲۲۴ | ۲۲۴ |
| اساچای۳–۲۵۶ (M) | ۲۵۶ | ۱۰۸۸ | ۵۱۲ | | 01, 256) | ۱۲۸ | ۲۵۶ | ۲۵۶ |
| اساچای۳–۳۸۴ (M) | ۳۸۴ | ۸۳۲ | ۷۶۸ | | 01, 384) | ۱۹۲ | ۳۸۴ | ۳۸۴ |
| اساچای۳–۵۱۲ (M) | ۵۱۲ | ۵۷۶ | ۱۰۲۴ | | 01, 512) | ۲۵۶ | ۵۱۲ | ۵۱۲ |
| SHAKE128(M, d) | d | ۱۳۴۴ | ۲۵۶ | | 1111, d) | min(d/2,128) | ≥min(d,128) | min(d,128) |
| SHAKE256(M, d) | d | ۱۰۸۸ | ۵۱۲ | | 1111, d) | min(d/2,256) | ≥min(d,256) | min(d,256) |
با تعاریف زیر
- Keccak[c](N, d)=sponge[Keccak-f[1600], pad10*1, r](N, d)[23] :20
- Keccak-f [1600] = Keccak-p [1600، 24] :۱۷
- c ظرفیت است
- r نرخ است و = ۱۶۰۰ - c میباشد
- N رشته بیت ورودی است
توجه داشته باشید که پسوندهای اضافه شده به صورت رشتههای بیتی نوشته میشوند، نه رقمهای مبنای ۱۶.
نمونههای اساچای۳ جایگزین قطرهای برای اساچای۲ هستند، با همان ادعاهای امنیتی یکسان. نمونههای SHAKE به اصطلاح توابع خروجی قابل گسترش XOF گفته میشوند. به عنوان مثال، SHAKE128(M، ۲۵۶) میتواند به عنوان یک تابع درهمسازی با طول ۲۵۶ بیت و امنیت کلی ۱۲۸بیتی استفاده شود.
توجه داشته باشید که همه نمونهها، تعدادی بیت به پیام اضافه میکنند، که سمت راستترین آنها نشاندهندهٔ پسوند جدایی دامنه است. هدف از این کار این است که اطمینان حاصل شود نمیتوان پیامهایی با همان خروجی درهمسازیشده را برای کاربردهای مختلف برنامه درهمسازی Keccak ساخت. پسوندهای جدایی دامنه زیر موجودند:[23][30]
| پسوند | معنی |
|---|---|
| … ۰ | برای استفاده بعدی محفوظ است |
| ۰۱ | SHA-3 |
| … ۱۱ | RawSHAKE |
RawSHAKE پایه ای است برای رمزگذاری ساکورا جهت درهمسازی درختی، که هنوز استاندارد نشدهاست. با این حال، پسوند SHAKE با دقت انتخاب شدهاست تا اینکه سازگار با نسخههای بعدی ساکورا باشد. قبل از اعمال RawSHAKE، Sakura بیت ۰ را برای یک هاپ زنجیرهای یا بیت ۱ را برای یک پیام، سپس ۱۰*۰ را برای یک گره غیرنهایی (داخلی) یا ۱ را برای یک گره نهایی، اضافه میکند. درهمسازی متوالی مربوط به درخت هاپ با یک گره پیام است، بدین معنی که ۱۱ قبل از اعمال RawSHAKE به پیام اضافه میشود؛ بنابراین، SHAKE XOFs مقدار ۱۱۱۱ را به پیام اضافه میکند، یعنی ۱ برای پیام، ۱ برای گره نهایی و ۱۱ برای پسوند جدایی دامنه RawSHAKE.[30] :16
از آنجا که لایهگذاری ۱۰*۱ همیشه حداقل دو بیت را اضافه میکند، در کتابخانههای مرتب با بایت همیشه شش بیت صفر استفاده نشده وجود دارد؛ بنابراین، این بیتهای اضافی هرگز پیام لایهگذاری را طولانیتر نمیکنند.
نمونههای اضافی
در دسامبر سال ۲۰۱۶، NIST یک سند جدید با نام NIST SP.800-185 منتشر کرد[31] که عملکردهای اضافی مشتق شده اساچای۳ را شرح میدهد:
| نمونه | شرح |
|---|---|
| cSHAKE128 (X , L، N , S) | یک نسخه از SHAKE با پشتیبانی از جداسازی صریح دامنه از طریق پارامترهای شخصیسازی |
| cSHAKE256 (X , L، N , S) | |
| KMAC128 (K , X، L , S) | یک تابع درهمسازی کلید دار بر اساس Keccak. همچنین میتواند بدون کلید به عنوان یک تابع درهمسازی معمولی مورد استفاده قرار گیرد. |
| KMAC256 (K , X، L , S) | |
| KMACXOF128 (K , X، L , S) | |
| KMACXOF256 (K , X، L , S) | |
| TupleHash128 (X , L، S) | یک تابع برای درهمسازی یک چندتایی (تاپل) از رشتهها. خروجی این تابع، هم به محتویات و هم توالی رشتههای ورودی بستگی دارد. |
| TupleHash256 (X , L، S) | |
| TupleHashXOF128 (X , L، S) | |
| TupleHashXOF256 (X , L، S) | |
| ParallelHash128 (X , B، L , S) | یک تابع که به منظور بهرهبرداری از موازیسازی در پردازندههای مدرن حهت درهمسازی سریعتر ساخته شدهاست. بر خلاف KangarooTwelve، از Keccak با دورِکاهشیافته استفاده نمیکند. |
| ParallelHash256 (X , B، L , S) | |
| ParallelHashXOF128 (X , B، L , S) | |
| ParallelHashXOF256 (X , B، L , S) |
- X رشته بیت ورودی اصلی است. این رشته ممکن است هر طولی، از جمله صفر داشته باشد.
- L عدد صحیحی است که تعداد بیت خروجی درخواستی را نشان میدهد.
- N نام یک تابع به صورت رشتهٔ بیتی است که توسط NIST برای تعریف توابع بر اساس cSHAKE استفاده میشود. هنگامی که هیچ تابعی غیر از cSHAKE مورد نظر باشد، N با رشته خالی مقداردهی میشود.
- S یک رشتهٔ بیتی جهت سفارشیسازی است. کاربر این رشته را برای تعریف یک پارامتر متغیر از تابع انتخاب میکند. هنگامی که هیچ سفارشی سازی مورد نظر نیست، S با رشته خالی مقداردهی میشود.
- K یک کلید به صورت رشتهٔ بیتی با هر طولی، از جمله صفر است.
- B تعداد بایتهای هر بلوک حهت درهمسازی موازی است. B میتواند هر عدد صحیحی باشد به طوری که 0 <B <2 2040.
تحولات بعدی
درخت درهمسازی
در سال ۲۰۱۶، همان تیمی که توابع اساچای۳ و الگوریتم Keccak را ایجاد کرده بودند، یک جایگزین سریعتر با تعداد دورهای کاهشیافته (کاهشیافته به ۱۲ و ۱۴دور، از ۲۴ دور در اساچای۳) که به دلیل استفاده از درهمسازی درختی، میتواند از قابلیت اجرای موازی بهره بگیرد، ارائه کردند: KangarooTwelve و MarsupilamiFourteen.[32]
این توابع با ParallelHash، تابع درهمسازی استاندارشده FIPS باقابلیت موازی سازی و مبتنی بر Keccak، از نظر موازیسازی متفاوت است، زیرا در پیامهای با اندازه کوچک سریعتر از ParallelHash هستند.
تعداد دور کاهش یافته با تلاش بسیار زیاد تحلیلی رمزنگاری متمرکز بر Keccak که نتوانست در حمله عملیاتی به هیچ الگوریتم Keccak با تعداد دور نزدیک به دوازده ایجاد کند، تصدیق میشود. این الگوریتمهای با سرعت بالاتر جزئی از اساچای۳ نیستند (زیرا آنها بعداً توسعه یافتهاند)، و بنابراین سازگار با FIPS نیستند. اما آنها به همان اندازه توابع اساچای۳ ایمن هستند، زیرا آنها از همان جایگشت Keccak استفاده میکنند و هیچ حمله ای به Keccak ۱۲ دوری نشدهاست.
KangarooTwelve یک نسخه با تعداد دور کاهش یافته (از ۲۴ به ۱۲ دور) با عملکرد بالاتر از Keccak است که ادعا میکند ۱۲۸ بیت امنیت دارد[33] در حالی که عملکردی برابر با ۰٫۵۵ چرخه در هر بایت دارد.[34] این الگوریتم یک پیش نویس IETF RFC است.[35]
MarsupilamiFourteen، نسخهٔ اندکی تغییریافتهٔ KangarooTwelve، از ۱۴ دور جایگشت Keccak استفاده میکند و ادعا میکند ۲۵۶ بیت امنیت دارد. توجه داشته باشید که امنیت ۲۵۶ بیتی در عمل مفیدتر از امنیت ۱۲۸ بیتی نیست، اما ممکن است طبق برخی استانداردها مورد نیاز باشد.[33] درحال حاضر ۱۲۸ بیت برای پیروزشدن بر حملات brute-force بر روی سختافزار فعلی کافی است، بنابراین داشتن امنیت ۲۵۶ بیتی ارزش عملی نمیافزاید، مگر اینکه کاربر نگران پیشرفتهای چشمگیر سرعت کامپیوترهای کلاسیک باشد. برای مقاومت در برابر رایانههای کوانتومی، به زیر مراجعه کنید.
KangarooTwelve و MarsupilamiFourteen، مشابه SHAKE، توابع با قابلیت گسنرش خروجی هستند، بنابراین آنها برای یک پیام مشترک با طول خروجی متفاوت، خروجی نزدیک به هم تولید میکنند (خروجی طولانیتر تعمیمیافتهٔ خروجی کوتاهتر میباشد). توابع درهمساز مانند اساچای۳ یا ParallelHash (به جز انواع مختلف XOF) چنین خاصیتی از خود نشان نمیدهند.[23]
امنیت در برابر حملات کوانتومی
یک نتیجه کلی (الگوریتم گرور) وجود دارد که کامپیوترهای کوانتومی میتوانند یک حمله پیشنمایش ساختار یافته را در انجام دهند، در حالی که یک حمله brute-force کلاسیک به 2d نیاز دارد. یک حمله ساختار یافته پیشنمایش نشانگر یک حمله پیشنمایش دوم[38] و در نتیجه یک حمله تصادم است. یک کامپیوتر کوانتومی همچنین میتواند یک حمله روز تولد را در [39] (اگرچه این مورد اختلاف است[40]) انجام دهد، درنتیجه مقاومت در برابر تصادم را ازبین ببرد. با توجه به این که حداکثر قدرت میتواند باشد، کرانهای بالای[41] زیر بر روی امنیت کوانتومی اساچای۳ حاصل میشوند:
| نمونه | نقاط قوت امنیتی در بیتها | |||
|---|---|---|---|---|
| تصادم (براسارد و همکاران) |
تصادم (برنشتاین) |
پیش نمایش | پیش نمایش ۲ | |
| SHA3-224 (M) | ۷۴⅔ | ۱۱۲ | ۱۱۲ | ۱۱۲ |
| SHA3-256 (M) | ۸۵⅓ | ۱۲۸ | ۱۲۸ | ۱۲۸ |
| SHA3-384 (M) | ۱۲۸ | ۱۹۲ | ۱۹۲ | ۱۹۲ |
| SHA3-512 (M) | ۱۷۰⅔ | ۲۵۶ | ۲۵۶ | ۲۵۶ |
| SHAKE128(M, d) | min(d/3,128) | min(d/2,128) | ≥min(d/2,128) | min(d/2,128) |
| SHAKE256(M, d) | min(d/3,256) | min(d/2,256) | ≥min(d/2,256) | min(d/2,256) |
نشان داده شدهاست که ساخت و ساز مرکل-دامگورد، که در اساچای۲ از آن استفاده میشود، در حال فروپاشی است و به تبع آن، مقاوم در برابر تصادم کوانتومی است،[42] اما برای ساخت اسفنج مورد استفاده در اساچای۳، نویسندگان فقط برای این مورد که تابع بلوکی f باهزینهکم وارونپذیر نیست اثبات کردهاند. Keccak-f [۱۶۰۰]، ولی، باهزینهکم وارونپذیر است و بنابراین اثبات آنها کاربردی نیست.[43]
بحث و گفتگو در مورد تغییر ظرفیت
در فوریه ۲۰۱۳در کنفرانس RSA، و سپس در اوت ۲۰۱۳ در CHES، NIST اعلام کرد که مقادیر مختلفی را برای ظرفیت، که پارامتر امنیتی است، برای استاندارد اساچای۳، در مقایسه با ارسال اولیه، انتخاب میکنند.[44][45] این تغییرات باعث سردرگمی شد.
مسابقات توابع درهمسازی، خواستار توابع درهمساز شد که حداقل به همان اندازه نمونههای اساچای۲ امنیت داشته باشند. به این معنی که یک خروجی d بیتی باید مقاومت d/۲ بیتی درمقابل حملات تصادم و مقاومت d بیتی در برابر حملات پیشنمایش داشته باشد، مقدار حداکثری که برای d بیت از خروجی دست یافتنی است. اثبات امنیتی Keccak امکان تنظیم سطح امنیتی را مبتنی بر «ظرفیت» c میدهد، که مقاومت c/۲ بیتی در برابر هردو حمله تصادم و حمله پیشنمایش فراهم میکند. جهت برآورده ساختن قوانین اصلی رقابت، نویسندگان کچاک c = ۲d را پیشنهاد کردند. تغییر اعلام شده برای پذیرش همان امنیت d/۲ بیتی برای همه اشکال حمله و استانداردسازی c = d بود. این میتوانست با فراهم کردن امکان درهمسازی d بیت اضافهتر از ورودی درهربار تکرار چرخه، سرعت Keccak را بالا ببرد؛ ولی، توابع درهمسازی دیگر نمیتوانستند جایگزینهای قطرهای با همان مقاومت پیشنمایشی اساچای۲ باشند. با این کار مقاومت پیشنمایشی به نصف کاهش مییافت، باعث میشد در برابر پیشرفتهای محاسبات کوانتومی آسیبپذیر شود، که بهطور مؤثری آن را دوباره به نصف کاهش میداد.[38]
در سپتامبر ۲۰۱۳، دنیل جی برنشتاین در لیست پستی انجمن درهمسازی NIST[46] پیشنهاد کرد که امنیت را با رساندن ظرفیت به ۵۷۶ بیت، که در ابتدا به عنوان پیش فرض کچاک پیشنهاد شده بود، و علاوه بر این در مشخصات فنی اساچای۳ گنجانده نشده بود، تقویت کنند.[47] این کار میتوانست حداقل یک اساچای۳–۲۲۴ و اساچای۳–۲۵۶ با همان مقاومت پیشنمایشی به اندازه پیشینیان اساچای۲ خود فراهم کند، اما اساچای۳–۳۸۴ و اساچای۳–۵۱۲ مقاومت پیشنمایشی بسیار کمتری نسبت به پیشینیان اساچای۲ خود پیدا میکردند. در اواخر ماه سپتامبر، تیم کچاک با بیان اینکه آنها قبلاً امنیت ۱۲۸ بیتی با تعیین c = ۲۵۶ را به عنوان یک گزینه در پروپوزال اساچای۳ خود پیشنهاد دادهبودند، پاسخ داد.[48] اگرچه از نظر آنها کاهش ظرفیت قابل توجیه بود، با توجه به پاسخ منفی، آنها پیشنهاد کردند ظرفیت به c = ۵۱۲ بیت برای همه نمونهها افزایش یابد. این مقدار ظرفیت به همان اندازهٔ هر استاندارد قبلی با حداکثر سطح امنیتی ۲۵۶ بیتی بود، و در عین حال بازده مناسبی هم داشت،[49] اما نه به اندازهٔ مقاومت پیشنمایشی 384- / 512 بیتی ارائه شده توسط اساچای۲–۳۸۴ و اساچای۲–۵۱۲. نویسندگان سعی کردند با این ادعا که "ادعاکردن یا اعتماد بر سطح قدرت امنیتی بالای ۲۵۶ بیت بی معنی است" خود را توجیه کنند.
در اوایل اکتبر ۲۰۱۳، بروس اشنیر با انتقاد از تصمیم NIST مبنی بر تأثیرات مضر آن بر پذیرش الگوریتم، گفت:
There is too much mistrust in the air. NIST risks publishing an algorithm that no one will trust and no one (except those forced) will use.[50]
پل کرولی، رمزنگار و توسعه دهنده ارشد در یک شرکت مستقل توسعه نرمافزار، با گفتن اینکه کچاک قرار است قابل تنظیم باشد و هیچ دلیلی بر وجود سطوح امنیتی مختلف درون یک اصل اولیه وجود ندارد، حمایت خود از این تصمیم را بیان کرد. وی همچنین اضافه کرد:
Yes, it's a bit of a shame for the competition that they demanded a certain security level for entrants, then went to publish a standard with a different one. But there's nothing that can be done to fix that now, except re-opening the competition. Demanding that they stick to their mistake doesn't improve things for anyone.[51]
برخی گمانها نیز مبنی بر ایجاد تغییرات داخلی در کچاک وجود داشت. تیم کچاک این موضوع را روشن کرد و اظهار داشت که پیشنهاد NIST برای اساچای۳ زیرمجموعه ای از خانواده کچاک است که برای آن بشود با استفاده از کد مرجع ارسال شده به مسابقه، بردارهای تست تولید کرد و این پیشنهاد نتیجه یک سری بحثها بین آنها و تیم درهمسازی NIST بود.[52] همچنین، بروس اشنایر اظهارات قبلی خود را اصلاح کرد و گفت:
وقتی نوشتم که NIST «تغییرات داخلی» در الگوریتم ایجاد کردهاست، اشتباه کردم. این بیدقتی من بود. جایگشت کچاک بدون تغییر باقی ماندهاست. آنچه NIST پیشنهاد کرد کاهش ظرفیت تابع درهمسازی جهت کمک به افزایش عملکرد بود. یکی از ویژگیهای خوب کچاک این است که بسیار قابل تنظیم است.[50]
در پاسخ به این بحث و گفتگو، در نوامبر ۲۰۱۳ جان کلسی از NIST پیشنهاد بازگشت به طرح اصلی c = ۲d برای همه نمونههای جایگزینی قطره ای اساچای۲ را داد.[53] این بازبینی در پیش نویس آوریل ۲۰۱۴ تأیید شد.[54] این پیشنهاد در استاندارد انتشار نهایی در اوت ۲۰۱۵ پیادهسازی شد.[3]
فرمهای با ظرفیت کاهشیافته با عنوان SHAKE۱۲۸ و SHAKE۲۵۶ منتشر شدند، که عدد آنها سطح امنیتی را نشان میدهد و تعداد بیتهای خروجی متغیر است، اما باید دو برابر مقاومت موردنیاز در برابر تصادم باشد.
نمونههایی از انواع اساچای۳
مقادیر درهمسازی زیر از NIST.gov است:[55]
SHA3-224 ("")
6b4e03423667dbb73b6e15454f0eb1abd4597f9a1b078e3f5b5a6bc7
SHA3-256 ("")
a7ffc6f8bf1ed76651c14756a061d662f580ff4de43b49fa82d80a4b80f8434a
SHA3-384 ("")
0c63a75b845e4f7d01107d852e4c2485c51a50aaaa94fc61995e71bbee983a2ac3713831264adb47fb6bd1e058d5f004
SHA3-512 ("")
a69f73cca23a9ac5c8b567dc185a756e97c982164fe25859e0d1dcc1475c80a615b2123af1f5f94c11e3e9402c3ac558f500199d95b6d3e301758586281dcd26
SHAKE128 (""، 256)
7f9c2ba4e88f827d616045507605853ed73b8093f6efbc88eb1a6eacfa66ef26
SHAKE256 (""، 512)
46b9dd2b0ba88d13233b3feb743eeb243fcd52ea62b81b82b50c27646ed5762fd75dc4ddd8c0f200cb05019d67b592f6fc821c49479ab4840292eacb3b7c4be
تغییر یک بیت واحد باعث میشود که هر بیت در خروجی با احتمال ۵۰٪ تغییر کند که یک اثر بهمنی را نشان میدهد:
SHAKE128("The quick brown fox jumps over the lazy dog", 256)
f4202e3c5852f9182a0430fd8144f0a74b95e7417ecae17db0f8cfeed0e3e66e
SHAKE128("The quick brown fox jumps over the lazy dof", 256)
853f4538be0db9621a6cea659a06c1107b1f83f02b13d1
مقایسه توابع اساچای
در جدول زیر، حالت داخلی به معنی تعداد بیتهایی است که به بلوک بعدی منتقل میشوند.
| الگوریتم و نوع آن | اندازهی خروجی (تعداد بیت) |
اندازه حالت داخلی (تعداد بیت) |
اندازه بلوک (تعدادبیت) |
تعداد دورها | عملیاتها | امنیت(در بیت) درمقابل حمله تصادم | ظرفیت در مقابل حمله طولانی مدت |
عملکرد در Skylake (متوسط cpb) [56] | اولین انتشار | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| پیام های طولانی | ۸ بایت | ||||||||||
| MD5 (as reference) | 128 | 128 (4 × 32) | 512 | 64 | And, Xor, Rot, Add (mod 232), Or | ≤18 (collisions found)[57] | 0 | 4.99 | 55.00 | 1992 | |
| SHA-0 | 160 | 160 (5 × 32) | 512 | 80 | And, Xor, Rot, Add (mod 232), Or | <34 (collisions found) | 0 | ≈ SHA-1 | ≈ SHA-1 | 1993 | |
| SHA-1 | <63 (collisions found)[58] | 3.47 | 52.00 | 1995 | |||||||
| SHA-2 | SHA-224 SHA-256 | 224 256 | 256 (8 × 32) | 512 | 64 | And, Xor, Rot, Add (mod 232), Or, Shr | 112 128 | 32 0 | 7.62 7.63 | 84.50 85.25 | 2004 2001 |
| SHA-384 SHA-512 | 384 512 | 512 (8 × 64) | 1024 | 80 | And, Xor, Rot, Add (mod 264), Or, Shr | 192 256 | 128 (≤ 384) 0 | 5.12 5.06 | 135.75 135.50 | 2001 | |
| SHA-512/224 SHA-512/256 | 224 256 | 112 128 | 288 256 | ≈ SHA-384 | ≈ SHA-384 | 2012 | |||||
| SHA-3 | SHA3-224 SHA3-256 SHA3-384 SHA3-512 | 224 256 384 512 | 1600 (5 × 5 × 64) | 1152 1088 832 576 | 24[59] | And, Xor, Rot, Not | 112 128 192 256 | 448 512 768 1024 | 8.12 8.59 11.06 15.88 | 154.25 155.50 164.00 164.00 | 2015 |
| SHAKE128 SHAKE256 | d (arbitrary) d (arbitrary) | 1344 1088 | min(d/2, 128) min(d/2, 256) | 256 512 | 7.08 8.59 | 155.25 155.50 | |||||
پیادهسازیها
در زیر لیستی از کتابخانههای رمزنگاری که از اساچای۳ پشتیبانی میکنند آمدهاست:
- sha3 Rust's
- Botan
- Bouncy Castle
- ++Crypto
- Libgcrypt
- Nettle
- OpenSSL
- wolfSSL
- MIRACL Cryptographic SDK
- Golang's x/crypto/sha3
استفاده در پروتکلها
- Ethereum#Ether § See also
جستارهای وابسته
- Ethash - یکی دیگر از درهمسازیهای مبتنیبر کچاک
منابع
- Morawiecki, Paweł; Pieprzyk, Josef; Srebrny, Marian (2013). Moriai, S, ed. "Rotational Cryptanalysis of Round-Reduced Keccak" (PDF). Fast Software Encryption Lecture Notes in Computer Science. Lecture Notes in Computer Science (به English). 8424: 241–262. doi:10.1007/978-3-662-43933-3_13. ISBN 978-3-662-43932-6. Archived from the original (PDF) on 2013-01-08. Retrieved 2019-02-08.
- Bertoni, Guido; Daemen, Joan; Peeters, Michaël; van Assche, Giles (January 14, 2011). "The Keccak SHA-3 submission" (PDF). keccak.noekeon.org. Archived from the original (PDF) on August 19, 2011. Retrieved February 9, 2014.
- Hernandez, Paul (2015-08-05). "NIST Releases SHA-3 Cryptographic Hash Standard". NIST.
- Dworkin, Morris J. (2015-08-04). "SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions". Federal Inf. Process. STDS. (NIST FIPS) – 202.
- "NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition". NIST. 2012-10-02. Retrieved 2012-10-02.
- Cruz, José R.C. (2013-05-07). "Keccak: The New SHA-3 Encryption Standard". Dr. Dobbs.
- Guido Bertoni; Joan Daemen; Michaël Peeters; Gilles Van Assche. "The Keccak sponge function family: Specifications summary". Retrieved 2011-05-11.
- "Third-Round Report of the SHA-3 Cryptographic Hash Algorithm Competition" (PDF). November 2012. doi:10.6028/NIST.IR.7896. Retrieved 2020-02-29. Sections 5.1.2.1 (mentioning "tree mode"), 6.2 ("other features", mentioning authenticated encryption), and 7 (saying "extras" may be standardized in the future).
- Bertoni, Guido; Daemen, Joan; Peeters, Michaël; Van Assche, Gilles; Van Keer, Ronny (2014-03-13). "CAESAR submission: Ketje v1" (PDF). Retrieved 2020-02-29.
- Bertoni, Guido; Daemen, Joan; Peeters, Michaël; Van Assche, Gilles; Van Keer, Ronny (2014-03-13). "CAESAR submission: Keyak v1" (PDF). Retrieved 2020-02-29.
- Guido Bertoni, Joan Daemen, Michaël Peeters and Gilles Van Assche. "Sponge Functions". Ecrypt Hash Workshop 2007.
- "Announcing Request for Candidate Algorithm Nominations for a New Cryptographic Hash Algorithm (SHA-3) Family [U.S. Federal Register Vol. 72 No. 212)]" (PDF). November 2, 2007. Archived from the original (PDF) on March 31, 2011. Retrieved July 18, 2017.
- Bertoni, Guido; Daemen, Joan; Peeters, Michaël; Van Assche, Gilles. "The road from Panama to Keccak via RadioGatún" (PDF). Retrieved 2020-02-29.
- KeccakReferenceAndOptimized-3.2.zip mainReference.c "The Keccak sponge function, designed by Guido Bertoni, Joan Daemen, Michaël Peeters and Gilles Van Assche. For more information, feedback or questions, please refer to our website: http://keccak.noekeon.org/Implementation%5Bپیوند+مرده%5D by the designers, hereby denoted as "the implementer". To the extent possible under law, the implementer has waived all copyright and related or neighboring rights to the source code in this file. https://creativecommons.org/publicdomain/zero/1.0/"
- Stevens, Marc; Bursztein, Elie; Karpman, Pierre; Albertini, Ange; Markov, Yarik. "The first collision for full SHA-1" (PDF). Archived from the original (PDF) on 15 May 2018. Retrieved 2017-02-23.
- Leurent, Gaëtan; Peyrin, Thomas. "SHA-1 is a Shambles". Retrieved 8 January 2020.
- "NIST Computer Security Division – The SHA-3 Cryptographic Hash Algorithm Competition, November 2007 – October 2012". 2017-01-04.
- "Keccak parameter changes for round 2". Keccak Team. 2009-09-22. Archived from the original on 2017-11-13. Retrieved 2020-02-29.
- "Simplifying Keccak's padding rule for round 3". Keccak Team. 2011-01-17. Retrieved 2020-02-29.
- "SHA-3 standardization". NIST. Retrieved 2015-04-16.
- National Institute of Standards and Technology (2015-08-05). "Federal Information Processing Standards: Permutation-Based Hash and Extendable-Output Functions, etc". Retrieved 2015-08-05.
- "Announcing Approval of Federal Information Processing Standard (FIPS) 202, SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions, and Revision of the Applicability Clause of FIPS 180-4, Secure Hash Standard". 2015-08-05.
- NIST (August 2015). "SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions" (PDF). doi:10.6028/NIST.FIPS.202. Retrieved 2020-02-29.
- "about 41 cycles/byte [...] represents a 40% speedup compared to an implementation using only 32-bit instructions". By formula we obtain
- Bertoni, Guido (2012-05-29). Keccak implementation overview (PDF). p. 25. Retrieved 2018-11-03.
- Bernstein, Daniel J. (2012-01-04). "Optimization failures in SHA-3 software" (PDF). cr.yp.to. Retrieved 2020-02-29.
- "Keccak Team". keccak.noekeon.org.
- Guo, Xu; Huang, Sinan; Nazhandali, Leyla; Schaumont, Patrick (Aug 2010), "Fair and Comprehensive Performance Evaluation of 14 Second Round SHA-3 ASIC Implementations" (PDF), NIST 2nd SHA-3 Candidate Conference: 12, retrieved 2011-02-18 Keccak is second only to Luffa, which did not advance to the final round.
- ARM corporation, ARM architecture reference manual ARMv8, for ARMv8-A architecture profile, document ARM DDI 0487C.a (ID121917), https://www.arm.com
- "Sakura: A Flexible Coding for Tree Hashing" (PDF). Keccak Team. 2014. Retrieved 2020-02-29.
- SHA-3 Derived Functions: cSHAKE, KMAC, TupleHash and ParallelHash
 This article incorporates text from this source, which is in the مالکیت عمومی.
This article incorporates text from this source, which is in the مالکیت عمومی. - "Keccak Team: KangarooTwelve". Keccak Team.
- "KangarooTwelve: fast hashing based on Keccak-p" (PDF). International Association for Cryptologic Research. 2016.
- "KangarooTwelve slides presented at ACNS 2018" (PDF). Keccak Team.
- "draft-irtf-cfrg-kangarootwelve-00 - KangarooTwelve". datatracker.ietf.org. IETF. Retrieved 2020-01-17.
- Guido Bertoni, Joan Daemen, Seth Hoffert, Michaël Peeters, Gilles Van Assche, Ronny Van Keer. "Farfalle: parallel permutation-based cryptography".
- Guido Bertoni, Joan Daemen, Seth Hoffert, Michaël Peeters, Gilles Van Assche, Ronny Van Keer. "The authenticated encryption schemes Kravatte-SANE and Kravatte-SANSE".
- "Abstract" (PDF). cr.yp.to.
- Brassard, Gilles; Høyer, Peter; Tapp, Alain (1998). "Quantum cryptanalysis of hash and claw-free functions". Abstract. Lecture Notes in Computer Science. 1380. pp. 163–169. arXiv:quant-ph/9705002. doi:10.1007/BFb0054319. ISBN 978-3-540-64275-6.
- "Cost Analysis" (PDF). cr.yp.to.
- "Collision problem" (PDF). scottaaronson.com.
- "Paper" (PDF). eprint.iacr.org. 2016.
- "Abstract" (PDF). eprint.iacr.org. 2017.
- John Kelsey. "SHA3, Where We've Been, Where We're Going" (PDF). RSA Conference 2013.
- John Kelsey. "SHA3, Past, Present, and Future". CHES 2013.
- "NIST hash forum mailing list". 2017-01-04.
- "The Keccak SHA-3 submission" (PDF). 2011-01-14. Retrieved 2014-02-08.
- "On 128-bit security".
- "A concrete proposal". 2013-10-02.
- "Schneier on Security: Will Keccak = SHA-3?".
- "LShift: Why I support the US Government making a cryptography standard weaker".
- "Yes, this is Keccak!".
- "Moving Forward with SHA-3" (PDF).
- NIST Computer Security Division (CSD). "SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions" (PDF). NIST.
- "NIST.gov – Computer Security Division – Computer Security Resource Center". 2016-12-29.
- "Measurements table". bench.cr.yp.to.
- Tao, Xie; Liu, Fanbao; Feng, Dengguo (2013). Fast Collision Attack on MD5 (PDF). Cryptology ePrint Archive (Technical report). IACR.
- Stevens, Marc; Bursztein, Elie; Karpman, Pierre; Albertini, Ange; Markov, Yarik. The first collision for full SHA-1 (PDF) (Technical report). Google Research. Lay summary – Google Security Blog (February 23, 2017).
- "The Keccak sponge function family". Retrieved 2016-01-27.