ثبات تغییر بازخورد خطی

شیفت‌رِجیستر فیدبک‌دار خطی (به انگلیسی: Linear feedback shift register) یا LFSR، شیفت‌رجیستری ${\displaystyle n}$-بیتی است که ترکیب خطی برخی از بیت‌های آن، به عنوان ورودی، به آن بازخورد (فیدبک) می‌شود (شکل روبرو را ببینید).

LFSR فیبوناچی چهاربیتی (راست)، و 15 حالت آن (چپ). خروجی گیت XOR، بازخورد را فراهم می‌کند. چندجمله‌ای متناظر این LFSR چنین است: ${\displaystyle p(x)=x^{4}+x^{3}+1\,}$. این LFSR پانزده حالت (state) دارد، زیرا چندجمله‌ای متناظر این LFSR، اول است، بنابراین ${\displaystyle 2^{4}-1=15}$.

کار LFSR با یک مقدار اولیۀ ${\displaystyle n}$-بیتی غیرصفر آغاز می‌شود. این مقدار اولیه، دانه (Seed) یا حالت اولیه (Initial state) نام دارد. رشته‌بیت‌های تولیدشدۀ LFSR، به حالت (State) کنونی و ورودی شیفت‌رجیستر بستگی دارد. چون تعداد حالات ممکن شیفت‌رجیستر، محدود است، رشته‌بیت خروجی آن تکرار می‌شود.

با انتخاب سرهای (بیت‌های) مناسب که ترکیب خطی آن‌ها به ورودی شیفت‌رجیستر بازخورد (فیدبک) می‌شود، می‌توان رشته‌ای از بیت‌ها را تولید کرد که شبه تصادفی (Pseudorandom) و دارای دوره تکرار طولانی هستند. اینکه کدام بیت‌های شیفت‌رجیستر برای فیدبک انتخاب شوند را چندجمله‌ای متناظر LFSR تعیین می‌کند. هر LFSR، یک چندجمله‌ای متناظر دارد.

در یک LFSR با شیفت‌رجیستر ${\displaystyle n}$-بیتی، حداکثر دورۀ تناوب رشته‌بیت تولیدشده، برابر ${\displaystyle 2^{n}-1\,}$ است. این مقدار به شرطی به‌دست می‌آید که چندجمله‌ای متناظر LFSR، اول (primitive) باشد. چندجمله‌ای اول، کاهش‌ناپذیر (irreducible) است، یعنی نمی‌توان آن‌را به عوامل اول تجزیه کرد. در این حالت، رشته‌بیت تولیدشده را «رشتۀ با طول بیشینه» (maximum-length sequence) یا به اختصار m-رشته (m-sequence) می‌گویند. m-رشته‌ها، خواص جالبی دارند؛ مثلاً اینکه تابع خودهمبستگی آن‌ها، شباهت زیادی به تابع خودهمبستگی نویز سفید دارد، و نیز اینکه، تعداد صفر و یک‌ها در آن‌ها، تقریباً برابر است. به این دو دلیل، آن‌ها شبه تصادفی هستند.

اصول عملکرد LFSRها، در مبحث میدان‌های محدود (Finite fields) در ریاضیات مطرح می‌شود. میدان‌های محدود را با${\displaystyle F_{q^{n}}}$ نشان می‌دهند، که ${\displaystyle q\,}$، عددی اول و ${\displaystyle n}$ عددی طبیعی است (در اینجا، طول شیفت‌رجیستر). اعضای ${\displaystyle F_{q^{n}}}$، چندجمله‌ای‌هایی هستند که درجۀ آن‌ها، حداکثر برابر ${\displaystyle n}$ است، و ضرائب آن‌ها از مجموعۀ ${\displaystyle F_{q}=\{0,1,2,\dots ,q-1\}}$ گرفته می‌شوند. چندجمله‌ای متناظر LFSR، در این میدان تعریف می‌شود. اگر ${\displaystyle q=2}$ باشد، خروجی LFSR، یک رشته‌بیت (باینری) است.

نام دیگر میدان‌های محدود، میدان‌های گالوا (Galois fields) است؛ به افتخار ریاضی‌دان فرانسوی، اِواریست گالوا (Evariste Galois).

کاربردی از LFSR در تولید اعداد شبه تصادفی (تولید نویز سفید) است. در مهندسی برق (به ویژه مخابرات) و کامپیوتر از LFSRها استفاده می‌شود.

پیاده‌سازی LFSR به روش فیبوناچی (Fibonacci)

یک LFSR شانزده‌بیتی فیبوناچی، بیت‌های بازخورد را چندجمله‌ای اول (primitive) تعیین می‌کند، بنابراین دورۀ تناوب رشتۀ خروجی ۶۵۵۳۵ است.

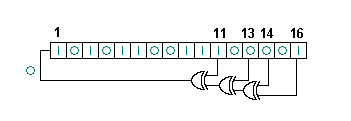
در یک LFSR، سرهای شیفت‌رجیستر که ترکیب خطی بیت‌های متناظر آن‌ها، به شیفت‌رجیستر فیدبک می‌شود، تَپ (tap) نام دارند. مثلاً در شکل روبرو، این تپ‌ها [۱۶٬۱۴٬۱۳٬۱۱] هستند.

بنابراین، چندجمله‌ای متناظر LFSR در این مثال چنین است:

${\displaystyle p(x)=x^{16}+x^{14}+x^{13}+x^{11}+1}$

که یک چندجمله‌ای اول (primitive) دودویی (باینری) است، به این معنی که ضرائب چندجمله‌ای، صفر یا یک هستند. بیت‌های متناظر با این تپ‌ها، با هم XOR (یای انحصاری) شده، و حاصل وارد شیفت‌رجیستر می‌شود (فیدبک می‌شود). بیت شانزدهم، خروجی LFSR نیز هست.

دورۀ تناوب رشته‌بیت تولیدشده این LFSR، ${\displaystyle 2^{n}-1=2^{16}-1=65535}$است.

مثالی از کد به زبان C برای تولید این LFSR چنین است؛

# include <stdint.h>
uint16_t lfsr = 0xACE1u;
unsigned bit;
unsigned period = ۰;
do {
  /* taps: 16 14 13 11; feedback polynomial: x^16 + x^14 + x^13 + x^11 + 1 */
  bit  = ((lfsr>> 0) ^ (lfsr>> 2) ^ (lfsr>> 3) ^ (lfsr>> 5)) & ۱;
  lfsr =  (lfsr>> 1) | (bit <<15);
  ++period;
} while(lfsr!= 0xACE1u);

مقدار (حالت) اولیۀ این LFSR، عدد ${\displaystyle {\texttt {0xACE1u}}}$است که در مبنای شانزده نوشته شده‌است.

پیاده‌سازی LFSR به روش گالوا (Galois)

یک LFSR گالوا ۱۶بیتی.

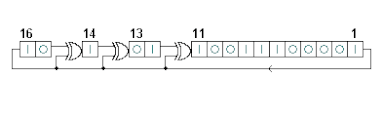
LFSR گالوا، ساختار دیگری برای پیاده‌سازی LFSRها است (شکل روبرو).

نمونه کد به زبان C برای پیاده‌سازی یک LFSR گالوا با یک شیفت‌رجیستر 32-بیتی در زیر آمده است:

# include <stdint.h>
uint32_t lfsr = ۱;
unsigned period = ۰;

do {
  /* taps: 32 31 29 1; feedback polynomial: x^32 + x^31 + x^29 + x + 1 */
  lfsr = (lfsr>> 1) ^ (-(lfsr & 1u) & 0xD0000001u);
  ++period;
} while(lfsr!= 1u);

و کد نمونه ۱۶ بیتی در شکل، چنین است:

# include <stdint.h>
uint16_t lfsr = 0xACE1u;
unsigned period = ۰;

do {
  /* taps: 16 14 13 11; feedback polynomial: x^16 + x^14 + x^13 + x^11 + 1 */
  lfsr = (lfsr>> 1) ^ (-(lfsr & 1u) & 0xB400u);
  ++period;
} while(lfsr!= 0xACE1u);

# include <stdint.h>
uint16_t lfsr = 0xACE1u;
unsigned period = ۰;

do {
  unsigned lsb = lfsr & 1;  /* Get lsb (i.e.، the output bit). */
  lfsr>>= 1;               /* Shift register */
  if (lsb == 1)             /* Only apply toggle mask if output bit is 1. */
    lfsr ^= 0xB400u;        /* Apply toggle mask, value has 1 at bits corresponding
                             * to taps, 0 elsewhere. */
  ++period;
} while(lfsr!= 0xACE1u);

LFSR با خروجی غیر دودویی (non binary)

اگر ${\displaystyle q>2}$ باشد، رشتۀ خروجی LFSR، از اعداد مجموعۀ ${\displaystyle \{0,1,2,\dots q-1\}}$ تشکیل می‌شود. در حالت خاص ${\displaystyle q=2}$، خروجی LFSR، رشته‌ای از بیت‌هاست.

برخی چندجمله‌ای‌های اول (primitive)

اینجا[1][2]، برخی از چندجمله‌ای‌های اول دارای طول ماکسیمم (m-رشته) برای ${\displaystyle 2\geq n\leq 32\,}$ لیست شده‌اند.

1. «Pseudo-Random Number Generation Routine for the MAX765x Microprocessor - Application Note - Maxim». www.maximintegrated.com. دریافت‌شده در ۲۰۱۹-۰۳-۲۰.
2. «A Linear Feedback Shift Register is a sequential shift register with combinational logic that causes it to pseudo-randomly cycle through a sequence of binary values». www.ece.ualberta.ca. دریافت‌شده در ۲۰۱۹-۰۳-۲۰.

• International Telecommunications Union Recommendation O.151 (August 1992)
• Maximal Length LFSR table with length from 2 to 67. (Error detected: period are (2^n)-1 not 2^n)
• Pseudo-Random Number Generation Routine
• http://www.quadibloc.com/crypto/co040801.htm
• Feedback terms
• General LFSR Theory
• An implementation of LFSR in VHDL.

پیوند به بیرون