الگوریتم فلوید-وارشال

در علوم کامپیوتر الگوریتم فلوید-وارشال (به انگلیسی: Floyd–Warshall algorithm) یک الگوریتم تحلیل گراف برای پیدا کردن کوتاهترین مسیر در یک گراف جهت دار و وزن دار می‌باشد. با یکبار اجرای این الگوریتم کوتاه‌ترین مسیر بین همهٔ جفت راس‌ها پیدا خواهد شد. الگوریتم فلوید-وارشال به نام استفن وارشال و رابرت فلوید نامگذاری شده‌است. این الگوریتم یک مثال از برنامه‌نویسی پویا می‌باشد. در این الگوریتم، ابتدا ماتریس مجاورت برای نقاط گراف نوشته شده و در مرحلهٔ بعد با استفاده از یک راس واسطه، کوتاه‌ترین فاصله بین نقاط را محاسبه کرده و ماتریس را با مقادیر جدید بازنویسی می‌کند. پس از آن دو نقطه به عنوان واسطه انتخاب شده و ماتریس جدید به دست می‌آید. با تکرار این روند الگوریتم به پایان رسیده و در نهایت ماتریسی ایجاد شده که کوتاه‌ترین مسیر بین تمامی نقاط را محاسبه کرده‌است. بدیهی است که کوتاه‌ترین مسیر بین مبدأ و مقصد را می‌توان به راحتی از ماتریس تشکیل شده‌استخراج نمود.

الگوریتم فلوید-وارشال

رده	مسئله یافتن کوتاهترین مسیر (برای گراف‌های وزن‌دار)
ساختمان داده	گراف (ساختار داده)
کارایی بدترین حالت	${\displaystyle \Theta (|V|^{3})}$
کارایی بهترین حالت	${\displaystyle \Theta (|V|^{3})}$
کارایی متوسط	${\displaystyle \Theta (|V|^{3})}$
پیچیدگی فضایی	${\displaystyle \Theta (|V|^{2})}$

الگوریتم

الگوریتم وارشال همهٔ مسیرهای ممکن در یک گراف، بین هر جفت از راس هارا مقایسه می‌کند. این الگوریتم قادر است این کار را تنها با ${\displaystyle V^{3}}$ مقایسه انجام دهد. این ملاحظه قابل توجهی می‌باشد که در یک گراف ${\displaystyle V^{2}}$ یال وجود داشته باشد وهر ترکیبی از یالها چک شده باشد. یک گراف ${\displaystyle G}$ با راس‌های ${\displaystyle Vi}$ که i از ۱ تا N می‌باشد را در نظر بگیرید. علاوه بر این یک تابع به نام (shortestPath(i,j،k را در نظر بگیرید که کوتاهترین مسیر ممکن از i تا j را با استفاده از راس‌های ۱ تا k که به عنوان راسهای میانی در امتداد مسیر می‌باشند را برمی‌گرداند.

هم اکنون این تابع داده شده‌است. هدف ما پیدا کردن کوتاهترین مسیر از هر i تا هر j تنها با استفاده از راسهای ۱ تا 1+k می‌باشد. دو کاندیدا برای این مسیر وجود دارد:

۱- کوتاهترین مسیری که فقط از راس‌های موجود در مجموعه ی(k,........ ,1) استفاده می‌کند.

۲- تعدادی مسیر که از i تا 1+k و سپس از 1+k تا j می‌روند وجود دارد که این مسیر بهتر می‌باشد.

ما می‌دانیم که بهترین مسیر از i تا j که فقط از راس‌های بین ۱ تا k+1 استفاده می‌کند توسط (ShortestPath(i,j،k تعریف شده‌است و واضح است که اگر یک مسیر بهتر از i تا1+k و از 1+k تا j وجود داشته باشد بنابراین طول مسیر بین i,j از الحاق کوتاهترین مسیر از i تا 1+k و کوتاهترین مسیر از 1+k تا j بدست می‌آید؛ بنابراین تابع (ShortestPath(i,j،k را در در فرمول بازگشتی زیر ارائه می‌دهیم:

${\displaystyle {\textrm {shortestPath}}(i,j,k)=\min({\textrm {shortestPath}}(i,j,k-1),{\textrm {shortestPath}}(i,k,k-1)\,+\,{\textrm {shortestPath}}(k,j,k-1));\,\!}$

این رابطه قلب الگوریتم وارشال می‌باشد این الگوریتم در اولین محاسبه (ShortestPath(i,j،۱ را برای همهٔ جفت‌های (i ,j) پیدا می‌کند و سپس از این برای پیدا کردن (Shortestpath(i,j،۲ برای همهٔ جفت‌های (i ,j) استفاده می‌شود و این روال تا زمانی که k=N شود ادامه می‌یابد و ما می‌توانیم کوتاهترین مسیر بین جفت‌های (i,j) را با استفاده از راس‌های میانی پیدا کنیم.

شبه کد

1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
2 for each edge (u,v)
3    dist[u][v] ← w(u,v)  // the weight of the edge (u,v)
4 for each vertex v
5    dist[v][v] ← 0
6 for k from 1 to |V|
7    for i from 1 to |V|
8       for j from 1 to |V|
9          if dist[i][j] > dist[i][k] + dist[k][j] 
10             dist[i][j] ← dist[i][k] + dist[k][j]
11         end if

تحلیل

در هر مرحله‌ی برای یافتن تمامی ${\displaystyle n^{2}}$ مقدار ${\displaystyle {\textrm {shortestPath}}(i,j,k)}$‌ها (برای ${\displaystyle k}$های بزرگ‌تر از ۰ و تمامی ${\displaystyle i,j}$ها) با استفاده از مقادیر ${\displaystyle {\textrm {shortestPath}}(i,j,k-1)}$ نیاز به ${\displaystyle 2n^{2}}$ عملیات داریم. با توجه به این که ما با مقداردهی اولیه ${\displaystyle \mathrm {shortestPath} (i,j,0)=\mathrm {edgeCost} (i,j)}$ شروع می‌کنیم و سپس دنباله‌ٔ

${\displaystyle n}$ ${\displaystyle \mathrm {shortestPath} (i,j,1)}$, ${\displaystyle \mathrm {shortestPath} (i,j,2)}$, ${\displaystyle \ldots }$, ${\displaystyle \mathrm {shortestPath} (i,j,n)}$

را محاسبه می‌کنیم، مجموع تعداد عملیات‌های مورد نیاز ما برابر با ${\displaystyle n\cdot 2n^{2}=2n^{3}}$ خواهد بود. در نتیجه پیجدگی محاسباتی این الگوریتم از ${\displaystyle \Theta (n^{3})}$ خواهد بود.

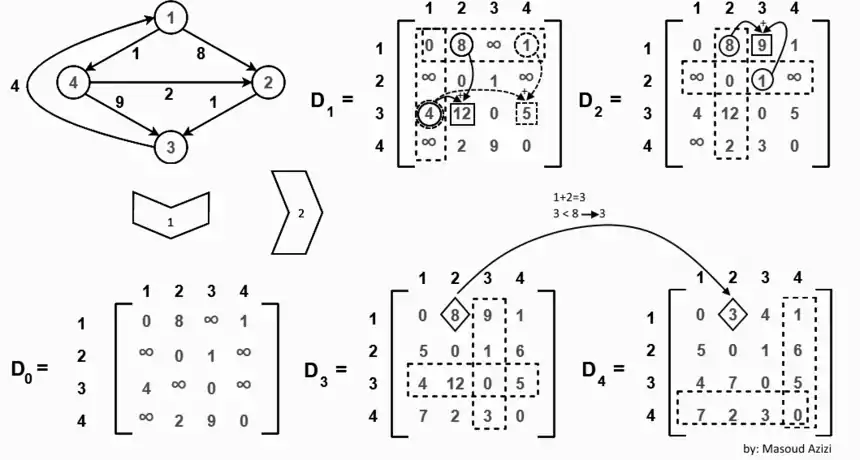
تحلیل دستی با یک مثال

در این تصویر مشاهده میکنید که چگونه توسط استخراج ماتریس مجاورت(D0) از گراف روابط وزن دار الگوریتم فلوید وارشال را به صورت دستی در چهار مرحله اعمال کرده ایم.

تحلیل دستی الگوریتم فلوید وارشال

کاربردها

الگوریتم وارشال برای حل مسایل زیر می‌تواند استفاده شود.

1. کوتاهترین مسیرها در گراف‌های جهت دار
2. بستار متعدی گراف‌های جهت دار
3. در فرمول عمومی الگوریتم وارشال گراف بی وزن می‌باشد و توسط یک ماتریس مجاورت نمایش داده شده‌است.
4. وارون سازی یک ماتریس حقیقی
5. تست کردن اینکه آیا یک گراف بی جهت، دو قسمتی می‌باشد یا خیر.
6. محاسبه سریع شبکه‌های راه‌یاب

پیاده‌سازی‌ها

پیاده‌سازی این الگوریتم در زبان‌های برنامه‌نویسی مختلفی وجود دارد.

1. برای پرل در کتابخانه Graph
2. برای جاوااسکریپت در کتابخانه Cytoscape
3. برای سی پلاس‌پلاس در کتابخانه boost::graph
4. برای سی شارپ در کتابخانه QuickGraph
5. برای جاوا در کتابخانه Apache Commons Graph

۶- برای متلب در بسته Matlab_bgl

۷- برای پایتون در کتابخانه SciPy یا کتابخانه NetworkX

۸- برای R در کتابخانه e1071

منابع

• مقدمه‌ای بر الگوریتم‌ها - پدیدآورنده: تامس کورمن، چارلز لیزرسان، رونالد دیوست، کلیفورد اشتاین - گروه مهندسی-پژوهشی خوارزمی (مترجم) - ناشر: درخشش
• ویکی‌پدیای انگلیسی