برنامه‌نویسی پویا

در علوم رایانه و ریاضیات، برنامه‌ریزی پویا یا داینامیک روشی کارآمد برای حل مسائل جستجو و بهینه‌سازی با استفاده از دو ویژگی زیرمسئله‌های هم‌پوشان و زیرساخت‌های بهینه است. بر خلاف برنامه‌ریزی خطی، چارچوب استانداردی برای فرموله کردن مسائل برنامه‌ریزی پویا وجود ندارد. در واقع، آنچه برنامه‌ریزی پویا انجام می‌دهد ارائه روش برخورد کلی جهت حل این نوع مسائل است. در هر مورد، باید معادلات و روابط ریاضی مخصوصی که با شرایط آن مسئله تطبیق دارد نوشته شود.[1]

تاریخچه

این روش در سال ۱۹۵۳ توسط ریاضی‌دانی به نام ریچارد بلمن معرفی شد. برنامه‌ریزِی پویا در ریاضی و علوم رایانه روشی شناخته شده‌است که از آن در نوشتن الگوریتم‌های بهینه با استفاده از حذف اجرای چند بارهٔ یک زیر مسئله یکسان استفاده می‌شود. تعریف برنامه‌ریزی پویا در ریاضی و علوم رایانه متفاوت است. نشان داده شده‌است که روش علوم رایانه‌ای برای برنامه‌ریزی پویا کارایی بالاتری دارد زیرا محاسبات تکراری را حذف می‌کند در حالی که در روش ریاضی برنامه‌ریزی پویا امکان کاهش فضای حافظه بیشتر است.

برنامه‌ریزی پویا شبیه روش تقسیم و حل، مسائل را با استفاده از ترکیب کردن جواب زیرمسئله‌ها حل می‌کند. الگوریتم تقسیم و حل، مسئله را به زیر مسئله‌های مستقل تقسیم می‌کند و پس از حل زیر مسئله‌ها به صورت بازگشتی، نتایج را با هم ترکیب کرده و جواب مسئله اصلی را بدست می‌آورد. به عبارت دقیق تر، برنامه‌ریزی پویا بهتر است در مسائلی استفاده شود که زیرمسئله‌ها مستقل نیستند؛ یعنی زمانی که زیرمسئله‌ها، خود دارای چندین زیر مسئلهٔ یکسان هستند. در این حالت روش تقسیم و حل با اجرای مکرر زیرمسئله‌های یکسان، بیشتر از میزان لازم محاسبات انجام می‌دهد. یک الگوریتم برنامه‌ریزی پویا زیرمسئله‌ها را یک بار حل و جواب آن‌ها را در یک جدول ذخیره می‌کند و با این کار از تکرار اجرای زیرمسئله‌ها در زمانی که مجدداً به جواب آن‌ها نیاز است جلوگیری می‌کند. مثلا اگر مسئله فیبوناچی با برنامه ریزی پویا حل شود باعث اجرای مکرر یک زیرمسئله نمی شود. مثلا برای محاسبه f(5) مقادیر f(4) و f(3) تنها یک بار محاسبه می شوند. ولی اگر از روش تقسیم و حل استفاده شود. f(3) دو بار محاسبه می شود که سربار محاسباتی است.

ویژگی‌ها

یک مسئله باید دارای دو مشخصهٔ کلیدی باشد تا بتوان برنامه‌نویسی پویا را برای آن به کار برد: زیرساختار بهینه و زیرمسئله‌های هم‌پوشان.[2] در طرف مقابل، به حل یک مسئله با ترکیب جواب‌های بهینهٔ زیرمسئله‌های ناهم‌پوشان، «تقسیم و حل» گفته‌می‌شود. به همین علت است که مرتب‌سازی ادغامی و سریع به عنوان مسائل برنامه‌نویسی پویا شناخته‌نمی‌شوند.

اصل بهینگی

اگر بنا باشد پرانتزبندی کل عبارت بهینه شود، پرانتزبندی زیرمسئله‌ها هم باید بهینه باشند. یعنی بهینه بودن مسئله، بهینه بودن زیرمسئله‌ها را ایجاب می‌کند. پس می‌توان از روش برنامه‌نویسی پویا استفاده کرد.

حل بهینه، سومین مرحله از بسط یک الگوریتم برنامه‌نویسی پویا برای مسائل بهینه‌سازی است. مراحل بسط چنین الگوریتمی به شرح زیر است:

1. ارائه یک ویژگی بازگشتی که حل بهینهٔ نمونه‌ای از مسئله را به دست می‌دهد.
2. محاسبه مقدار حل بهینه به شیوهٔ جزء به کل.
3. بنا کردن یک حل نمونه به شیوهٔ جزء به کل.

تمام مسائل بهینه‌سازی را نمی‌توان با برنامه‌نویسی پویا حل کرد چرا که باید اصل بهینگی در مسئله صدق کند.

اصل بهینگی در یک مسئله صدق می‌کند اگر یک حل بهینه برای نمونه ای از مسئله، همواره حاوی حل بهینه برای همهٔ زیر نمونه‌ها باشد.

در روش برنامه‌نویسی پویا اغلب از یک آرایه برای ذخیره نتایج جهت استفاده مجدد استفاده شده، و زیرمسائل به صورت جزء به کل حل می‌شوند. در مورد این مسئله، ابتدا زیرمسائلی که تنها از دو ماتریس تشکیل شده‌اند محاسبه می‌شوند. سپس زیرمسائلی که از سه ماتریس تشکیل شده‌اند محاسبه می‌شوند. این دسته از زیرمسائل به زیرمسائلی متشکل از دو ماتریس تجزیه می‌شوند که قبلاً محاسبات آن‌ها صورت گرفته، و نتایج آن‌ها در آرایه ذخیره شده‌اند. در نتیجه نیاز به محاسبه مجدد آن‌ها نیست. به همین ترتیب در مرحله بعد زیرمسائل با چهار ماتریس محاسبه می‌شوند، و الی آخر.

درختهای جستجوی دودویی بهینه

درخت جستجوی دودویی یک درخت دودویی از عناصر است که معمولاً کلید نامیده می‌شوند به قسمی که:

1. هر گره حاوی یک کلید است.
2. کلیدهای موجود در زیردرخت چپ هر گره، کوچکتر یا مساوی کلید آن گره هستند.
3. کلیدهای موجود در زیردرخت راست هر گره، بزرگتر یا مساوی کلید آن گره هستند

زیرسازه بهینه

زیرساختار بهینه به این معناست که جواب یک مسئلهٔ بهینه‌سازی را بتوان از ترکیب جواب‌های بهینهٔ زیرمسئله‌های آن به دست آورد. چنین زیرساختارهای بهینه‌ای معمولاً با رویکرد بازگشتی به دست می‌آیند؛ برای مثال، در گراف (G=(V,E، کوتاه‌ترین مسیرِ م از رأس آ به رأس ب، زیرساختار بهینه از خود نشان می‌دهد: هر رأس میانیِ ث از مسیرِ م را در نظر بگیرید. اگر م واقعاً کوتاه‌ترین مسیر باشد، آنگاه می‌توان آن را به دو زیرمسیر م_۱ از آ تا ث و م_۲ از ث تا ب در نظر گرفت، به نحوی که هر کدام از این‌ها کوتاه‌ترین مسیر بین دو سر خود هستند (به همان طریق برش و چسباندن کتاب مقدمه‌ای بر الگوریتم‌ها). بر این اساس، می‌توان جواب را به صورت بازگشتی بیان کرد، درست مانند الگوریتم‌های بلمن-فورد و فلوید-وارشال.[3]

استفاده از روش زیرسازه بهینه به این معناست که مسئله را به زیرمسئله‌هایی کوچک‌تر بشکنیم و برای هر یک از این زیرمسئله‌ها پاسخی بهینه بیابیم و پاسخ بهینه مسئلهٔ کلی را از کنار هم قرار دادن این پاسخ‌های بهینهٔ جزئی به دست آوریم. مثلاً در هنگام حل مسئلهٔ یافتن کوتاه‌ترین مسیر از یک رأس یک گراف به رأسی دیگر، می‌توانیم کوتاه‌ترین مسیر تا مقصد از همهٔ رئوس مجاور را به دست آوریم و از آن برای جواب کلی استفاده کنیم. به‌طور کلی حل مسئله از این روش شامل سه مرحله است.

1. شکستن مسئله به بخش‌های کوچک‌تر
2. حل خود این زیرمسئله‌ها با شکاندن آن‌ها به صورت بازگشتی
3. استفاده از پاسخ‌های جزئی برای یافتن پاسخ کلی

زیرمسئله‌های هم‌پوشان

زیرمسئله‌های هم‌پوشان به معنای کوچک بودن فضای زیرمسئله‌هاست، به این معنا که هر الگوریتم بازگشتی برای حل این مسئله، باید به جای ایجاد زیرمسئله‌های جدید، زیرمسئله‌های تکراری را بارها حل کند. برای مثال، به فرمول بازگشی دنبالهٔ فیبوناچی دقت کنید: F_i = F_i−1 + F_i−2، با حالات پایهٔ F₁ = F₂ = ۱. آنگاه F₄₃ = F₄₂ + F₄₁، و F₄₂ = F₄₁ + F₄₀. اکنون F₄₁ در زیردرخت‌های هر دوی F₄₃ و F₄₂ محاسبه می‌شود. در صورت اتخاذ چنین رویکرد ساده‌انگارانه‌ای، نهایتاً زیرمسئله‌های یکسانی را بارها حل می‌کنیم، در صورتی که تعداد کل زیرمسئله‌ها در واقعیت کم است (تنها ۴۳تا). برنامه‌نویسی پویا به این حقیقت دقت می‌کند و هر زیرمسئله را تنها یک بار حل می‌کند.[4]

گفته می‌شود مسئله‌ای دارای زیرمسئله‌های هم‌پوشان است، اگر بتوان مسئله را به زیرمسئله‌های کوچکتری شکست که پاسخ هرکدام چند بار در طول فرایند حل مورد استفاده قرار بگیرد.[5] برنامه‌ریزی پویا کمک می‌کند تا هر کدام از این پاسخ‌ها فقط یک بار محاسبه شوند و فرایند حل از بابت دوباره‌کاری هزینه‌ای را متحمل نشود. برای مثال در دنباله فیبوناچی برای محاسبهٔ عدد چهارم دنباله به دانستن عدد سوم نیاز داریم. برای محاسبهٔ عدد پنجم هم باز به عدد سوم نیاز داریم. حال اگر مثلاً در شرایطی بخواهیم عدد ششم دنبالهٔ فیبوناچی را حساب کنیم، در این محاسبه هم مقدار عدد پنجم را می‌خواهیم و هم مقدار عدد چهارم را. اگر تصمیم بگیریم اعداد چهارم و پنجم را به نوبت حساب کنیم در هنگام محاسبهٔ هرکدام به مقدار عدد سوم نیاز پیدا می‌کنیم و باید دوباره آن را محاسبه کنیم. برای جلوگیری از این محاسبات چندباره، الگوریتمهایی که مبتنی بر برنامه‌ریزی پویا هستند، معمولاً یکی از دو راه زیر را استفاده می‌کنند.

• رویکرد بالا به پایین: راه درروی مستقیم از صورت‌بندی بازگشتی هر مسئله‌ای است. اگر جواب مسئله‌ای را بتوان به صورت بازگشتی با جواب زیرمسئله‌های آن به دست آورد، و در صورت هم‌پوشانی زیرمسئله‌ها، می‌توان جواب زیرمسئله‌ها را در یک جدول به خاطر سپرد. هر گاه که برای حل یک زیرمسئله اقدام می‌کنیم، ابتدا بررسی می‌کنیم که آیا این زیرمسئله قبلاً حل شده یا نه؛ اگر جواب آن را داشتیم، می‌توانیم آن را مستقیماً استفاده کنیم؛ در غیر این صورت، زیرمسئله را حل می‌کنیم و جواب آن را به جدول اضافه می‌کنیم. در این رویکرد مسئله به زیرمسئله‌هایی شکسته می‌شود و پاسخ هر زیرمسئله پس از محاسبه در جایی ذخیره می‌شود. در مراحل بعدی هر وقت به آن پاسخ نیاز بود پاسخ از روی حافظه خوانده می‌شود. این فرایند ترکیبی از الگوریتم بازگشتی و ذخیره‌سازی در حافظه است.
• رویکرد پایین به بالا: پس از آن که جواب یک مسئله را به صورت بازگشتی با استفاده از زیرمسئله‌های آن صورت‌بندی کردیم، می‌توانیم مسئله را از پایین به بالا نگاه کنیم: ابتدا زیرمسئله‌ها را حل می‌کنیم و سپس جواب آن‌ها را برای به دست آوردن جواب زیرمسئله‌های بزرگ‌تر استفاده می‌کنیم تا نهایتاً به مسئلهٔ اصلی برسیم. این روش نیز معمولاً به کمک یک جدول با تولید مرحله به مرحلهٔ زیرمسئله‌های بزرگ‌تر و بزرگ‌تر به کمک جواب زیرمسئله‌های کوچک‌تر انجام می‌شود؛ برای مثال، اگر مقادیر F₄₁ و F₄₀ را بدانیم، می‌توانیم مستقیماً مقدار F₄₂ را به دست آوریم. در این رویکرد همهٔ زیرمسئله‌های مورد نیاز از کوچک به بزرگ حل می‌شوند و از جواب‌ها «بلافاصله» برای محاسبهٔ بعدی‌ها استفاده می‌شود و فرایند محاسبه تا رسیدن به زیرمسئلهٔ مورد نیاز (که در واقع مسئلهٔ اصلی ماست) ادامه می‌یابد. بدیهی است که در این حالت استفاده از الگوریتم بازگشتی ضروری نیست. مثال زیر این تفاوت‌ها را روشن‌تر می‌کند. برخی از زبان‌های برنامه‌نویسی می‌توانند به‌طور خودکار جواب صدا زدن یک تابع با ورودی‌های مشخص را به خاطر بسپارند تا صدا زدن با نام را سرعت ببخشند (این فرایند با نام صدا زدن با نیاز شناخته‌می‌شود). برخی زبان‌ها به شکل سیار این امکان را در اختیار برنامه‌نویس قرار می‌دهند (مانند Scheme ,Common Lisp ,[6]Perl و D). برخی زبان‌های نیز به صورت خودکار به‌خاطرسپاری را در خود دارند: مانند Prolog جدول‌دار و J، که به‌خاطرسپاری را با قید .M پشتیبانی می‌کند.[7] در هر صورت، این تنها برای یک تابع با شفافیت ارجاعی امکان دارد. به‌خاطرسپاری به عنوان یک الگوی طراحی در دسترس نیز در زبان‌های بازنویسی جملات مانند زبان ولفرام یافت‌می‌شود.

گراف زیرمسئله‌ها

تصویر ۱. گراف زیرمسئله‌های دنبالهٔ فیبوناچی. درخت نبودن این گراف نشان‌دهندهٔ زیرمسئله‌های هم‌پوشان است.

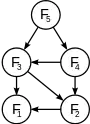
زمانی که به یک مسئلهٔ برنامه‌نویسی پویا می‌اندیشیم، باید مجموعهٔ زیرمسئله‌های موجود و چگونگی وابستگی آن‌ها را درک کنیم.

گراف زیرمسئله‌ها دقیقاً همین اطلاعات را برای یک مسئله در بر می‌گیرد. تصویر ۱ گراف زیرمسئله‌های دنباله‌های فیبوناچی را نشان می‌دهد. گراف زیرمسئله‌ها یک گراف جهت‌دار، شامل یک رأس به ازای هر زیرمسئلهٔ متمایز است و در صورتی یک یال جهت‌دار از رأس زیرمسئلهٔ x به رأس زیرمسئلهٔ y دارد که برای تعیین یک جواب بهینه برای زیرمسئلهٔ x مستقیماً نیاز به در نظر گرفتن یک جواب بهینه برای زیرمسئلهٔ y داشته‌باشیم. برای نمونه، گراف زیرمسئله دارای یک یال از x به y است، در صورتی که یک رویهٔ (procedure) بازگشتی بالا به پایین برای حل x، مستقیماً خود را برای حل y صدا بزند. می‌توان گراف زیرمسئله‌ها را یک نسخهٔ کاهش‌یافتهٔ درخت بازگشتی برای روش بازگشتی بالا به پایین در نظر گرفت، به گونه‌ای که همهٔ رئوس مربوط به یک زیرمسئله را یکی کنیم و یال‌ها را از والد به فرزند جهت‌دار کنیم.

روش پایین به بالا برای برنامه‌نویسی پویا رئوس گراف زیرمسئله‌ها را به ترتیبی در نظر می‌گیرد که همهٔ زیرمسئله‌های مجاور یک زیرمسئله، پیش از آن حل شوند. در یک الگوریتم برنامه‌نویسی پویای پایین به بالا، رئوس گراف زیرمسئله‌ها را به صورتی در نظر می‌گیریم که «معکوس مرتب توپولوژیکی» یا «مرتب توپولوژیک وارون» زیرگراف مسئه‌ها است. به زبان دیگر، هیچ زیرمسئله‌ای تا زمانی که همهٔ زیرمسئله‌هایی که به آن‌ها وابسته است حل نشده‌اند، در نظر گرفته‌نمی‌شود. به‌طور مشابه، می‌توانیم رویکرد بالا به پایین (همراه به‌خاطرسپاری) برای برنامه‌نویسی پویا را به شکل جستجوی ژرفانخست گراف زیرمسئله‌ها ببینیم.

اندازهٔ گراف زیرمسئله‌ها می‌تواند ما را در تعیین زمان اجرای الگوریتم برنامه‌نویسی پویا یاری کند. از آنجایی که هر زیرمسئله را فقط یک بار حل می‌کنیم، زمان اجرا برابر است با مجموع تعداد بارهایی که نیاز است هر زیرمسئله را حل کنیم. به‌طور معمول، زمان محاسبهٔ جواب یک زیرمسئله، متناسب با درجهٔ رأس متناظر در گراف، و تعداد زیرمسئله‌ها برابر با تعداد رئوس گراف است.[8]

مثال

یک پیاده‌سازی ساده از یک تابع برای یافتن عدد فیبوناچی nام می‌تواند به شکل زیر باشد.

function fib(n)
    if n = 0    
        return 0        
    if n = 1    
        return 1        
    return fib(n − 1) + fib(n − 2)  

برای مثال اگر از چنین تابعی (fib(5 را بخواهیم، تابع‌هایی که صدا می‌شوند به شکل زیر خواهند بود.

1. fib(5)
2. fib(4) + fib(3)
3. (fib(3) + fib(2)) + (fib(2) + fib(1))
4. ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
5. (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))

مشخص است که چنین فرایندی پر از محاسبات تکراری است. مثلاً عدد فیبوناچی دوم به تنهایی سه بار حساب شده‌است. در محاسبات بزرگ‌تر چنین تکرارهایی برنامه را به شدت کند می‌کنند. این الگوریتم دارای پیچیدگی زمانی نمایی است. حال فرض کنید ما یک آرایه دوتایی map داریم که عدد n را به مقدار عدد فیبوناچی nام مربوط کرده و ذخیره می‌کند. پیچیدگی زمانی چنین الگوریتمی n خواهد بود. همچنین میزان فضای اشغال‌شده‌اش هم از مرتبه n خواهد بود.

var m := map(0 → 1, 1 → 1)
function fib(n)
    if map m does not contain key n
        m[n] := fib(n − 1) + fib(n − 2)
    return m[n]

این نمونه‌ای از فرایند بالا به پایین بود. چون ابتدا مسئله را شکستیم و بعد به محاسبه و ذخیرهٔ پاسخ زیرمسئله‌ها پرداختیم.

در فرایند پایین به بالا برای حل چنین مسئله‌ای از عدد فیبوناچی یکم شروع می‌کنیم تا به عدد خواسته‌شده برسیم. با این کار باز هم پیچیدگی زمانی از مرتبه n است.

function fib(n)
     var previousFib := 0, currentFib := 1
     if n = 0
         return 0
     if n = 1
         return 1
     repeat n − 1 times
         var newFib := previousFib + currentFib
         previousFib := currentFib
         currentFib := newFib
     return currentFib

برتری این روش به روش قبلی در این است که در این روش حتی به فضای ذخیره از مرتبه n هم نیازی نیست. فضای ذخیره از مرتبه ۱ کفایت می‌کند. علت این که همیشه از رویکرد پایین به بالا استفاده نمی‌کنیم این است که گاهی از قبل نمی‌دانیم باید کدام زیرمسئله‌ها را حل کنیم تا به مرحله اصلی برسیم، یا این که مجبوریم زیرمسئله‌هایی که استفاده نمی‌شوند را هم حل کنیم.

تفاوت این روش و روش تقسیم و غلبه (تقسیم و حل)

یکی از روش‌های پرکاربرد و مشهور طراحی الگوریتم روش برنامه‌نویسی پویا (یا برنامه‌ریزی پویا - Dynamic Programming) است. این روش همچون روش تقسیم و حل (Divide and Conquer) بر پایه تقسیم مسئله بر زیرمسئله‌ها کار می‌کند. اما تفاوت‌های چشم‌گیری با آن دارد.

زمانی که یک مسئله به دو یا چند زیرمسئله تقسیم می‌شود، دو حالت ممکن است پیش بیاید:

1. داده‌های زیرمسئله‌ها هیچ اشتراکی با هم نداشته و کاملاً مستقل از هم هستند. نمونه چنین مواردی مرتب‌سازی آرایه‌ها با روش ادغام یا روش سریع است که داده‌ها به دو قسمت تقسیم شده و به صورت مجزا مرتب می‌شوند. در این حالت داده‌های یکی از بخش‌ها هیچ ارتباطی با داده‌های بخش دیگر نداشته و در نتیجهٔ حاصل از آن بخش، اثری ندارند. معمولاً روش تقسیم و حل برای چنین مسائلی کارایی خوبی دارد.
2. داده‌های زیرمسئله وابسته به هم بوده یا با هم اشتراک دارند. در این حالت به اصطلاح زیرمسئله‌ها هم‌پوشانی دارند. نمونه بارز چنین مسائلی محاسبه جمله nام دنباله اعداد فیبوناچی است.

روش برنامه‌نویسی پویا غالباً برای الگوریتم‌هایی به کار برده می‌شود که در پی حل مسئله‌ای به صورت بهینه می‌باشند.

در روش تقسیم و غلبه ممکن است برخی از زیرمسائلِ کوچکتر، با هم برابر باشند که در این صورت زیرمسائلِ برابر، به‌طور تکراری چندین مرتبه حل می‌شوند که این یکی از معایب روش تقسیم و غلبه است.

ایده‌ای که در فرایِ روش برنامه‌نویسی پویا نهفته‌است، جلوگیری از انجام این محاسبات تکراری است و روشی که معمولاً برای این عمل به کارگرفته می‌شود استفاده از جدولی برای نگهداری نتایج حاصل از حل زیرمسائل است. در این صورت اگر الگوریتم به زیرمسئله‌ای برخورد کرد که پیش از این حل شده است، به جای حل مجدد آن، نتیجه محاسبه قبلی را از جدول برداشته و کار را با زیرمسئله بعدی دنبال می‌کند.

روش برنامه‌نویسی پویا یک روش پایین به بالا است (البته همان‌طور که گفته شد، اگر از قبل بدانیم باید کدام زیرمسئله‌ها را حل کنیم تا به مرحله اصلی برسیم، یا این که مجبور نباشیم زیرمسئله‌هایی که استفاده نمی‌شوند را هم حل کنیم) به این معنی که از حل مسائل کوچکتر به حل مسائل بزرگتر می‌رسیم. در حالیکه از نظر ساختاری، روش تقسیم و غلبه روشی است از بالا به پایین، یعنی به‌طور منطقی (نه عملی) پردازش از مسئله اولیه آغاز شده و به سمت پایین و حل مسائلِ کوچکتر، به پیش می‌رود.

مجموع زیرمجموعه و کوله پشتی: اضافه کردن یک متغیر

ما بیشتر و بیشتر می‌بینیم که مسائل مربوط به برنامه‌ریزی منبع خیلی خوبی از مسایل الگوریتمی را با انگیزهٔ عملی ارائه می‌دهد. تاکنون مشکلاتی را در نظر گرفتیم که در آن درخواست‌ها با فاصلهٔ زمانی مشخص از یک منبع مشخص‌شده و همچنین مشکلاتی که در آن درخواست‌ها دارای مدت و مهلت هستند، اما فواصل خاصی را که در طی آن باید انجام شود تعیین نشده‌است. در این بخش، ما نسخه‌ای از نوع دوم مشکل را با مدت زمان و مهلت در نظر می‌گیریم، که حل مستقیم با استفاده از تکنیک‌هایی که تاکنون دیده‌ایم، دشوار است.

ما برای حل مسئله از برنامه‌نویسی پویا استفاده خواهیم کرد، اما با یک تغییر: مشخص می‌شود مجموعه زیرمسئله‌ها به اندازه کافی نخواهدبود، و بنابراین ما در نهایت به ایجاد یک مجموعه غنی‌تر از زیرمسئله‌ها می‌پردازیم. همان‌طور که خواهیم‌دید، این کار با اضافه کردن یک متغیر جدید به بازگشت در زیربرنامهٔ پویا انجام می‌شود.

مسئله

در مسئلهٔ برنامه‌ریزی که در اینجا مورد توجه قرار می‌دهیم، ما یک ماشین داریم که می‌تواند دستورها را پردازش کند همچنین یک سری درخواست‌ها ${\displaystyle 1,2,\ldots ,n}$ داریم که می‌توانیم از آن در بازهٔ زمانی ${\displaystyle 0}$ تا ${\displaystyle W}$ استفاده کنیم. هر درخواست مربوط به یک دستور است که برای پردازش آن به ${\displaystyle w_{i}}$ واحد زمانی نیاز داریم. اگر هدف ما این باشد که دستورها را پردازش کنیم به طوری که ماشین را تا زمان ${\displaystyle W}$ مشغول نگه داریم، کدام دستورها را باید انتخاب کنیم؟

به زبان دقیق تر، فرض کنید که ما آیتم‌های ${\displaystyle 1,2,\ldots ,n}$ را داریم، که هر کدام دارای وزن ${\displaystyle w_{i}}$ است. هدف ما انتخاب یک زیرمجموعه از این آیتم‌ها است به طوری که مجموع ${\displaystyle w_{i}}$های آیتم‌های انتخاب شده از ${\displaystyle W}$ کمتر مساوی باشند و با توجه به این محدودیت، مجموع این وزن‌ها بیشترین مقدار ممکن باشد. ما این مسئله را «مسئلهٔ مجموع زیرمجموعه» می‌نامیم.

این مسئله یک حالت خاص رایج از مسئلهٔ کوله پشتی است، که هر درخواست ${\displaystyle i}$ یک ارزش ${\displaystyle v_{i}}$ و یک‌وزن ${\displaystyle w_{i}}$ دارد. هدف در این مسئلهٔ کلی‌تر این است که زیرمجموعه‌ای با بیشترین مجموع ارزش انتخاب کنیم با توجه به اینکه نباید مجموع وزن‌ها از ${\displaystyle W}$ بیشتر باشد. به‌طور معمول مسئلهٔ کوله پشتی یک زیرمسئله از مسائل کلی‌تر است. نام «کوله پشی» اشاره به مسئلهٔ پر کردن یک کوله پشتی با ظرفیت ${\displaystyle W}$ دارد که باید آن را تا جای ممکن با استفاده از مجموعه ای از آیتم‌ها پرکرد. ما از واژهٔ وزن یا زمان برای اشاره به ${\displaystyle W}$، ${\displaystyle w_{i}}$ استفاده خواهیم کرد.

چون این مسئله، مسائل برنامه‌ریزی دیگری که قبلاً دیده‌ایم را شبیه‌سازی می‌کند، طبیعی است که از خود بپرسیم آیا الگوریتم حریصانه‌ای برای راه‌حل بهینه وجود دارد یا خیر. به نظر می‌آید که پاسخ خیر باشد، حداقل تا کنون هیچ روش حریصانهٔ کارایی شناخته نشده‌است که آیتم‌ها را به صورت نزولی مرتب کند؛ یا حداقل این کار را برای آیتم‌های با وزن حداکثر ${\displaystyle W}$ انجام دهد، و سپس ما شروع به انتخاب آیتم‌ها با این ترتیب کنیم تا جایی که مجموع وزن آیتم‌های انتخاب شده کمتر از ${\displaystyle W}$ باشد. اما اگر ${\displaystyle W}$ مضرب دو باشد، و ما سه آیتم با وزن‌های ${\displaystyle \{{\frac {w}{2}},{\frac {w}{2}},{\frac {w}{2}}+1\}}$ داشته‌باشیم، خواهیم دید که الگوریتم حریصانه جواب بهینه را تولید نخواهد کرد. به‌طور جایگزین می‌توانستیم آیتم‌ها را بر اساس وزنشان به صورت صعودی مرتب کنیم و کار مشابه را انجام دهیم، ولی این بار در ورودی‌های ${\displaystyle \{{\frac {w}{2}},{\frac {w}{2}},1\}}$ شکست می‌خورد.

هدف ما این است که نشان دهیم که چگونه با استفاده از برنامه‌نویسی پویا این مسئله را حل کنیم. اصول اولیهٔ برنامه‌نویسی پویا را به یاد بیاورید: ما باید تعداد کمی از زیرمسئله‌ها را داشته باشیم به طوری که هر زیرمسئله را بتوان به راحتی با استفاده از زیرمسئله‌های «کوچکتر» حل کرد و پاسخ به مسئلهٔ اصلی براحتی بدست می‌آید، هنگامی که ما پاسخ همهٔ زیر مسئله‌ها را بدانیم.

طراحی الگوریتم

می‌خواهیم از تعداد زیادی زیرمسئله استفاده کنیم. در واقع برای هر مجموعهٔ اولیه ${\displaystyle \{1,\ldots ,i\}}$ از آیتم‌ها و هر مقدار ممکن w برای بیشینه وزن ممکن، زیرمسئله‌ای در نظر می‌گیریم تا با استفاده از آنها بتوانیم سریعتر مسئله را حل کنیم. فرض کنید که ${\displaystyle W}$ یک عدد صحیح باشد و همهٔ درخواست‌های ${\displaystyle i=1,2,\ldots ,n}$ مقادیر صحیح ${\displaystyle w_{i}}$ هستند. ما یک زیرمسئله به ازای هر ${\displaystyle i=1,2,\ldots ,n}$ و هر ${\displaystyle w\leq W}$ داریم. ما ${\displaystyle opt(i,w)}$ را به عنوان مقدار پاسخ بهینه برای آیتم‌های ${\displaystyle 1,2,\ldots ,i}$ و بیشینه وزن مجاز ${\displaystyle w}$ تعریف می‌کینم که برابر است با:

${\displaystyle opt(i,w)=\max _{s}\Sigma _{s}w_{j}}$

که ${\displaystyle \max }$ روی زیرمجموعهٔ ${\displaystyle s\in \{1,\ldots ,i\}}$ است که ${\displaystyle w_{i}\leq W}$ را ارضا می‌کند. استفاده از این مجموعهٔ جدید از زیرمسئله‌ها، این اجازه را به ما می‌دهد که مقدار ${\displaystyle opt(i,w)}$ به عنوان یک عبارت ساده بر حسب مقادیر بدست آمده از مسائل کوچکتر بیان کرد. علاوه بر این ${\displaystyle opt(i,w)}$ کمیتی است که ما در انتها به دنبال آن هستیم. فرض کنید که o نمایانگر راه‌حل بهینه برای مسئلهٔ اصلی باشد. دو حالت داریم:

۱- اگر ${\displaystyle n\notin o}$ آنگاه ${\displaystyle opt(n,W)=opt(n-1,W)}$ پس به راحتی می‌توانیم عبارت ${\displaystyle n}$ را نادیده بگیریم.

۲- اگر ${\displaystyle n\in o}$ آنگاه ${\displaystyle opt(n,W)=w_{n}+opt(n-1,W-w_{n})}$، از این به بعد ما به دنبال استفاده از ظرفیت باقی‌ماندهٔ ${\displaystyle W-w_{n}}$ هستیم.

هنگامی که آیتم nام بسیار بزرگ است، ${\displaystyle w_{n}>W}$ ما باید داشته باشیم ${\displaystyle opt(n,W)=opt(n-1,W)}$. در غیر این صورت، ما راه‌حل بهینه را از این طریق با توجه به اینکه برای هر n درخواست کدام یک از گزینه‌های بالا بهتر است بدست می‌آوریم. با استفاده از استدلال مشابه برای زیرمسئلهٔ آیتم‌های ${\displaystyle \{1,\ldots ,i\}}$ و بیشینه وزن ${\displaystyle w}$، رابطهٔ بازگشتی روبرو را می‌دهد:

(*)

اگر ${\displaystyle w_{i}>W}$ آنگاه${\displaystyle opt(i,W)=opt(i-1,W)}$. در غیر اینصورت:${\displaystyle opt(i,w)=\max\{opt(i-1,w),w_{i}+opt(i-1,w-w_{i})\}}$

مانند قبل، ما می‌خواهیم الگوریتمی طراحی کنیم که جدولی از همهٔ مقادیر ممکن ${\displaystyle opt(i,w)}$ داشته باشیم درحالی که هر کدام از آنها را حداکثر یکبار محاسبه کرده باشیم.

با استفاده از لم (*) می‌توان فوراً ثابت کرد که مقدار برگشتی ${\displaystyle M[n,W]}$ برای در خواست‌های ${\displaystyle 1,2,\ldots ,n}$ و وزن در دسترس ${\displaystyle W}$، پاسخ بهینه‌ای است .(${\displaystyle M}$ یک آرایهٔ دو بعدی است که مقادیر ${\displaystyle opt(i,w)}$ را در خود ذخیره کرده‌است)

آنالیز آلگوریتم

برای الگوریتمی که در این شرایط طراحی کرده‌ایم، اما به یک جدول دو بعدی نیاز داریم، که بازتاب دو بعدی جدول زیرسوالات است که در حال ساخته شدن هستند. به عنوان یک مثال از اجرای این الگوریتم، به یک نمونه با وزن ${\displaystyle W=6}$ و ${\displaystyle n=3}$ و آیتم‌هایی با اندازه ${\displaystyle w_{1}=w_{2}=2}$ و ${\displaystyle w_{3}=3}$ توجه کنید. ما در خواهیم یافت که مقدار بهینه ${\displaystyle opt(3,6)=6}$ خواهدبود (که با استفاده از سومین آیتم و یکی از دو آیتم اول آن را بدست آورده‌ایم).

قبل از آن، در مورد برنامه‌ریزی فواصل زمانی موزون، جدول راه حل‌های ${\displaystyle M}$ را ساخته‌ایم، و مقادیر ${\displaystyle M[i,W]}$ را با استفاده از مقادیر قبلی در زمان اجرای ${\displaystyle {\mathcal {O}}(1)}$محاسبه می‌کنیم؛ بنابراین مدت زمان اجرا متناسب با تعداد ورودی‌ها به جدول می‌باشد.

(**)

الگوریتم مجموع زیرمجموعه ${\displaystyle (n,w)}$ بهینه جواب مسئله را محاسبه می‌کند و زمان اجرای آن ${\displaystyle {\mathcal {O}}(nw)}$ است.

توجه کنید که زمان اجرای برنامه تابعی از چندجمله‌ای بر حسب n نیست، در واقع یک تابع چندجمله ای از ${\displaystyle n}$ و ${\displaystyle w}$ است. ما چنین الگوریتم‌هایی را «شبه چندجمله‌ای» می‌نامیم. الگوریتم‌های شبه‌چندجمله‌ای می‌توانند به‌طور قابل توجهی کارا باشند هنگامی که اعداد ${\displaystyle \{w_{i}\}}$ی که به عنوان ورودی دریافت می‌کنیم به‌طور قابل توجهی کوچک باشند. هرچند هنگامی که ${\displaystyle {w_{i}}}$ها بزرگ می‌شوند عملکرد این الگوریتم‌ها کاهش می‌یابد.

برای بدست آوردن یک مجموعه بهینه ${\displaystyle s}$ از آیتم‌ها، می‌توانیم آرایهٔ ${\displaystyle M}$ را با استفاده از روشی که در قبل گفته شد ردیابی کنیم.

(***)

یک جدول ${\displaystyle M}$ از بهینه مقدارهای زیرمسئله‌ها داده شده‌است. بهترین مجموعه ${\displaystyle s}$ را می‌توان در زمان ${\displaystyle {\mathcal {O}}(n)}$ پیدا کرد.

مسئلهٔ کوله پشتی

مسئلهٔ کوله پشتی کمی از مسئلهٔ برنامه‌ریزی که در قبل بحث کردیم سخت‌تر است. شرایطی را در نظر بگیرید که مانند قبل آیتم ${\displaystyle i}$ یک‌وزن نامنفی ${\displaystyle {w_{i}}}$ دارد و همچنین یک ارزش جداگانه ${\displaystyle {v_{i}}}$ نیز دارد. هدف ما پیدا کردن مجموعه ${\displaystyle s}$ با بیشینه ارزش ${\displaystyle \Sigma v_{i}}$ با محدودیت مجموع وزن این آیتم‌ها نباید از ${\displaystyle W}$ بیشتر شود.

سخت نیست که الگوریتم پویای خود را برای این مسئله کلی تر گسترش دهیم. ما از مجموعه زیرمسئله‌های مشابه استفاده می‌کنیم، ${\displaystyle opt(i,w)}$ تا مقدار راه‌حل بهینه را مشخص کنیم با استفاده از زیرمجموعه از آیتم‌های ${\displaystyle \{1,\ldots ,i\}}$ و بیشینه وزن دردسترس ${\displaystyle w}$. ما یک راه‌حل بهینه ${\displaystyle o}$ در نظرمی‌گیریم و دوحالت را با توجه به اینکه ${\displaystyle n\in o}$ هست یا خیر، مشخص می‌کنیم:

۱- اگر ${\displaystyle n\notin o}$ آنگاه ${\displaystyle opt(n,w)=opt(n-1,w)}$

۲- اگر ${\displaystyle n\in o}$ آنگاه ${\displaystyle opt(n,w)=v_{n}+opt(n-1,w-w_{n})}$

استفاده از این خط از استدلال برای زیرمسئله‌ها نتیجهٔ مشابه (*) را می‌دهد.

(****)

اگر ${\displaystyle w<w_{i}}$ آنگاه ${\displaystyle opt(i,w)=opt(i-1,w)}$. در غیر این صورت: ${\displaystyle opt(i,w)=\max\{opt(i-1,w),v_{i}+opt(i-1,w-w_{i})\}}$

با استفاده از این روش بازگشت، می‌توانیم یه الگوریتم پویای کاملاً مشابه پیاده‌سازی کنیم، که نتیجهٔ روبرو را می‌دهد:

مسئلهٔ کوله پشتی در زمان اجرای ${\displaystyle {\mathcal {O}}(nW)}$ قابل حل است.[9]

الگوریتم ضریب دو جمله‌ای با استفاده از برنامه‌ریزی پویا

ورودی‌ها : اعداد صحیح و مثبت ${\displaystyle n}$ و ${\displaystyle k}$ که در آن ${\displaystyle k\leq n}$ است.

خروجی‌ها : bin2 ضریب دو جمله‌ای ${\displaystyle {\binom {n}{k}}}$

int bin2(int n, int k) 
{ 
    int B[n + 1][k + 1]; 
    for(int i = 0;i <= n;i++) 
        for(int j = 0;j <= min(k, i);j++) 
            if(j == 0 || j == i) 
                B[i][j] = 1; 
            else 
                B[i][j] = B[i - 1][j - 1] + B[i - 1][j]; 
    return B[n][k];
}

محدودیت‌های برنامه‌نویسی پویا: مسئلهٔ فروشندهٔ دوره‌گرد

برنامه‌نویسی پویا همیشه جواب نمی‌دهد. خوب است که علت این موضوع را بدانیم تا از اینکه در دام الگوریتم‌های نادرست و نابهینه بیفتیم، خودداری کنیم. ابتدا به بررسی مسئلهٔ زیر می‌پردازیم:

مسئله: بلندترین مسیر ساده

ورودی: یک گراف وزن دار ${\displaystyle G}$ با راس‌های شروع و پایان ${\displaystyle s,t}$ داریم .

خروجی: مسیری از ${\displaystyle s}$ به ${\displaystyle t}$ بیابید که بیشترین وزن را داشته باشد و در آن هیچ رأسی را بیش از یک بار نبینیم.

این مسئله از دو جهت با مسالهٔ فروشندهٔ دوره‌گرد(TSP) متفاوت است. اولاً، این مسئله به دنبال یک مسیر است نه یک تور بسته. این تفاوت قابل توجه نیست: به راحتی با اضافه کردن یال ${\displaystyle (t,s)}$ یک تور بسته به دست می‌آوریم. ثانیاً این مسئله به دنبال مسیر با بیشترین وزن است به جای مسیر با کمترین وزن. باز هم این تفاوت خیلی مهم نیست: این مسئله ما را تشویق می‌کند تا جایی که می‌توان راس‌ها را بازدید کرد (در حالت ایدئال تمام رئوس) دقیقاً مانند TSP. نکتهٔ مهم در این مسئله این است که ما نیابد از هیچ رأسی بیش از یک بار عبور کنیم.

برای گراف‌های غیر وزندار، بزرگترین مسیر از ${\displaystyle s}$ به ${\displaystyle t}$ حداکثر ${\displaystyle n-1}$ یال دارد. پیدا کردن چنین «مسیرهای همیلتونی» یک مسئلهٔ مهم در نظریه گراف است.

چه زمان‌هایی الگوریتم‌های برنامه‌نویسی پویا درست هستند؟

درستی الگوریتم‌های برنامه‌نویسی پویا وابسته به روابط بازگشتی‌ای است که بر پایه آن بنا شده‌اند. فرض کنید ما تابع ${\displaystyle LP[i,j]}$ را به عنوان تابعی که نمایانگر طول بلندترین مسیر ساده از ${\displaystyle i}$ به ${\displaystyle j}$ است تعریف کنیم. توجه کنید که بلندترین مسیر ساده از ${\displaystyle i}$ به ${\displaystyle j}$ باید قبل از رسیدن به ${\displaystyle j}$، تعدادی رئوس ${\displaystyle x}$ را بازید کند؛ بنابراین، آخرین یال بازدید شده باید به صورت ${\displaystyle (x,j)}$ باشد. این موضوع رابطهٔ بازگشتی روبرو را برای محاسبهٔ طول بلندترین مسیر ساده پیشنهاد می‌کند:

${\displaystyle LP[i,j]=\max _{(x,j)\in E}LP[i,x]+c(x,j)}$

که در آن ${\displaystyle c(x,j)}$ وزن یال ${\displaystyle (x,j)}$ است.

ایده به نظر معقول می‌رسد، اما شما می‌توانید مشکلات را ببینید؟ به دو مورد زیر توجه کنید:

اولاً، این رابطهٔ بازگشتی منجر به هیچگونه سادگی نمی‌شود. ما از کجا می‌دانیم که راس ${\displaystyle j}$ قبلاً در بلندترین مسیر ساده از ${\displaystyle i}$ به ${\displaystyle x}$ ظاهر نشده‌است؟ اگر ظاهر شده باشد، آنگاه اضافه کردن یال ${\displaystyle (x,j)}$ منجر به ایجاد دور در گراف می‌شود. برای جلوگیری از چنین چیزی، ما باید یک تابع بازگشتی متفاوت تعریف کنیم که صراحتاً ذخیره کند که ما در چه مکان‌هایی حضور داشتیم. شاید بتوانیم ${\displaystyle LP'[i,j,k]}$ را تعریف کنیم به عنوان تابعی که نمایانگر بلندترین مسیر ساده از ${\displaystyle i}$ به ${\displaystyle j}$ است و از راس ${\displaystyle k}$ عبور نمی‌کند؟ شاید این یک قدم در جهت درست باشد ولی هنوز ما را به یک تابع بازگشتی قابل اطمینان نمی‌رساند.

مشکل دوم مربوط به دستورالعمل ارزیابی است. ابتدا چه چیزی را ارزیابی می‌کنید؟ چون هیچ ترتیب چپ به راست یا بزرگ به کوچکی از رئوس وجود ندارد، واضح نیست که زیرمسئله‌های کوچکتر چه هستند. بدون داشتن چنین ترتیبی، ما در یک دور بینهایت می‌افتیم تا زمانی که بخواهیم کاری انجام دهیم.

برنامه‌نویسی پویا را می‌توان در هر مسئله‌ای که اصل بهینه بودن را رعایت می‌کند بکار برد. برای مثال، در تصمیم‌گیری اینکه یک تطابق رشته‌ای را بوسیله جابه‌جایی، اضافه کردن یا حذف کردن گسترش دهیم، ما نیازی نداریم که بدانیم کدام دنباله از عملگرها تا آن زمان انجام شده‌است. در واقع، ممکن است دنباله‌های متفاوت ویرایش وجود داشته باشد که هزینهٔ ${\displaystyle C}$ را بر روی ${\displaystyle p}$ حرف از الگوی ${\displaystyle P}$ و ${\displaystyle t}$ حرف از الگوی ${\displaystyle T}$ اعمال می‌کند.

مسئله‌ها هنگامی از اصل بهینگی پیروی نمی‌کنند که به جای هزینهٔ عملیات، مشخصهٔ عملیات مهم می‌شود. چنین چیزی می‌تواند شکلی از مسئلهٔ فاصلهٔ ویرایش که در آن مجاز به استفاده از عملگرها با یک ترتیب خاص نیستیم، باشد. هر چند بسیاری از مسائل ترکیبیات از اصل بهینگی پیروی می‌کنند.

چه زمانی الگوریتم‌های برنامه‌نویسی پویا کارا هستند؟

زمان اجرای الگوریتم‌های برنامه‌نویسی پویا تابع دو چیز است :۱) تعداد زیر مسئله‌هایی که ما باید آنها را بررسی کنیم ۲) چه قدر طول می‌کشد تا هر زیرمسئله را بررسی کنیم. مورد اول – که معمولاً فضای حالات نامیده‌می‌شود – مشکل جدی‌تری است. تاکنون در مسئله‌هایی که بررسی کردیم، زیر مسئله‌ها بوسیلهٔ مکان‌های توقف در ورودی مشخص می‌شدند. این به این خاطر است که موضوعات ترکیبیاتی که روی آنها کار می‌شده مانند رشته‌ها، دنباله‌های عددی، چندضلعی‌ها و … به صورت ضمنی در عناصر خود دارای یک ترتیب هستند. این ترتیب را نمی‌توان به هم زد مگر با عوض کردن صورت مسئله. هنگامی که ترتیب مشخص شد، مکان‌های توقف یا حالات نسبتاً کمی وجود خواهد داشت، به طوری که ما می‌توانیم الگوریتم‌های بهینه را بدست بیاوریم.

هنگامی که اشیا به صورت مشخص دارای یک ترتیب نیستند، ما تعداد نمایی از زیر مسئله‌ها را بدست می‌آوریم (برخلاف بالا). فرض کنید حالات زیرمسئله ما شامل کل مسیرها از راس شروع تا مقصد است. پس ${\displaystyle LP[i,j,P]}$ مشخص کنندهٔ بلندترین مسیر ساده از ${\displaystyle i}$ تا ${\displaystyle j}$ است که ${\displaystyle P}$ دنبالهٔ دقیق رئوس میانی بین ${\displaystyle i}$ و ${\displaystyle j}$ است که در مسیر آمده‌است. رابطهٔ بازگشتی روبرو برای محاسبهٔ مقدار بالا است که در آن ${\displaystyle P+x}$ به معنی اضافه کردن ${\displaystyle x}$ به انتهای ${\displaystyle P}$ است:

${\displaystyle LP[i,j,P+x]=\max _{(x,j)\in E,x,j\notin P}LP[i,x,P]+c(x,j)}$

این رابطه درست است اما چه قدر بهینه است؟ مسیر ${\displaystyle P}$ شامل حداکثر ${\displaystyle n-3}$ راس با یک ترتیب مشخص است. پس ما ${\displaystyle (n-3)!}$ از چنین مسیرهایی داریم، در واقع، این الگوریتم واقعاً از جستجوی ترکیبیاتی استفاده می‌کند تا تمامی مسیرهای بین را بسازد.

ما با این ایده می‌توانیم یک کار بهتر انجام دهیم. فرض کنید که ${\displaystyle LP'[i,j,S]}$ مشخص‌کنندهٔ بلندترین مسیر از ${\displaystyle i}$ به ${\displaystyle j}$ است که رأس‌های میانی روی مسیر دقیقاً در مجموعه ${\displaystyle S}$ قرار دارد. بنابر این اگر ${\displaystyle S=\{a,b,c\}}$، دقیقاً ۶ مسیر وجود دارد:

${\displaystyle S:iabcj,iacbj,ibacj,ibcaj,icabj,icbaj}$

این فضای حالت حداکثر ${\displaystyle 2^{n}}$ حالت دارد، بنابراین کوچکتر از مسیرهای محاسبه شده در قسمت قبل است. علاوه بر این، تابع را می‌توان با رابطه بازگشتی روبرو محاسبه کرد:

${\displaystyle LP'[i,j,S\cup \{x\}]=\max _{(x,j)\in E,x,j\notin S}LP[i,x,S]+c(x,j)}$

پس می‌توان بلندترین مسیر ساده از ${\displaystyle i}$ به ${\displaystyle j}$ را با بیشینه کردن روی مجموعهٔ تمام رئوس بین این دو رأس به دست آورد.

${\displaystyle LP[i,j]=\max _{S}LP'[i,j,S]}$

تنها ${\displaystyle 2^{n}}$ زیر مجموعه از ${\displaystyle n}$ راس وجود دارد، پس این یک بهبود چشمگیر روی شمردن تمام ${\displaystyle n!}$ تور ممکن است. در واقع این روش می‌تواند برای حل TSP هنگامی که بیش از ۳۰ رأس داریم استفاده شود. همچنان برنامه‌نویسی پویا بیشترین تأثیر را بر اشیایی که به صورت مناسب مرتب شده‌اند دارد.[10]

الگوریتم‌هایی که از برنامه‌نویسی پویا استفاده می‌کنند

• جواب‌های بازگشت‌کننده به مدل‌های مشبک برای به هم پیوستن پروتئین و دی‌ان‌ای
• استنتاج معکوس به عنوان راه حلی برای مسائل بهینه‌سازی پویای زمان‌گسسته با افق متناهی
• روش ضرایب نامعین را می‌توان برای حل معادلهٔ بلمن در مسائل بهینه‌سازی پویای زمان‌تغییرناپذیر تنزیلیافتهٔ زمان‌گسسته با افق نامتناهی به کار برد.
• بسیاری از الگوریتم‌های رشته از جمله بلندترین زیردنبالهٔ مشترک،[11] بلندترین زیردنبالهٔ صعودی، بلندترین زیررشتهٔ مشترک، فاصلهٔ لونشتاین[12]
• بسیاری از مسائل الگوریتمی گرافها را می‌توان به صورت بهینه برای گراف‌هایی با عرض درخت یا خوشهٔ کران‌دار توسط برنامه‌نویسی پویا روی تجزیهٔ درختی گراف حل کرد.
• الگوریتم کاک-یانگر-کاسامی(CYK) که امکان و چگونگی ساخت یک رشته توسط یک گرامر مستقل از متن را تعیین می‌کند
• الگوریتم کنوث برای شکستن خط که ناهمواری را کمینه می‌کند
• کاربرد جدول جابجایی و تکذیب در شطرنج کامپیوتری
• الگوریتم ویتربی[13] (استفاده‌شده برای مدل‌های نهان مارکوف و به‌طور خاص برچسب‌زنی اجزای کلام)

پانویس

1. هیلیر، ج 2، ص 65
2. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. p. 378.
3. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. pp. 379-383.
4. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. pp. 384-386.
5. «Introduction to Dynamic Programming | 20bits». بایگانی‌شده از اصلی در ۳ نوامبر ۲۰۰۸. دریافت‌شده در ۲۵ ژوئیه ۲۰۱۱.
6. «Memoize - perldoc.perl.org». perldoc.perl.org. دریافت‌شده در ۲۰۱۹-۱۲-۰۵.
7. «Memoization». www.metalevel.at. دریافت‌شده در ۲۰۱۹-۱۲-۰۵.
8. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. pp. 367-368.
9. Kleinberg, Jon; Tardos, Éva (2005). Algorithm Design. Pearson. ISBN 978-0-321-29535-4. pp. 266-272.
10. Skiena, Steven S. (2008). The Algorithm Design Manual. Springer. ISBN 978-1849967204. pp. 301-304.
11. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. pp. 390-396.
12. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. pp. 306-408.
13. Cormen, Thomas H. ; Leiserson, Charles E. ; Rivest, Ronald L. ; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4. pp. 408-409.

منابع

• هیلیر، فردریک؛ لیبرمن، جرالد. ج (۱۳۸۲). تحقیق در عملیات، ترجمه محمد مدرس و اردوان آصف‌وزیری، تهران: نشر جوان، چاپ دهم.
• نیپولیتان، ریچارد؛ نعیمی‌پور، کیومرث (۱۳۹۰). طراحی الگوریتم‌ها، ترجمه عین‌الله جعفرنژاد قمی، بابل: انتشارات علوم رایانه.

پیوند به بیرون

• An Introduction to Dynamic Programming
• Dyna, a declarative programming language for dynamic programming algorithms
• Wagner, David B. , 1995, "Dynamic Programming." An introductory article on dynamic programming in متمتیکا.
• Ohio State University: CIS 680: class notes on dynamic programming, by Eitan M. Gurari
• A Tutorial on Dynamic programming
• MIT course on algorithms - Includes a video lecture on DP along with lecture notes—See lecture 15.
• More DP Notes
• King, Ian, 2002 (1987), "A Simple Introduction to Dynamic Programming in Macroeconomic Models." An introduction to dynamic programming as an important tool in economic theory.
• Dynamic Programming: from novice to advanced A TopCoder.com article by Dumitru on Dynamic Programming
• Algebraic Dynamic Programming - a formalized framework for dynamic programming, including an entry-level course to DP, University of Bielefeld
• Dreyfus, Stuart, "Richard Bellman on the birth of Dynamic Programming."
• Dynamic programming tutorial

• الگوریتمستان، روش برنامه‌نویسی پویا

جستارهای وابسته

• معادلات بلمن
• برنامه‌ریزی خطی
• فرایند مارکف
• ضرب زنجیره‌ای ماتریس
• مسئله یافتن کوتاهترین مسیر