بهینه‌سازی خطی عدد صحیح

بهینه‌سازی خطی عدد صحیح (به انگلیسی: Integer Linear Optimization) زیر شاخه‌ای از بهینه‌سازی ریاضی است که مسایل آن مشابه مسایل بهینه‌سازی خطی است، با این تفاوت که همه یا برخی از متغیر (مجهول)های مسئله عدد صحیح هستند. همانند بهینه‌سازی خطی، هدف برنامه‌ریزی عدد صحیح پیدا کردن مقدار کمینه یا بیشینه از یک تابع خطی بر روی فضایی با محدودیت‌هایی خطی است، اما به دلیل وجود متغیرهای گسسته این فضا پیوسته و محدب نیست بلکه فضایی گسسته (در نتیجه نامحدب) است. چنانچه تعدادی از متغیرها به صورت اعداد صحیح و بقیه متغیرها به صورت اعداد غیر صحیح بیان شوند، مسئله از نوع بهینه‌سازی خطی ترکیبی (به انگلیسی: mixed-integer linear programming)، که به اختصار MILP هم گفته می‌شود، خواهد بود.

فرم متعارف

فرم متعارف مسئلهٔ بهینه‌سازی عدد صحیح به این صورت بیان می‌شود:

${\displaystyle {\begin{aligned}&{\text{maximize}}&&\mathbf {c} ^{\mathrm {T} }\mathbf {x} \\&{\text{subject to}}&&A\mathbf {x} \leq \mathbf {b} ,\\&&&\mathbf {x} \geq \mathbf {0} ,\\&{\text{and}}&&\mathbf {x} \in \mathbb {Z} ^{n},\end{aligned}}}$

با بکار بردن متغیرهای کمکی می‌توان فرم متعارف را به به فرم استاندارد تبدیل کرد:

${\displaystyle {\begin{aligned}&{\text{maximize}}&&\mathbf {c} ^{\mathrm {T} }\mathbf {x} \\&{\text{subject to}}&&A\mathbf {x} +\mathbf {s} =\mathbf {b} ,\\&&&\mathbf {s} \geq \mathbf {0} ,\\&&&\mathbf {x} \geq \mathbf {0} ,\\&{\text{and}}&&\mathbf {x} \in \mathbb {Z} ^{n},\end{aligned}}}$

با این کار نامساوی‌ها به تساوی تبدیل می‌شوند. در این مدل b بردار منابع، c بردار هزینه و A ماتریس ضرایب می‌باشد.

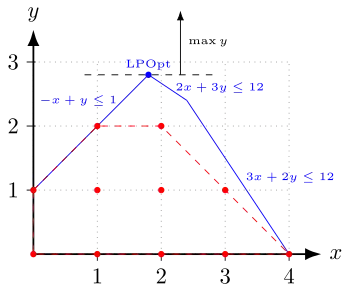
مثال زیر را در نظر بگیرید:

${\displaystyle {\begin{aligned}\max &{\text{ }}y\\-x+y&\leq 1\\3x+2y&\leq 12\\2x+3y&\leq 12\\x,y&\geq 0\\x,y&\in \mathbb {Z} \end{aligned}}}$

نقاط صحیحی که می‌توانند جواب مسئله باشند در شکل با رنگ قرمز نشان داده شده‌اند و خطوط بریده بریده قرمز نشانگر ناحیه امکان‌پذیر برای جواب مسئله است. خطوط آبی، ناحیه ای را نشان می‌دهد که پاسخ مسئله بدون در نظر گرفتن شرط صحیح بودن در آن قرار می‌گیرد.

روش شاخه و کران برای حل مسائل برنامه‌ریزی خطی عدد صحیح

ایده اصلی در این روش تقسیم ناحیه امکان‌پذیر به چند زیر منطقه و بررسی امکان وجود جواب‌های صحیح در این نواحی است. بدین منظور گام‌های زیر پیموده می‌شوند:

1. مسئله خطی اصلی را بدون در نظر گرفتن شرط صحیح بودن متغیرها حل کنید (الف). اگر همه متغیرها مقدار صحیح گرفتند، جواب مسئله بدست آمده‌است. در غیر اینصورت به گام دوم بروید.
2. اگر تابع هدف از نوع Max بود قرار دهید ∞-=ZL در غیر اینصورت قرار دهید ∞+=ZL.
3. شاخه بندی:

یکی از متغیرهای تصمیم‌گیری که عدد صحیح نیست را انتخاب کنید(XJ=X*J) و دو مسئله فرعی P1 و P2 را به صورت زیر ایجاد کنید:

مسئله P1 همان مسئله (الف) می‌باشد با این تفاوت که قید [XJ ≤ [X*j به آن اضافه شده‌است.

مسئله P2 همان مسئله (الف) می‌باشد با این تفاوت که قید [1 +XJ ≤ [X*j به آن اضافه شده‌است.

۴.کران :

مسئله بدست آمده P1 P2 را حل کرده و بهترین مقداری که برای تابع هدف به ازای یک جواب موجه عدد صحیح برای ۲ مسئله مذکور بدست آمده را جایگزین ZL کنید.

۵.شاخه‌های فرعی در یکی از سه وضعیت زیر متوقف می‌شوند :

• تمام متغیرهای تصمیم‌گیری مقداری صحیح باشند
• مسئله فرعی ناشی از انشعاب مسئله اصلی فاقد جواب ناحیه امکان‌پذیر باشد.
• مقدار تابع هدف از مقدار ZL بدتر باشد.

۶.اگر تمامی انشعاب‌ها به انتها رسیدند توقف کنید و مسئله ای که تابع هدف آن مساوی ZL است را انتخاب کنید .جواب این مسئله همان جواب بهینه مسئله ی اصلی است.در غیر اینصورت به گام ۳ بروید.

مثال:

مسئله زیر را در نظر بگیرید ، می‌خواهیم گام‌های ذکر شده را یک به یک طی کنیم تا به جواب بهینه برسیم.

${\displaystyle {\begin{aligned}&Max&&Z=-x_{1}+4x_{2},\\&s.t.&&-10x_{1}+20x_{2}\leq 22\\&&&5x_{1}+10x_{2}\leq 49\\&&&x_{1}\leq 5,\ x_{i}\geq 0,\ {\text{integer's}},\ i=1,\ 2\end{aligned}}}$

پاسخ مسئله بدون در نظر گرفتن شرط صحیح بودن برابر است با (۳٫۸ , ۳) با Z = ۸٫۲

با شاخه بندی بر روی متغیر غیر صحیح X1 و ساخت دو مسئله P1 و P2 داریم:

${\displaystyle {\begin{aligned}&{P_{1}}{:}\ Max&&Z=-x_{1}+4x_{2},\\&s.t.&&-10x_{1}+20x_{2}\leq 22\\&&&5x_{1}+10x_{2}\leq 49\\&&&x_{1}\leq 5,\ x_{1}\geq 4,\ x_{2}\geq 0\end{aligned}}}$

که جواب بهینه برای P1 بدست می‌آید (۴ , ۲٫۹) با Z = ۷٫۶

به همین ترتیب و با ساختن زیر شاخه و حل آنها، جواب بهینه به صورت (۲, ۲) با Z = ۶ خواهد بود.

برنامه‌ریزی خطی ترکیبی یا مختلط

بسیاری از مسائل بهینه‌سازی دارای متغیرهای پیوسته و گسسته (اعداد صحیح) که به صورت خطی و تفکیک‌پذیر در قیدهای محدود کننده و تابع هدف ظاهر می‌شوند. در بسیاری از این نوع مسائل، متغیرهای عدد صحیح از نوع متغیرهای صفر و یک (دو دویی) هستند که تمرکز ما بر آنهاست.

بیشترین کاربرد این گونه مسائل در زمینه تحقیق در عملیات در مسائل تخصیص، زمان‌بندی و هزینه ثابت شبکه ای مطرح می‌شود. همچنین در زمینه مهندسی شیمی (فرآیندهای اختلاط، طراحی شبکه‌های انتقال و کنترل) کاربرد این مدل‌سازی بیشتر است. این کاربردها شامل کمترین تعداد جفت در ترکیبات انتقال گرما، بهینه‌سازی مصرف انرژی در برج‌های تقطیر، ترکیبات محصولات ستون تقطیر چند منظورهٔ چند مولفه ای، آنالیز انعطاف‌پذیری فرایندهای شیمی، زمان‌بندی دسته‌های ترکیبی و زمینه‌های دیگر می‌باشد.

فرمول بندی

فرمول بندی مسائل بهینه‌سازی خطی ترکیبی معمولاً به صورت زیر انجام می‌شود:

${\displaystyle {\begin{aligned}&Min&&Z=c^{t}x+d^{t}y,\\&s.t.&&Ax+By\leq b\\&&&x\geq 0,\ x\in X\subset \mathbb {R} ^{n},\ y\in \{0,\ 1\}^{q}\end{aligned}}}$

در اینجا x یک بردار n تایی از متغیرهای پیوسته، y یک بردار q تایی از متغیرهای صفر و یک، cو d بردارهای پارامتر، A و B ماتریس‌های ضرایب با ابعاد متناسب و b بردار منابع هستند.

مهم‌ترین چالشی که در حل این گونه مسائل با آن روبرو هستیم که خود ناشی از ماهیت ترکیبی نواحی متغیرهای y می‌باشد، این است که هر انتخابی از صفر و یک برای مولفه‌های بردار y یک مسئله برنامه‌ریزی حطی نسبت به متغیر x پدیدمی‌آورد که باید برای حاصل شدن جواب بهینه برای آن حل شود. برای درک بهتر مسئله ای را در نظر بگیرید که ۱۰۰ متغیر صفر و یک در آن وجود داشته باشد. دو به توان صد ترکیب ممکن وجود خواهد داشت که باید حل شوند و این هزینه محاسباتی زیادی در برخواهد داشت.

الگوریتم‌های مطرح شده برای حل مسائل بهینه‌سازی خطی ترکیبی رامی توان به صورت زیر دسته‌بندی کرد:

• روش‌های شاخه و کران
• روش‌های صفحات برشی
• روش‌های تجزیه
• روش‌های منطق پایه

یک مثال عددی:

روند حل به روش شاخه و کران را می‌توان در شبکه روبرو مشاهده کرد:

جواب بدست آمده عبارت است از: Z = ۶، X1 = ۰، (Y1 ,Y2,Y3) = (۱٬۰,۱)

برنامه‌ریزی غیر خطی اعداد صحیح مختلط (ترکیبی)

استفاده از مسائل با متغیرهای پیوسته و اعداد صحیح به همراه روابط غیرخطی بین متغیرهای تصمیم‌گیری در ادبیات تحقیق در عملیات با عنوان برنامه‌ریزی غیرخطی با متغیرهای پیوسته و عدد صحیح شناخته می‌شود. از جمله علومی که با این نوع برنامه‌ریزی سروکار دارد می‌توان مهندسی شیمی، تحقیق در عملیات، مهندسی صنایع، مهندسی مکانیک، اقتصاد، امار، کامپیوتر، مدیریت پروژه و برنامه ریزان پروژه اشاره کرد.

جستارهای وابسته

• برنامه‌ریزی غیرخطی

منابع