الگوریتم فورد–فالکرسون

الگوریتم فورد-فالکرسون، مسئله بیشینه جریان را در شبکه‌های جریان حل می‌کند. این الگوریتم در سال ۱۹۵۶ منتشر شد. نام این الگوریتم به جای الگوریتم ادموندز کارپ هم به کار می‌رود. ایده اصلی این الگوریتم بسیار ساده‌است: تا جایی که راهی از منبع (گره شروع) به چاهک (گره پایانی)، با یال وزن دار وجود دارد، می‌توان جریان را از یکی از این مسیرها عبور داد. سپس مسیر دیگری پیدا می‌شود و همین طور الگوریتم ادامه پیدا می‌کند.

الگوریتم

در گراف داده شده G با ظرفیت c و جریان f(u،v)=۰ برای یالی از ${\displaystyle u}$ به ${\displaystyle v}$ می‌خواهیم بیشترین جریان از منبع s به چاهک t را پیدا کنیم. بعد از هر مرحله در الگوریتم موارد زیر پیش می‌آید:

• ${\displaystyle f(u,v)\leq c(u,v)}$: جریانی از ${\displaystyle u}$ به ${\displaystyle v}$ از ظرفیت بیشتر نمی‌شود.
• ${\displaystyle \ f(u,v)=-f(v,u)}$: شبکه جریان بین ${\displaystyle u}$ و ${\displaystyle v}$ را نگهداری می‌کند.
• ${\displaystyle \sum f(u,v)=0\iff f_{in}(u)=f_{out}}$: به ازای هر گره ${\displaystyle u}$ به جز چاهک و منبع. مقدار جریان ورودی گره برابر جریان خروجی گره‌است.

در صورت برقراری این سه شرط، شبکه یک جریان قانونی بعد از هر مرحله خواهد داشت. ما شبکه پسماند را اینگونه تعریف می‌کنیم، شبکه پسماند ${\displaystyle G_{f}(V,E_{f})}$ شبکه ایست که ظرفیتش اینگونه بدست می‌آید: ${\displaystyle C_{f}(u,v)=c(u,v)-f(u,v)}$

توجه کنید که ممکن است جریانی از ${\displaystyle v}$ به ${\displaystyle u}$ وجود داشته باشد، که در شبکه‌های پسماند قانونی است ولی در شبکه اصلی غیر مجاز است: اگر f(u،v)>۰ و c(v،u)=۰ آنگاه cf(v،u)>۰.

الگوریتم

• ورودی: گراف G با ظرفیت c، یک منبع s و یک چاه t.
• خروجی: بیشترین جریان f از s به t.
• ۱»برای تمام یال‌هاf(u،v)→۰
• ۲»تا زمانی که مسیر P از s به t در G وجود دارد،

{Cfp=min {cf(u،v)|(u.v) ϵP را پیدا کن. برای هر یال عضو p داریم f(u،v)⟵ f(u,v) + Cfp , f(v،u)⟵ f(v,u) - Cfp برای پیدا کردن مسیر در مرحله ۲ می‌توان از الگوریتم‌های بی اف اس یا DFS استفاده کرد. وقتی که مسیر دیگری در مرحله ۲ پیدا نشود، s به t در شبکه پشماند نمی‌رسد. اگر S مجموعه‌ای از گره‌های قابل دست رسی برای s در شبکهٔ پشماند باشد، آنگاه مجموع ظرفیت در شبکه اصلی یال‌ها از S به V در یک طرف برابر است با مجوع جریان‌هایی از s به t پیدا کرده‌ایم. این نشان می‌دهد که بیشترین جریان پیدا شده‌است.

تحلیل الگوریتم

زمان اجرای این الگوریتم به این بستگی دارد که مسیر P چگونه انتخاب شود. اگر بد انتخاب شده باشد ممکن است الگوریتم خانمه نیابد: مقدار جریان با تکمبل کردن‌های پیاپی افزایش خواهد یافت، لزوماً به مقدار ماکزیمم جریان همگرایی پیدا نمی‌کند. هر چند اگر مسیر تکمیلی با استفاده از الگوریتم جستجوی اول سطح انتخاب شود الگوریتم با مرتبه زمانی چند جمله‌ای اجرا می‌گردد. در حالت کلی زمان اجرا از (O(E*f است، که E یال‌های گراف و f بیشترین جریان است. چون پیدا کردن هر مسیر از (O(E طول می‌کشد، همچنین از (O(۱طول می‌کشد تا جریانی اضافه شود.

پیاده سازی

(با استفاده از الگوریتم جستجوی اول سطح)

class FlowNetwork(object):
    def __init__(self):
        self.adj, self.flow, = {},{}

    def add_vertex(self, vertex):
        self.adj[vertex] = []

    def get_edges(self, v):
        return self.adj[v]

    def add_edge(self, u,v,w=0):
        self.adj[u].append((v,w))
        self.adj[v].append((u,0))
        self.flow[(u,v)] = self.flow[(v,u)] = 0

    def find_path(self, source, sink, path):
        if source == sink:
            return path
        for vertex, capacity in self.get_edges(source):
            residual = capacity - self.flow[(source,vertex)]
            edge = (source,vertex,residual)
            if residual> 0 and not edge in path:
                result = self.find_path(vertex, sink, path + [edge])
                if result != None:
                    return result

    def max_flow(self, source, sink):
        path = self.find_path(source, sink, [])
        while path != None:
            flow = min(r for u,v,r in path)
            for u,v,_ in path:
                self.flow[(u,v)] += flow
                self.flow[(v,u)] -= flow
            path = self.find_path(source, sink, [])

        return sum(self.flow[(source, vertex)] for vertex,capacity in self.get_edges(source))

مثال عملی

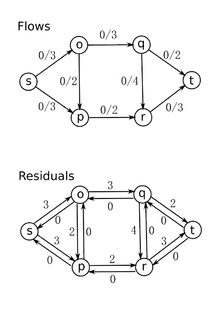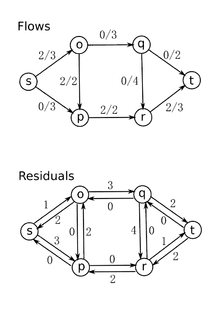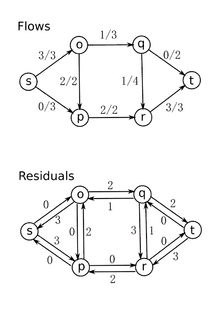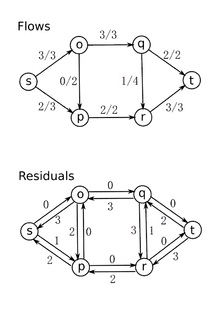
>>> g = FlowNetwork()
>>> [g.add_vertex(v) for v in "sopqrt"]
[None, None, None, None, None, None]
>>>
>>> g.add_edge('s','o',3)
>>> g.add_edge('s','p',3)
>>> g.add_edge('o','p',2)
>>> g.add_edge('o','q',3)
>>> g.add_edge('p','r',2)
>>> g.add_edge('r','t',3)
>>> g.add_edge('q','r',4)
>>> g.add_edge('q','t',2)
>>> print (g.max_flow('s','t'))
5

منابع

• مقدمه‌ای بر الگوریتم‌ها - پدیدآورنده: تامس کورمن، چارلز لیزرسان، رونالد دیوست، کلیفورد اشتاین - گروه مهندسی-پژوهشی خوارزمی (مترجم) - ناشر: درخشش
• ریاضیات گسسته و الگوریتم ها-پدیدآورنده:علی بهفروز، محمد ایزدی-ناشر:آییژ

پیوندهای کمکی

• Animation of Ford-Fulkerson algorithm (Java applet)

پرونده‌های رسانه‌ای مربوط به Ford-Fulkerson's algorithm در ویکی‌انبار