مسئله بیشینه جریان

در تئوری بهینه‌سازی، مسائل بیشینه جریان شامل پیدا کردن یک جریان عملی بیشینه از داخل یک شبکهٔ جریان تک-مبدأ و تک-مقصد است.
می‌توان به مسئلهٔ بیشینه جریان، به صورت حالت خاصی از مسائل پیچیده‌تر شبکهٔ جریان، مانند مسئلهٔ گردش، نگاه کرد. مقدار ماکسیمم یک جریان s-t (جریان از مبدأ به مقصد) برابر حداقل ظرفیت یک برش s-t (برشی که مبدأ را از مقصد جدا می‌کند) در شبکه است، همان‌طور که در قضیهٔ جریان بیشینه-برش کمینه ذکر شده است.

مثالی از یک شبکهٔ جریان با بیشینه جریان. مبدأ ${\displaystyle s}$ و مقصد ${\displaystyle t}$ است. اعداد نمایانگر جریان و ظرفیت اند.

تاریخچه

مسئلهٔ بیشینهٔ جریان ابتدا توسط T. E. Harris و F. S. Ross در سال ۱۹۵۴ به عنوان مدل ساده شده‌ای از جریان رفت و آمد خط آهن شوروی مطرح شد. در ۱۹۵۵، .Lester R. Ford, Jr و Delbert R. Fulkerson اولین الگوریتم شناخته شده، الگوریتم فورد–فالکرسون را ایجاد کردند.
در طول زمان، تعداد زیادی راه حل بهبود یافته برای مسئلهٔ بیشینهٔ جریان پیدا شده است، به ویژه الگوریتم کوتاه‌ترین راه افزوده از Edmonds و Karp و به صورت مستقل از Dinitz، الگوریتم سد کردن جریان Dinitz، الگوریتم ارسال-برچسب Goldberg و Tarjan، و الگوریتم سد کردن دودویی جریان از Goldberg و Rao. الگوریتم جریان الکتریکی Madry، Kelner، Christano و Spielman یک جریان بیشینهٔ تقریباً بهینه می‌یابد اما فقط در گراف‌های بدون جهت کار می‌کند.

تعریف

یک شبکهٔ جریان با مبدأ ${\displaystyle s}$ و مقصد ${\displaystyle t}$. اعداد کنار یال‌ها ظرفیت هستند.

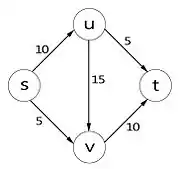
فرض کنید ${\displaystyle \scriptstyle N=(V,E)}$ یک شبکه است با ${\displaystyle \scriptstyle s,t\in V}$ که به ترتیب مبدأ و مقصد هستند.

ظرفیت یک یال، نگاشت ${\displaystyle \scriptstyle c:E\to \mathbb {R} ^{+}}$ است که با ${\displaystyle \scriptstyle c_{uv}}$ یا ${\displaystyle \scriptstyle c(u,v)}$ نمایش داده می‌شود، و نشان دهندهٔ بیشینه مقدار جریانی است که می‌تواند از یال بگذرد.

یک جریان، نگاشت ${\displaystyle \scriptstyle f:E\to \mathbb {R} ^{+}}$ است که با ${\displaystyle \scriptstyle f_{uv}}$ یا ${\displaystyle \scriptstyle f(u,v)}$ نمایش داده می‌شود و دارای دو شرط زیر است:

1. ${\displaystyle \scriptstyle f_{uv}\leq c_{uv}}$ به ازای هر ${\displaystyle \scriptstyle (u,v)\in E}$ (شرط ظرفیت: جریان یک یال نمی‌تواند از ظرفیتش بیشتر باشد)
2. ${\displaystyle \scriptstyle \sum _{u:(u,v)\in E}f_{uv}=\sum _{u:(v,u)\in E}f_{vu}}$ به ازای هر ${\displaystyle \scriptstyle v\in V\setminus \{s,t\}}$ (بقای جریان‌ها: جمع جریان‌های ورودی یک رأس باید با جمع جریان‌های خروجی از آن برابر باشد، به جز در رأس‌های مبدأ و مقصد)

مقدار جریان به صورت ${\displaystyle \scriptstyle |f|=\sum _{v:(s,v)\in E}f_{sv}}$ تعریف می‌شود که ${\displaystyle s}$، مبدأ ${\displaystyle N}$ است. مقدار جریان، نشان‌دهندهٔ میزان جریان گذرنده از مبدأ به مقصد است.

مسئلهٔ بیشینه جریان، بیشینه کردن ${\displaystyle \scriptstyle |f|}$ است، یعنی هدایت بیش‌ترین جریان ممکن از ${\displaystyle s}$ به ${\displaystyle t}$.

راه‌حل‌ها

می‌توان گراف باقیمانده را تعریف کرد تا راهی اصولی برای جستجو کردن عملیات‌های جلو-عقب برای یافتن بیشینه جریان فراهم کند.
اگر شبکهٔ جریان ${\displaystyle G}$ و جریان ${\displaystyle f}$ روی ${\displaystyle G}$ را داشته باشیم، ${\displaystyle \scriptstyle G_{f}}$، گراف باقیماندهٔ ${\displaystyle G}$ را با توجه به ${\displaystyle f}$ اینگونه تعریف می‌کنیم:

1. مجموعه رأس‌های ${\displaystyle \scriptstyle G_{f}}$ همانند ${\displaystyle G}$ است.
2. هر رأس ${\displaystyle \scriptstyle e=(u,v)}$ از ${\displaystyle \scriptstyle G_{f}}$، دارای ظرفیت ${\displaystyle \scriptstyle c_{e}-f(e)}$ است.
3. هر رأس ${\displaystyle \scriptstyle e'=(v,u)}$ از ${\displaystyle \scriptstyle G_{f}}$، دارای ظرفیت ${\displaystyle \scriptstyle f(e)}$ است.

الگوریتم‌های حل مسئلهٔ بیشینه جریان در جدول زیر نشان داده شده‌است.

روش	پیچیدگی	توضیح
برنامه‌نویسی خطی	-	شرط‌ها توسط تعریف جریان مجاز داده شده‌اند. برنامهٔ خطی را اینجا ببینید.
الگوریتم فورد-فالکرسون	${\displaystyle O(E\max(|f|))}$	تا جایی که مسیری باز در گراف باقی مانده وجود دارد، کمینه ظرفیت‌های گراف باقی مانده را به مسیر می‌فرستد. این الگوریتم فقط زمانی کار می‌کند که همه وزن‌ها عدد صحیح باشند، در غیر این صورت ممکن است مقدار بیشینه برگردانده نشود.
الگوریتم Edmonds Karp	${\displaystyle O(VE^{2})}$	مدل خاصی از الگوریتم فورد-فالکرسون، که با جستجوی سطح اول مسیرهای اضافه شده را پیدا می‌کند.
الگوریتم سد جریان Dinitz	${\displaystyle O(V^{2}E)}$	این الگوریتم در هر مرحله یک گراف لایه‌ای را به وسیله جستجوی سطح اول روی گراف باقیمانده می‌سازد. بیشینه جریان در یک گراف لایه‌ای در (O(VE محاسبه می‌شود، و بیشترین تعداد مرحل n-1 است. الگوریتم دینیک در شبکه‌های دارای ظرفیت‌های واحد، در ${\displaystyle \scriptscriptstyle O(E{\sqrt {V}})}$ به پایان می‌رسد.
الگوریتم ارسال-برچسب عمومی	${\displaystyle O(V^{2}E)}$	الگوریتم ارسال-برچسب از یک پیش‌جریان (یک تابع جریان با امکان افزایش در رأس‌ها) پشتیبانی می‌کند. الگوریتم اجرا تا وقتی که رأسی با افزایش مثبت (یک رأس فعال در گراف) وجود دارد اجرا می‌شود. عمل push جریان را روی یک یال باقیمانده افزایش می‌دهد، و یک تابع ارتفاع روی رأس‌ها کنترل می‌کند که کدام یال باقیمانده می‌تواند push شود. استفادهٔ درست از این توابع تضمین می‌کنند که جریان به دست آمده یک جریان بیشینه است.
الگوریتم ارسال-برچسب عمومی همراه با قانون انتخاب رأس FIFO	${\displaystyle O(V^{3})}$	این الگوریتم همواره آخرین رأس فعال را انتخاب می‌کند و عمل push را تا زمانی که افزایش مثبت است یا یک یال باقیمانده مجاز از این رأس وجود دارد، انجام می‌دهد.
الگوریتم سد جریان Dinitz به همراه درخت پویا	${\displaystyle O(VE\log(V))}$	داده ساختار درخت پویا سرعت محاسبه بیشینه جریان را در گراف لایه‌ای تا ${\displaystyle \scriptscriptstyle O(Elog{V})}$ افزایش می‌دهد.
الگوریتم ارسال-برچسب عمومی همراه با درخت پویا	${\displaystyle O(VE\log(V^{2}/E))}$	این الگوریتم با توجه به تابع ارتفاع، درختی با اندازه محدود روی گراف باقی‌مانده می‌سازد. این درخت‌ها امکان اعمال push چندسطحی را فراهم می‌کنند.
الگوریتم سد جریان دودویی	${\displaystyle \scriptscriptstyle O(E\min(V^{2/3},{\sqrt {E}})\log(V^{2}/E)\log {U})}$	مقدار U به بیشینه ظرفیت شبکه وابسته است.
الگوریتم MPM (مخفف Pramodh-Kumar, Malhotra و Maneshwari)	${\displaystyle O(V^{3})}$	به مقالهٔ اصلی مراجعه کنید.
الگوریتم KRT + Jim Orlin's (مخفف Rao, King و Tarjan)	${\displaystyle O(VE)}$	الگوریتم Orlin مسئلهٔ بیشینه جریان را در زمان ${\displaystyle O(VE)}$ برای ${\displaystyle m\leq O(n^{(16/15)-\epsilon })}$ حل می‌کند در حالی که KRT آن را در زمان ${\displaystyle O(VE)}$ برای ${\displaystyle m>n^{1+\epsilon }}$ حل می‌کند.

قضیهٔ جریان انتگرال

قضیهٔ جریان انتگرال می‌گوید:

اگر هر یال در شبکهٔ جریان ظرفیت انتگرالی داشته باشد، آنگاه یک جریان ماکسیمال انتگرالی وجود دارد.

کاربرد

مسئلهٔ بیشینه جریان چند-مبدأ و چند-مقصد

شکل ۴٫۱٫۱. تبدیل یک مسئلهٔ بیشینه جریان چند-مبدأ چند-مقصد به یک مسئلهٔ بیشینه جریان تک-مبدأ تک-مقصد.

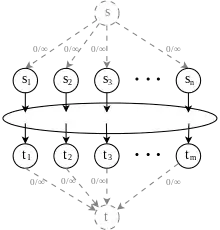
می‌خواهیم جریان بیشینه را روی شبکهٔ ${\displaystyle N=(V,E)}$ که دارای مجموعهٔ مبدأهای ${\displaystyle S=\{s_{1},...,s_{n}\}}$ و مجموعهٔ مقصدهای ${\displaystyle T=\{t_{1},...,t_{n}\}}$ (به جای تنها یک مبدأ و یک مقصد) است، پیدا کنیم. می‌توانیم مسئله چند-مبدأ و چند-مقصد را با افزودن یک مبدأ تثبیت شده که به تمام راس‌های ${\displaystyle S}$ متصل است و یک مقصد تثبیت شده که به تمام راس‌های ${\displaystyle T}$ متصل است (ابرمبدأ و ابرمقصد) و یال‌های آن‌ها ظرفیت بی‌نهایت دارند، به یک مسئلهٔ بیشینه جریان تبدیل کنیم.

کمینه پوشش مسیر در گراف جهت‌دار بدون دور

برای پیدا کردن کمینه تعداد مسیر‌ها برای پوشش دادن تمام رأس‌های ${\displaystyle V}$ در یک گراف جهت‌دار بدون دور ${\displaystyle G=(V,E)}$، می‌توانیم یک گراف دوبخشی ${\displaystyle G'=(V_{out}\in V_{in},E)}$ از ${\displaystyle G}$ بسازیم که:

1. ${\displaystyle V_{out}=\{v\in V\}}$ که درجهٔ خروجی هر ${\displaystyle v}$ مثبت است.
2. ${\displaystyle V_{in}=\{v\in V\}}$ که درجهٔ ورودی هر ${\displaystyle v}$ مثبت است.
3. ${\displaystyle E'=\{(u,v)\in (V_{out},V_{in}:(u,v)\in E\}}$.

آنگاه می‌توان با استفاده از نظریه کونیگ نشان داد که ${\displaystyle G'}$ یک تطابق با اندازهٔ ${\displaystyle m}$ دارد اگر و تنها اگر ${\displaystyle n-m}$ راه وجود داشته باشد که هر رأس در ${\displaystyle G}$ را پوشش می‌دهد و ${\displaystyle n}$ تعداد رأس‌های ${\displaystyle G}$ است؛ بنابراین مسئله را می‌توان با پیدا کردن تطابق ماکسیمم در ${\displaystyle G'}$ حل کرد.

تطابق بیشینهٔ دوبخشی

شکل ۴٫۳٫۱. تبدیل یک مسئلهٔ تطابق بیشینهٔ دوبخشی به مسئلهٔ بیشینه جریان.

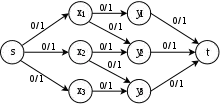
برای پیدا کردن تطابق بیشینه (تطابقی که بیش‌ترین تعداد رأس‌های ممکن را دارد) در یک گراف دو بخشی ${\displaystyle G=(X\cup Y,E)}$، می‌توانیم مسئله را با ساختن شبکهٔ ${\displaystyle N=(X\cup Y\cup \{s,t\},E')}$ به یک مسئلهٔ بیشینه جریان تبدیل کنیم، که:

1. ${\displaystyle E'}$ شامل یال‌هایی از ${\displaystyle G}$ است که جهتشان از ${\displaystyle X}$ به ${\displaystyle Y}$ است.
2. ${\displaystyle (s,x)\in E'}$ برای هر ${\displaystyle x\in X}$ و ${\displaystyle (y,t)\in E'}$ برای هر ${\displaystyle y\in Y}$.
3. ${\displaystyle c(e)=1}$ برای هر ${\displaystyle e\in E'}$ (شکل ۴٫۳٫۱ را ببینید).

آنگاه مقدار بیشینه جریان در ${\displaystyle N}$ برابر اندازهٔ تطابق ماکسیمم در ${\displaystyle G}$ است.

مسئلهٔ بیشینه جریان با ظرفیت رأس

شکل ۴٫۴٫۱. تبدیل یک مسئلهٔ تطابق بیشینهٔ جریان با شرط ظرفیت رأس‌ها به مسئلهٔ بیشینه جریان اصلی با بخش کردن رأس‌ها.

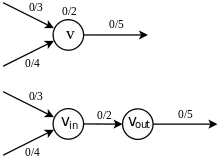
اگر شبکهٔ ${\displaystyle N=(V,E)}$ را داشته باشیم که در آن علاوه بر یال‌ها، هر رأس هم ظرفیت دارد، یعنی نگاشت ${\displaystyle c:V\mapsto \mathbb {R} ^{+}}$ که با ${\displaystyle c(v)}$ نمایش داده می‌شود به طوری که جریان f علاوه بر شرط ظرفیت و بقای جریان‌ها، شرط ظرفیت رأس را هم داشته باشد:

${\displaystyle \sum _{i\in V}f_{iv}\leq c(v)\qquad \forall v\in V\backslash \{s,t\}}$

به بیان دیگر مقدار جریانی که از یک رأس می‌گذرد نمی‌تواند از ظرفیت آن بیشتر باشد. برای یافتن ماکسیمم جریان در ${\displaystyle N}$ می‌توان با گسترش ${\displaystyle N}$، مسئله را به یک مسئلهٔ بیشینه جریان تبدیل کرد. ابتدا هر ${\displaystyle v\in V}$ با ${\displaystyle v_{\text{in}}}$ و ${\displaystyle v_{\text{out}}}$ جایگزین می‌شود که ${\displaystyle v_{\text{in}}}$ متصل به یال‌هایی است که به ${\displaystyle V}$ وارد می‌شود و ${\displaystyle v_{\text{out}}}$ متصل به یال‌هایی است که از آن خارج می‌شوند، سپس ظرفیت ${\displaystyle c(v)}$ را به یالی نسبت می‌دهیم که ${\displaystyle v_{\text{in}}}$ و ${\displaystyle v_{\text{out}}}$ را شامل می‌شود (شکل ۴٫۴٫۱ را ببینید، ولی در نظر داشته باشید که جای ${\displaystyle v_{\text{in}}}$ و ${\displaystyle v_{\text{out}}}$ به اشتباه در آن جابه‌جا شده‌است). در این شبکهٔ گسترش یافته، شرط ظرفیت رأس برداشته شده است؛ بنابراین می‌توان با این مسئله مانند یک مسئلهٔ بیشینه جریان برخورد کرد.

بیشینه مسیر مستقل

دو مسیر از هم مستقل اند اگر به جز ${\displaystyle s}$ و ${\displaystyle t}$ رأس مشترکی نداشته باشند. برای پیدا کردن بیشینه تعداد راه‌های مستقل از دو رأس ${\displaystyle s}$ به ${\displaystyle t}$ در گراف جهت‌دار ${\displaystyle G=(V,E)}$، می‌توان از ${\displaystyle G}$ دارای ظرفیت رأس، شبکهٔ ${\displaystyle N=(V,E)}$ را ساخت به طوری که:

1. ${\displaystyle s}$ و ${\displaystyle t}$ به ترتیب مبدأ و مقصد ${\displaystyle N}$ اند.
2. ${\displaystyle c(v)=1}$ برای هر ${\displaystyle v\in V}$.
3. ${\displaystyle c(e)=1}$ برای هر ${\displaystyle e\in E}$.

آنگاه مقدار بیشینه جریان برابر تعداد مسیرهای مستقل از ${\displaystyle s}$ به ${\displaystyle t}$ است.

بیشینه مسیر یال‌مجزا

برای پیدا کردن بیشینه تعداد مسیرهای یال‌مجزا از رأس ${\displaystyle s}$ به رأس ${\displaystyle t}$ در گراف جهت دار ${\displaystyle G=(V,E)}$، می‌توان مسئله را با ساختن شبکهٔ ${\displaystyle N=(V,E)}$ از ${\displaystyle G}$ با مبدأ ${\displaystyle s}$ و مقصد ${\displaystyle t}$ و نسبت دادن جریان واحد به هر یال، به یک مسئلهٔ بیشینه جریان تبدیل کرد.

بیشینه مسیر رأس‌مجزا

برای پیدا کردن بیشینه تعداد مسیرهای رأس‌مجزا از رأس ${\displaystyle s}$ به رأس ${\displaystyle t}$ در گراف جهت‌دار ${\displaystyle G=(V,E)}$، می‌توان مسئله را با ساختن شبکهٔ ${\displaystyle N=(V,E)}$ به صورت زیر، به یک مسئلهٔ بیشینه جریان تبدیل کرد:

1. هر رأس ${\displaystyle v}$ در گراف را به دو رأس ${\displaystyle v_{in}}$ و ${\displaystyle v_{out}}$ تقسیم کنید.
2. برای هر رأس ${\displaystyle v}$ یالی با ظرفیت یک از ${\displaystyle v_{in}}$ به ${\displaystyle v_{out}}$ اضافه کنید.
3. هر یال ${\displaystyle (u,v)}$ در گراف را با یالی از ${\displaystyle u_{out}}$ به ${\displaystyle v_{in}}$ با ظرفیت یک تعویض کنید.
4. یک رأس مقصد اختصاصی جدید به نام ${\displaystyle t}$ اضافه کنید.
5. برای هر رأس ${\displaystyle v}$، یالی از ${\displaystyle v_{in}}$ به ${\displaystyle t}$ با ظرفیت یک اضافه کنید.
6. یک بیشینه جریان از ${\displaystyle s_{out}}$ به t پیدا کنید. مقدار جریان برابر تعداد مسیرهای رأس‌مجزا است.

کاربردهای مسئله در دنیای واقعی

بازی‌های حذفی بیسبال

تشکیل شبکهٔ جریان برای مسئلهٔ بازی‌های حذفی بیسبال.

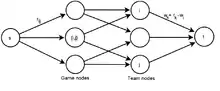
در این مسئله، ${\displaystyle n}$ تیم در یک لیگ به طور حذفی با یک‌دیگر مسابقه می‌دهند. در یک مرحلهٔ خاص، ${\displaystyle w_{i}}$ تعداد بردها، ${\displaystyle r_{i}}$ تعداد بازی‌های باقی‌مانده برای تیم ${\displaystyle i}$ام، و ${\displaystyle r_{ij}}$ تعداد بازی‌های باقی‌مانده در مقابل تیم ${\displaystyle j}$ام است. اگر تیمی شانس اول شدن از دست بدهد، از لیگ حذف خواهد شد. هدف این مسئله تعیین کردن تیم‌های حذف شده در هر زمان از فصل است. Schwartz برای این مسئله روشی پیشنهاد داد که این مسئله را به مسئلهٔ بیشینهٔ جریان تبدیل می‌کند. در این روش شبکه‌ای ساخته می‌شود که تعیین می‌کند آیا تیم ${\displaystyle k}$ حذف می‌شود یا نه.
فرض کنید گراف ${\displaystyle G=(V,E)}$ شبکه‌ای با ${\displaystyle s,t\in V}$ باشد که ${\displaystyle s}$ و ${\displaystyle t}$ به ترتیب مبدأ و مقصد را تعیین می‌کنند. یک رأس ${\displaystyle \{i,j\}}$ را به طوری که ${\displaystyle i<j}$ به گراف اضافه می‌کنیم و آن را با یالی با ظرفیت ${\displaystyle r_{ij}}$ به ${\displaystyle s}$ وصل می‌کنیم که تعداد بازی‌های بین دو تیم ${\displaystyle i}$ و ${\displaystyle j}$ را نشان می‌دهد. هم چنین برای هر تیم ${\displaystyle i}$ یک رأس ایجاد می‌کنیم و هر رأس ${\displaystyle \{i,j\}}$ را به رأس‌های ${\displaystyle i}$ و ${\displaystyle j}$ وصل می‌کنیم تا تضمین کنیم یکی از آن‌ها برنده می‌شود. برای این یال‌ها ظرفیتی تعیین نمی‌کنیم. در انتها، وزن یال بین تیم ${\displaystyle i}$ و مقصد ${\displaystyle t}$ را w_k+r_k–w_i قرار می‌دهیم تا تعداد بردهای تیم i از w_k+r_k تجاوز نکند. مجموعهٔ تیم‌های شرکت‌کننده در لیگ را ${\displaystyle S}$ می‌نامیم و ${\displaystyle \scriptstyle r(S-\{k\})=\sum _{i,j\in \{S-\{k\}\},i<j}r_{ij}}$. ادعا می‌کنیم تیم ${\displaystyle k}$ حذف نمی‌شود اگر و تنها اگر اندازهٔ جریانی با مقدار ${\displaystyle r(S-\{k\})}$ در شبکهٔ ${\displaystyle G}$ وجود داشته باشد. در مقالهٔ مذکور نشان داده شده که این مقدار همان مقدار بیشینهٔ جریان از ${\displaystyle s}$ به ${\displaystyle t}$ است.

برنامه‌ریزی خطوط هوایی

یکی از مسائل مهم در صنایع خطوط هوایی، برنامه‌ریزی برای خدمهٔ پرواز است. مسائل برنامه‌ریزی در خطوط هوایی می‌تواند به عنوان کاربردی از تعمیم مسئلهٔ بیشینهٔ جریان مطرح شود. ورودی مسئله، مجموعه‌ای از پروازها (${\displaystyle F}$) است که شامل مکان و زمان پروازهای ورودی و خروجی است. در یک مدل از برنامه‌ریزی، هدف این است که یک برنامه‌ریزی عملی صورت گیرد به طوری که حداکثر ${\displaystyle k}$ خدمه فعالیت کنند.
برای حل این مسئله، از مدل متفاوتی از مسئلهٔ گردش به نام گردش کراندار استفاده می‌کنیم، که مدل کلی‌ای از مسئلهٔ جریان است که در آن برای حداقل جریان منحصر با یال‌ها محدودیت قائل می‌شویم.
${\displaystyle G=(V,E)}$ را یک شبکه با مبدأ و مقصد ${\displaystyle s,t\in V}$ در نظر می‌گیریم. برای هر پرواز ${\displaystyle i}$، یک رأس ${\displaystyle s_{i}}$ برای مبدأ و یک رأس ${\displaystyle d_{i}}$ برای مقصد آن به ${\displaystyle V}$ اضافه می‌کنیم. هم چنین یال‌های زیر را به ${\displaystyle E}$ اضافه می‌کنیم:

1. یال‌هایی با ظرفیت [۰٬۱] بین ${\displaystyle s}$ و هر ${\displaystyle s_{i}}$
2. یال‌هایی با ظرفیت [۰٬۱] بین هر ${\displaystyle d_{i}}$ و ${\displaystyle t}$
3. یال‌هایی با ظرفیت [۰٬۱] بین هر جفت ${\displaystyle s_{i}}$ و ${\displaystyle d_{i}}$
4. یال‌هایی با ظرفیت [۰٬۱] بین هر ${\displaystyle d_{i}}$ و ${\displaystyle s_{j}}$، اگر بتوانیم با صرف هزینه و زمان معقول از ${\displaystyle d_{i}}$ به ${\displaystyle s_{j}}$ برسیم.
5. یالی با ظرفیت [∞,۰] بین ${\displaystyle s}$ و ${\displaystyle t}$

در روش ذکر شده، ادعا و اثبات می‌شود که پیدا کردن یک جریان با مقدار ${\displaystyle k}$ بین ${\displaystyle s}$ و ${\displaystyle t}$ در ${\displaystyle G}$، همان پیدا کردن برنامه‌ای عملی برای مجموعهٔ پروازهای ${\displaystyle F}$ با حداکثر ${\displaystyle k}$ خدمه است.
نوع دیگری از برنامه‌ریزی خطوط هوایی، پیدا کردن حداقل خدمه برای انجام شدن تمامی پروازهاست. برای پیدا کردن جواب این مسئله، یک گراف دو قسمتی ${\displaystyle G'=(A\cup B,E)}$ می‌سازیم که هر پرواز یک کپی در مجموعهٔ ${\displaystyle A}$ و مجموعهٔ ${\displaystyle B}$ دارد. اگر یک هواپیما بتواند پرواز ${\displaystyle j}$ را بعد از پرواز ${\displaystyle i}$ انجام دهد، ${\displaystyle i\in A}$ به ${\displaystyle j\in B}$ وصل می‌شود. یک تطابق در ${\displaystyle G'}$ شامل یک برنامه برای ${\displaystyle F}$ است و بدیهی است که حداکثر تطابق دوقسمتی در این گراف، یک برنامهٔ هوایی با حداقل تعداد خدمه را نشان می‌دهد. همان‌طور که در قسمت کاربردهای این مقاله ذکر شد، پیدا کردن تطابق بیشینه دوبخشی یکی از کاربردهای مسئلهٔ بیشینهٔ جریان است.

مسئلهٔ تقاضای گردش

تعدادی کارخانه هستند که کالا تولید می‌کنند و تعدادی دهکده هستند که باید به آن‌ها کالا برسد. آن‌ها با شبکه‌ای از جاده‌ها به هم متصل اند که هر جاده ظرفیت ${\displaystyle c}$ برای بیشینه کالایی که می‌تواند از آن بگذرد دارد. مسئله یافتن این است که آیا گردشی وجود دارد که تقاضا را برآورده کند یا خیر. این مسئله می‌تواند به یک مسئلهٔ بیشینه جریان تبدیل شود:

1. یک رأس مبدأ (${\displaystyle s}$) اضافه کنید و یال‌هایی از آن به هر رأس کارخانه (${\displaystyle f_{i}}$) با ظرفیت تولید ${\displaystyle p_{i}}$ اضافه کنید، که ${\displaystyle p_{i}}$ آهنگ تولید کارخانهٔ ${\displaystyle f_{i}}$ است.
2. یک رأس مقصد (${\displaystyle t}$) اضافه کنید و یال‌هایی از هر رأس دهکده (${\displaystyle v_{i}}$) با ظرفیت ${\displaystyle d_{i}}$ به آن اضافه کنید، که ${\displaystyle d_{i}}$ میزان تقاضای دهکده است.

${\displaystyle G=(V,E)}$ این شبکهٔ جدید است. گردشی وجود دارد که تقاضا را برآورده کند اگر و تنها اگر:
${\displaystyle Maximumflowvalue(G)=\sum _{i\in v}d_{i}}$
اگر یک گردش وجود داشته باشد، مسئلهٔ بیشینه جریان جواب این که چه مقدار کالا برای برآورده شدن تقاضا باید از طریق یک جادهٔ خاص فرستاده شود را به ما می‌دهد.

عدالت در اشتراک اتومبیل

مسئله این است که ${\displaystyle N}$ نفر از یک ماشین در ${\displaystyle k}$ روز به صورت اشتراکی استفاده می‌کنند. هر شرکت کننده می‌تواند در هر روز انتخاب کند که شرکت می‌کند یا خیر. هدف ما این است که عادلانه تصمیم بگیریم که در یک روز مشخص، چه کسی رانندگی می‌کند. راه حل به این صورت است:
می‌توانیم بر اساس تعداد افرادی که از ماشین استفاده می‌کنند تصمیم بگیریم، یعنی اگر ${\displaystyle m}$ نفر از ماشین در یک روز استفاده می‌کنند، هر نفر به مقدار ${\displaystyle 1/m}$ مسئولیت دارد؛ بنابراین برای هر شخص ${\displaystyle i}$، اجبار رانندگی (${\displaystyle D_{i}}$) به صورتِ ذکر شده است؛ بنابراین، شخص ${\displaystyle i}$ فقط باید ${\displaystyle [D_{i}]}$ بار در ${\displaystyle k}$ روز رانندگی کند.
هدف این است که پی ببریم آیا چنین وضعیتی امکان‌پذیر است یا خیر. برای این منظور همان‌طور که در شکل نشان داده شده است، سعی می‌کنیم مسئله را به یک شبکه تبدیل کنیم.
حال می‌توان ثابت کرد که اگر جریان ${\displaystyle k}$ وجود داشته باشد، آنگاه چنین وضعیت عادلانه‌ای و چنین جریانی با مقدار ${\displaystyle k}$ همواره وجود دارد.

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Maximum flow problem». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۱۵ مه ۲۰۰۹.

جستارهای وابسته

• بیشینه جریان