مرتب‌سازی ادغامی

مرتب‌سازی ادغامی
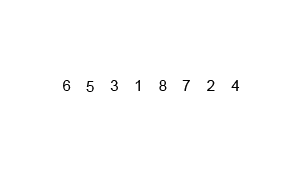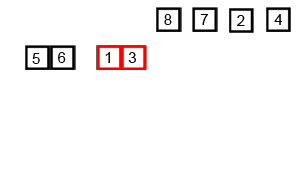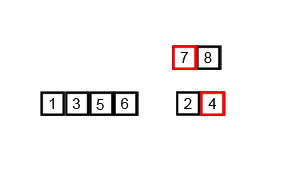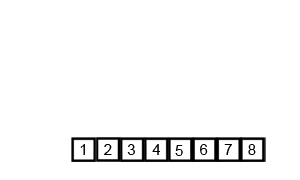	یک نمونه از مرتب‌سازی ادغامی. نخست فهرست را بر کوچک‌ترین واحد (۱ عنصر) تقسیم می‌کنیم، سپس هر عنصر را با فهرست مجاور مقایسه می‌کنیم تا دو فهرست مجاور مرتب و ادغام شوند. در نهایت همهٔ عناصر مرتب و ادغام شده‌اند.
رده	الگوریتم مرتب‌سازی
ساختمان داده	آرایه
کارایی بدترین حالت
کارایی بهترین حالت	معمولی، گونه طبیعی
کارایی متوسط
پیچیدگی فضایی	کمکی

مرتب‌سازی ادغام (به انگلیسی: Merge sort) یک الگوریتم مرتب‌سازی تطبیقی با زمان اجرای $n\lg n$ می‌باشد. در اکثر پیاده‌سازی‌ها این الگوریتم پایدار می‌باشد. بدین معنی که این الگوریتم ترتیب ورودی‌های مساوی را در خروجی مرتب شده حفظ می‌کند. این یک مثال از الگوریتم تقسیم و تسخیر می‌باشد. این الگوریتم در سال ۱۹۴۵ توسط جان فون نویمان اختراع شده‌است.

نمایش مرتب‌سازی ادغامی

این روش تقریباً به صورت درختی عمل می‌کند و در واقع روش استفاده شده در آن روش تقسیم و حل است. الگوریتم آن در چند عمل زیر خلاصه می‌شود:

گرفتن آرایه و تقسیم آن به دو زیر آرایه مساوی (اگر طول آرایه عددی فرد باشد، طول یکی از زیر آرایه‌ها یک واحد بیشتر از دیگری می‌شود)
بازگشت به مرحلهٔ ۱ برای هر یک از زیر آرایه‌ها که طول آن بزرگ تر یا مساوی ۲ است
ادغام دو زیر آرایه

الگوریتم

از نظر مفهومی یک الگوریتم مرتب‌سازی ادغام بدین صورت کار می‌کند:

اگر طول لیست ۰ یا ۱ باشد آن پیش از این مرتب شده‌است در غیر این صورت
لیست نامرتب را به دو زیرلیست که اندازهٔ آن‌ها در حدود نصف سایز لیست اولیه‌است تقسیم می‌کند.
هر زیرلیست را به‌طور بازگشتی با صدا کردن merge sort مرتب می‌کند.
دو تا دوتا زیر لیست‌ها را از آخر ادغام می‌کند تا به یک لیست برسد.

مرتب‌سازی ادغام ۲ تا ایدهٔ اصلی را با هم ترکیب می‌کند تا زمان اجرایش تقویت شود.

یک لیست کوچک از گام‌های کم‌تری برای مرتب‌کردن نسبت به یک لیست بزرگ استفاده می‌کند.
یرای مرتب کردن دو لیست مرتب‌شده نسبت به دو لیست نامرتب گام‌های کمتری نیاز می‌باشد به عنوان مثال اگر این لیست‌ها مرتب باشند شما مجبور هستید تا هر لیست را فقط یکبار پیمایش کنید.

این الگوریتم بازگشتیست

مثال

مجموعه <A=<۵٬۲٬۴٬۷٬۱٬۳٬۲٬۶ را با استفاده از الگوریتم مرتب‌سازی ادغام مرتب کنید.

ابتدا این آرایه را نصف می‌کنیم پس دو آرایه به طول ۴ بدست می‌آید، که برابر است با (۵٬۲٬۴٬۷) و(۱٬۳٬۲٬۶) سپس این روال را تا جایی ادامه می‌دهیم که که طول آرایه‌هایمان برابر یک شود؛ که برابر است با: (۶)(۲)(۳)(۱)(6)(۴)(۲)(۵) حال به صورت زیر آن‌ها را با هم ادغام می‌کنیم تا به آرایه اصلی مان برسیم.

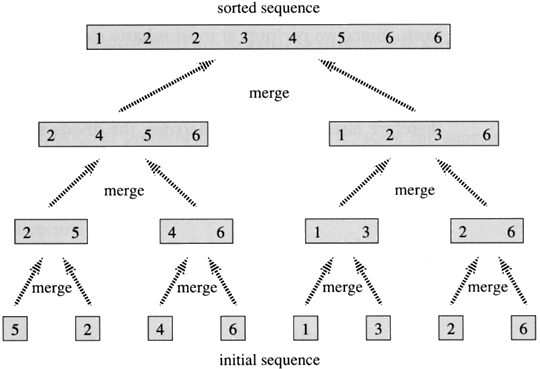
تحلیل

در مرتب کردن n تا عنصر مرتب‌سازی ادغام در حالت میانگین و بدترین حالت دارای زمان اجرای $nlgn$ می‌باشد. اگر زمان اجرای مرتب‌سازی ادغام برای یک لیست به طول $T(n),n$ باشد بنابراین رابطهٔ بازگشتی $T(n)=2T(n/2)+n$ از تعریف الگوریتم پیروی می‌کند. در این الگوریتم هر دفعه لیست را به دو زیرلیست تقسیم می‌کنیم و در هر مرحله n تا گام برای ادغام کردن لازم می‌باشد.

این شکل از رابطه، از قضیه اصلی واکاوی الگوریتم‌ها پیروی می‌کند. در بدترین حالت این الگوریتم تقریباً (n ⌈lg n⌉ - ۲^⌈lg n⌉ + ۱) مقایسه دارد که بین ((nlgn+n+O(n) و (nlgn-n+۱) می‌باشد. برای n بزرگ و یک لیست که به صورت تصادفی مرتب شده‌است یعنی ممکن است به هر ترتیبی باشد تعداد مقایسه مورد انتظار mergsort بهαn کمتر از بدترین حالت می‌رسد که α از رابطهٔ روبرو بدست می‌آید: $\alpha =-1+\sum _{k=0}^{\infty }{\frac {1}{2^{k}+1}}\approx 0.2645.$

در بدترین حالت تعداد مقایسه‌های مرتب‌سازی ادغام حدود ۰/۳۹ کمتر از مرتب‌سازی سریع در حالت متوسط می‌باشد. مرتب‌سازی ادغام همیشه تعداد مقایسه‌های کمتری را نسبت به مرتب‌ساز سریع احتیاج دارد، به جز در حالتی که تمام عناصر ورودی برابر باشند جایی که بدترین حالت مرتب‌سازی ادغام همراه با بهترین حالت مرتب‌سازی سریع پیدا می‌شود. پیچیدگی مرتب‌سازی ادغام در بدترین حالت از (O(nlgn می‌باشد که با بهترین حالت مرتب‌سازی سریع برابر می‌باشد اما در بهترین حالت تعداد مقایسه‌ها نصف تعداد مقایسه‌ها در بدترین حالت می‌باشد. در پیاده‌سازی بازگشتی مرتب‌سازی ادغام در بدترین حالت ۲n-۱ بار تابع مرتب‌سازی ادغام صدا زده می‌شود در حالی که در مرتب‌سازی سریع تابع مورد نیاز n بار صدا زده می‌شود. پیاده‌سازی غیر بازگشتی مرتب‌سازی ادغام از هزینهٔ سربار فراخوان تابع جلوگیری می‌کند که این کار سخت نمی‌باشد پیاده‌سازی رایج مرتب‌سازی ادغام به صورت درجا می‌باشد بنابراین سایز حافظه ورودی باید برای خروجی مرتب شده تخصیص داده شود. مرتب‌سازی درجا ممکن می‌باشد اما بسیار پیچیده‌است و در عمل از کارایی کمتری برخوردار می‌باشد حتی اگر در زمان nlgn اجرا شود. در این مواقع الگوریتم‌هایی شبیه مرتب‌سازی هرمی با سرعت قابل مقایسه پیشنهاد می‌شود که ازپیچیدگی کمتری برخوردار می‌باشد. برخلاف ادغام استاندارد ادغام درجا پایدار نیست.

ویژگی‌های مرتب‌سازی ادغامی

۱- پیچیدگی زمانی اجرای الگوریتم در تمامی حالات (Ө(n log n است. چرا که این الگوریتم تحت هر شرایطی آرایه را به دو قسمت کرده و مرتب‌سازی را انجام می‌دهد.

۲- پیچیدگی حافظه مصرفی بستگی به روش پیاده‌سازی مرحله ادغام دارد، که تا (O(n افزایش می‌یابد. پیاده‌سازی درجای این الگوریتم حافظه مصرفی مرتبه (Ө(۱ دارد. اما اجرای آن در بدترین حالت زمانبر است.

۳- الگوریتم مرتب‌سازی ادغامی با پیاده‌سازی فوق یک روش پایدار است. چنین الگوریتمی ترتیب عناصر با مقدار یکسان را پس از مرتب‌سازی حفظ می‌کند.

مقایسه با سایر الگوریتم‌ها

اگر چه مرتب‌سازی هرمی زمان اجرای مرتب‌سازی ادغام را دارد و فضای معین (Θ(۱ را در مقابل مرتب‌سازی ادغام که به فضای (Θ(nرا نیاز دارد دارا می‌باشد و آن در اغلب پیاده‌سازی‌های خاص سریع تر است و هم چنین اگر چه مرتب‌سازی سریع از نظر خیلی‌ها سریع‌ترین الگوریتم همه منظوره در نظر گرفته می‌شود اما در نگاه کلی مرتب‌سازی ادغام پایدار است و بهتر به صورت موازی جفت می‌کندو هم چنین در اداره کردن دستیابی به میانه‌های پشت سرهم کاراتر است.mergsort اغلب بهترین انتخاب برای مرتب کردن یک لیست پیوندی (Linked-List) می‌باشد در این موقعیت آسان است که مرتب‌سازی ادغام را به گونه‌ای پیاده‌سازی کنیم که آن فقط به فضای اضافه‌ای به اندازهٔ (Θ(۱ نیاز داشته باشد. کارایی دستیابی تصادفی یک لیست پیوندی باعث می‌شود تا بعضی از الگوریتم‌ها مانند مرتب‌سازی سریع ضعیف عمل کنند یا بعضی‌ها مانند مرتب‌سازی هرمی غیرممکن شود.

در یک شبه کد ساده الگوریتم به شکل زیر می‌باشد:

function merge_sort(m)
{
    var list left, right, result
    if length(m) <= 1
        return m
    // This calculation is for 1-based arrays. For 0-based, use length(m)/2
    var middle = length(m) / 2
    for each x in m up to middle
         add x to left
    for each x in m after middle
         add x to right
    left = merge_sort(left)
    right = merge_sort(right)
    result = merge(left, right)
    return result
}

function merge(left, right) {
    var list result
    while length(left)> 0 and length(right)> 0
        if first(left) <= first(right)
            append first(left) to result
            left = rest(left)
        else
            append first(right) to result
            right = rest(right)
    end while
    while length(left)> 0 
        append left to result
    while length(right)> 0
        append right to result
    return result}

زمان اجرا

اگر بخواهیم زمان اجرا را به صورت درختی محاسبه کنیم در زیر خواهیم داشت: T(n) = T( n/2 ) + T( n/2 ) + θ(n که برای سادگی: T(n) = 2T (n/2) + θ(n ]

نحوهٔ پیاده سازی الگوریتم

 
void mergeSort(int numbers[], int temp[], int array_size)
{
  m_sort(numbers, temp, 0, array_size - 1);
}

void m_sort(int numbers[], int temp[], int left, int right)
{
  int mid;

  if (right> left)
  {
    mid = (right + left) / 2;
    m_sort(numbers, temp, left, mid);
    m_sort(numbers, temp, mid+1, right);

    merge(numbers, temp, left, mid+1, right);
  }
}

void merge(int numbers[], int temp[], int left, int mid, int right)
{
  int i, left_end, num_elements, tmp_pos;

  left_end = mid - 1;
  tmp_pos = left;
  num_elements = right - left + 1;

  while ((left <= left_end) && (mid <= right))
  {
    if (numbers[left] <= numbers[mid])
    {
      temp[tmp_pos] = numbers[left];
      tmp_pos = tmp_pos + 1;
      left = left +1;
    }
    else
    {
      temp[tmp_pos] = numbers[mid];
      tmp_pos = tmp_pos + 1;
      mid = mid + 1;
    }
  }

  while (left <= left_end)
  {
    temp[tmp_pos] = numbers[left];
    left = left + 1;
    tmp_pos = tmp_pos + 1;
  }
  while (mid <= right)
  {
    temp[tmp_pos] = numbers[mid];
    mid = mid + 1;
    tmp_pos = tmp_pos + 1;
  }

  for (i=0; i <num_elements; i++)
  {
    numbers[right] = temp[right];
    right = right - 1;
  }
}

و مثالی از شبه کدی دیگر به زبان C

#include<;stdio.h>
#define SIZE 100

void mergesort(int, int a[]);
int main()
{
    int a[SIZE];
    int i, n;

    printf("No of elements to be sorted:\n");
    scanf("%d",&n);
    printf("Enter the elements:\n");
    for(i=0;i<n;i++)
    scanf("%d",&;a[i]);
    printf("Unsorted list:\n");
    for(i=0;i<n;i++)
    printf("%d",a[i]);
    printf("\n");
    mergesort(n, &;a);
    printf("Sorted list:\n");
    for(i=0;i<n;i++)
    printf("%d ",a[i]);
    printf("\n");
    return 0;
}
void mergesort(int n, int a[])
{
    int n1, n2, i, j, k;
    int a1[n];
    int *a2, *a3;
    for (i=0;i<n;i++)
    a1[i] = a[i];
    if (n%2 == 0)
    n1 = n/2;
    else
    n1 = n/2 + 1;
    n2 = n - n1;
    if (n>; 2)
    {
    mergesort(n1, &;a1);
    mergesort(n2, &;a1[n1]);
    }
    j = k = 0;
    a2 = &a1;
    a3 = &;a1[n1];
    for (i=0;i<n;i++)
    {
    if (k == n2)
    {
        a[i] = *(a2+j);
        j++;
    }
    else if (j == n1)
    {
        a[i] = *(a3+k);
        k++;
    }
    else if(*(a2+j) <;= *(a3+k))
    {
        a[i] = *(a2+j);
        j++;
    }
    else
    {
        a[i] = *(a3+k);
        k++;
    }
    }
}

شبه کد مرتب سازی ادغام به زبان پاسکال

Procedure Merg(idxLow, idxMid, idxHigh: Integer);
Var
  i, j, h, k: Integer;
Begin
  h := idxLow;
  i := idxLow;
  j := idxMid + 1;

  While ((h <= idxMid) And (j <= idxHigh)) Do
    Begin
      If (A[h] <A[j]) Then
        Begin
          B[i] := A[h];
          h := h + 1;
        End
      Else
        Begin
          B[i] := A[j];
          j := j + 1;
        End;
      i := i + 1;
    End;

  If (h> idxMid) Then
    Begin
      For k := j To idxHigh Do
        Begin
          B[i] := A[k];
          i := i + 1;
        End;
    End
  Else
    Begin
      For k := h To idxMid Do
        Begin
          B[i] := A[k];
          i := i + 1;
        End;
    End;

  For k := idxLow To idxHigh Do
    A[k] := B[k];
End;

Procedure MSort(Low_IDX, High_IDX: Integer);
Var
  Mid_IDX: Integer;
Begin
  If (Low_IDX <High_IDX) Then
    Begin
      Mid_IDX := (Low_IDX + High_IDX) Div 2;

      MSort(Low_IDX, Mid_IDX);
      MSort(Mid_IDX + 1, High_IDX);
      Merg(Low_IDX, Mid_IDX, High_IDX);
    End;
End;

منابع

مقدمه‌ای بر الگوریتم‌ها - پدیدآورنده: تامس کورمن، چارلز لیزرسان، رونالد دیوست، کلیفورد اشتاین - گروه مهندسی-پژوهشی خوارزمی (مترجم) - ناشر: درخشش

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

الگوریتم‌های مرتب‌سازی
تئوری	نظریه پیچیدگی محاسباتی نماد O بزرگ نماد امگا بزرگ ترتیب کامل الگوریتم مرتب‌سازی شبکه مرتب‌سازی مرتب‌سازی مقایسه‌ای
گونه‌های تعویضی	حبابی دست‌نشانده زوج و فرد ساختگی سریع شانه‌ای کوکتلی گورزاد
گونه‌های انتخابی	انتخابی دایره‌ای درخت دکارتی روان مسابقه‌ای هرمی
گونه‌های درجی	درجی درختی شکیبانه صدفی کتابخانه‌ای گسترده
گونه‌های ادغامی	ادغامی آبشاری ادغامی چندمرحله‌ای ادغامی نوسانی ادغامی رشته‌ای
گونه‌های توزیعی	انفجاری پایه‌ای پرچم آمریکا مجاور-نگاشت (پروکس‌مپ) سطلی شمارشی فلش لانه‌کبوتری مهره‌ای
گونه‌های همرو	ادغامی دسته‌ای فرد-زوج بایتونیک جفتی
گونه‌های دوگانه	آن‌شافل تیم جی‌سورت درونگرا گسترش‌یافته
گونه‌های دیگر	اسپاگتی توپولوژیکی کلوچه‌ای