مرتب‌سازی انتخابی

مرتب‌سازی انتخابی یکی از انواع الگوریتم مرتب‌سازی می‌باشد که جزو دستهٔ الگوریتم‌های مرتب‌سازی مبتنی بر مقایسه‌است. این الگوریتم دارای پیچیدگی زمانی از درجهٔ O(n²) است که به همین دلیل اعمال آن روی مجموعهٔ بزرگی از اعداد کارا به نظر نمی‌رسدو به‌طور عمومی ضعیفتر از نوع مشابهش که مرتب‌ساز درجی است عمل می‌کند. این مرتب‌سازی به دلیل سادگی اش قابل توجه‌است. کارایی آن برحسب تعداد ورودی‌ها در نمودار زیر نشان داده شده‌است.

مرتب‌سازی انتخابی

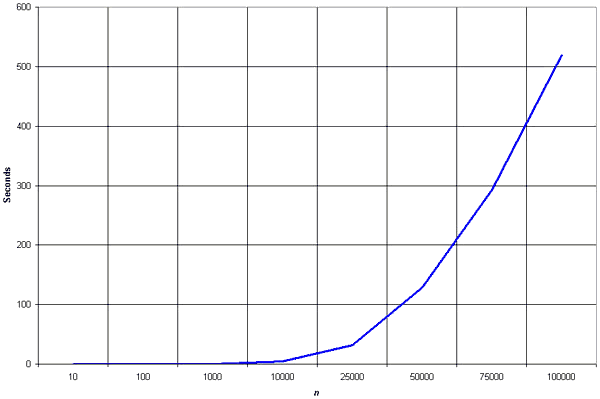
تجسم مرتب‌سازی انتخابی تجسم مرتب‌سازی انتخابی
رده	الگوریتم مرتب‌سازی
ساختمان داده	آرایه
کارایی بدترین حالت	${\displaystyle O(n^{2})}$
کارایی بهترین حالت	${\displaystyle O(n^{2})}$
کارایی متوسط	${\displaystyle O(n^{2})}$
پیچیدگی فضایی	${\displaystyle O(n)}$ مجموع، ${\displaystyle O(1)}$ کمکی

شکل (۱)
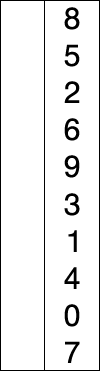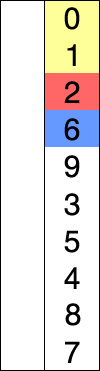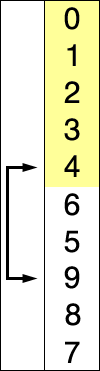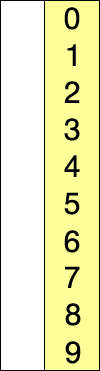
نحوهٔ عملکردمرتب‌سازی انتخابی

مرتب‌سازی انتخابی

نحوه عملکرد

این الگوریتم این‌گونه عمل می‌کند: ابتدا کوچکترین عنصر مجموعه اعداد را یافته با اولین عدد جابجا می‌کنیم. سپس دومین عنصر کوچکتر را یافته با دومین عدد جابجا می‌کنیم و این روند را برای n-1 عدد اول تکرار می‌کنیم. در حقیقت در هر مرحله ما لیست خود را به دو بخش تقسیم می‌کنیم. زیرلیست اول که قبلاً مرتب کرده‌ایم و سایر اعضای لیست که هنوز مرتب نشده‌است. در جدول زیر مثالی از پیاده‌سازی این روال بر روی ۶ عدد آمده‌است.

ورودی: ۳۴  ۱۵  ۴  ۱۲ ۵۵ ۲۴ 
۱) ۴  ۱۵  ۳۴  ۱۲  ۵۵  ۲۴
۲) ۴  ۱۲  ۳۴  ۱۵  ۵۵  ۲۴
۳) ۴  ۱۲  ۱۵  ۳۴  ۵۵  ۲۴
۴) ۴  ۱۲  ۱۵  ۲۴  ۵۵  ۳۴
۵) ۴  ۱۲  ۱۵  ۲۴  ۳۴  ۵۵ 

پیاده سازی الگوریتم در زبان های برنامه نویسی

الگوریتم در پایتون

A = [64, 25, 12, 22, 11]
for i in range(len(A)):
    min_idx = i
    for j in range(i+1, len(A)):
        if A[min_idx] > A[j]:
            min_idx = j 
    A[i], A[min_idx] = A[min_idx], A[i]
 
print ("Sorted array")
for i in range(len(A)):
   print("%d" % A[i], end="\t")

الگوریتم در جاوا

/**
* @param arr a[0] to a[n-1] is the array to sort
*/
private static void selectionSort(double arr[])
{
	for(int i= 0; i < arr.length - 1; i++) // (could  i < arr.length - 1 because single element is also min element)
		for(int j= i + 1; j < arr.length; j++)
			if(arr[i] > arr[j])
			{
				double temp= arr[i];
				arr[i]= arr[j];
				arr[j]= temp;
			}
}

الگوریتم درC++

# include <iostream.h>

void selectionSort(int *array,int length)//selection sort function 
{
	int i,j,min,minat;
	for(i=0;i<(length-1);i++)
	{
		minat=i;
		min=array[i];

      for(j=i+1;j<(length);j++) //select the min of the rest of array
	  {
		  if(min>array[j])   //ascending order for descending reverse
		  {
			  minat=j;  //the position of the min element 
			  min=array[j];
		  }
	  }
	  int temp=array[i] ;
	  array[i]=array[minat];  //swap 
	  array[minat]=temp;

	}

}

void printElements(int *array,int length) //print array elements
{
	int i=0;
	for(i=0;i<10;i++)
    cout<<array[i]<<endl;
}

void main()
{

	int a[]={9,6,5,23,2,6,2,7,1,8};   // array to sort 
    selectionSort(a,10);                 //call to selection sort  
	printElements(a,10);               // print elements 
}

تحلیل مرتبه الگوریتم

تحلیل الگوریتم مرتب‌سازی انتخابی برخلاف بسیاری از مرتب‌سازی‌های دیگر بسیار ساده‌است. زیرا که هیچ‌کدام از حلقه‌های آن به اعداد موجود در لیست ورودی بستگی ندارد. در مرحلهٔ اول به دست آوردن کمینه در لیست n عنصری نیاز به پیمودن کل n عدد و n – 1 مقایسه دارد و سپس باید کمینهٔ بدست آمده با اولین عدد جابجا شود. در مرحلهٔ بعدی به دست آوردن دومین کمینه در لیست 1 - n عنصری نیاز به پیمودن کل 1 - n عدد و 2 - n مقایسه دارد و کمینهٔ بدست آمده بادومین عدد جابجا شودو این روند ادامه پیدا می‌کند. پس کلاً تعداد مقایسه‌ها عبارتست از:

(n − 1) + (n − 2) +... + 2 + 1 = n(n − 1) / 2 ∈ Θ(n²)

مرتبهٔ این الگوریتم به دلیل عدم وابستگی آن به نحوهٔ ترتیب اعداد در بهترین، بدترین و حالت متوسط یکسان و برابر(Θ(n²

است.

ویژگی‌های مرتب‌سازی انتخابی

۱-با توجه به قطعه کد نوشته شده، ترتیب عناصر تغییری در عملکرد آن اینجا نمی‌کند. یعنی این الگوریتم برای داده‌های کاملاً مرتب، نامرتب تصادفی و مرتب معکوس به یک ترتیب عمل کرده و تمام مقایسه‌های محاسبه شده در رابطه فوق را انجام می‌دهد؛ بنابراین پیچیدگی این الگوریتم در بهترین حالت و حالت متوسط نیز (Θ(n2 است. ۲- مرتب‌سازی انتخابی یک روش مرتب‌سازی درجا است. یعنی عملیات مرتب‌سازی در داخل خود لیست و بدون نیاز به حافظه کمکی بزرگ انجام می‌گیرد. ۳- در پیاده‌سازی مرتب‌سازی انتخابی به روش فوق، اگر دو عنصر با مقدار بیشینه داشته باشیم، اولی انتخاب شده و به انتهای لیست منتقل می‌شود. در نتیجه ترتیب آن‌ها به هم می‌خورد؛ بنابراین این پیاده‌سازی روش پایدار نیست. در روش پایدار ترتیب عناصر با مقدار یکسان تغییر نمی‌کند. اما اگر در مقایسه عناصر آرایه به جای> از => استفاده کنید، مرتب‌سازی پایدار خواهد شد.

مقایسه با سایر الگوریتمهای مرتب‌سازی

این الگوریتم بین الگوریتم‌های با مرتبهٔ مرتب‌ساز انتخابی از مرتب‌ساز حبابی و مرتب‌ساز گورزاد (در حالت متوسط) بهتر عمل می‌کند. اما عموماً ضعیفتر ازمرتب‌ساز درجی است. یکی از شباهتهای مرتب‌ساز درجی به مرتب‌ساز انتخابی این است که در هر دو پس از پیمایش Kام مجموعه اعداد kعنصر اول در جای صحیح خود قرار گرفته‌اند. فایدهٔ مرتب‌ساز درجی این است که برای پیدا کردن عنصر x هر تعداد از اعداد را که نیاز است بررسی می‌کند. حال آنکه مرتب ساز انتخابی همه عناصر باقی‌مانده را بررسی می‌کند. به هر حال هر دو آن‌ها روی لیستهای کوچک بسیار سریع هستند. در نهایت اعمال مرتب‌ساز انتخابی روی لیستهایی با اندازه بزرگ به مراتب از مرتب‌ساز حبابی که روی ان لیستها با پیچیدگی زمانی (Θ(n log n عمل می‌کند ضعیف‌تر است.

سورس مرتب‌سازی انتخابی (Selection sort)

مثال

این سورس یک عدد گرفته و به تعداد همان عدد از ورودی دریافت می‌کند و آن‌ها را با روش. Selection sort مرتب می‌کند.

# include<stdio.h>
# include<conio.h>
# include<stdlib.h>

//----
void read_list(int a[],int n){
 int i;
 for(i=0;i<n;i++){
  printf("\n\n\t ENTER THE ELEMENT [%d] :: ",i);
  scanf("%d",&a[i]);
  }
}
//----
void print_list(int a[],int n){
 int i;
 for(i=۰;i<n;i++)
  printf("\t%d",a[i]);
}
//----
void select_sort(int a[],int n){
 int i,j,temp,min;
 for(i=۰;i<n;i++){
  min=i;
  for(j=i+1;j<n;j++)
   if(a[min]>a[j])
  min=j;
  temp=a[i];
  a[i]=a[min];
  a[min]=temp;
  printf("\n\n\t PASS %d :: ",i);
  print_list(a,n);
 }
}
//----
void main(){
 int a[20],n;
 clrscr();
 printf("\n\n\t ENTER THE ARRAY LENGTH :: ");
 scanf("%d",&n);
 read_list(a,n);
 printf("\n\n\t THE ARRAY ELEMENTS ARE AS FOLLOWS :: ");
 print_list(a,n);
 select_sort(a,n);
 printf("\n\n\t THE SORTED LIST IS :: ");
 print_list(a,n);
 getch();
}
//----

جستارهای وابسته

• الگوریتم‌های مرتب‌سازی

منابع

• کتاب مقدمه‌ای بر الگوریتمها(CLRS)

پیوند به بیرون

• Animated Sorting Algorithms: Selection Sort – graphical demonstration and discussion of selection sort
• Applet and source code
• Analyze Selection Sort in an online JavaScript IDE
• Selection Sort in C++
• Selection Sort Demonstration
• Pointers to selection sort visualizations
• C++ Program - Selection Sort بایگانی‌شده در ۱۲ مارس ۲۰۰۸ توسط Wayback Machine
• Selection sort explained and C++ source code