مرتب‌سازی مجاور-نگاشت

مرتب‌سازی مجاور-نگاشت (به انگلیسی: ProxmapSort) یک نوع الگوریتم مرتب‌سازی است که با دسته‌بندی آرایه ای از داده‌ها یا کلیدها به چند «زیر آرایه» (که در مرتب‌سازی سطلی، سطل نامیده می‌شوند) انجام می‌شود.

مرتب‌سازی مجاور-نگاشت
Insertion sorting into buckets during proxmap.
نمونه مرتب‌سازی یک لیست از اعداد تصادفی
ردهالگوریتم مرتب‌سازی
ساختمان دادهآرایه
کارایی بدترین حالت
کارایی بهترین حالت
کارایی متوسط
پیچیدگی فضایی
اعضای آرایه با توجه به مقدارشان در سطل متناظرشان قرار می‌گیرند.
در مرتب‌سازی سطلی بعد از پر شدن تمام سطل‌ها، عناصرِ هر سطل مرتب می‌شوند اما در این نوع مرتب‌سازی، درجِ یک عنصر در سطل به روش درج در مرتب‌سازی درجی انجام می‌شود. (عنصر در دستهٔ مرتب شده قرار می‌گیرد)

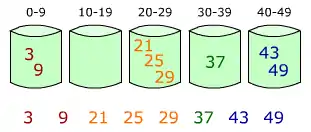
ریشهٔ نام این الگوریتم از «مجاورت» و «نگاشت» می‌آید. با یک «مجاورت نگاشتی» که برای هر کلید K شروع زیر آرایه (سطل) را نشان می‌دهد به طوری که K در ترتیب مرتب نهایی قرار گیرد. کلیدها با استفاده از روش مشابه در مرتب‌سازی درجی در هر سطل درج می‌شوند.

اگر کلیدها بین زیر آرایه‌ها «خوب توزیع شده» باشند، مرتب‌سازی در زمان خطی رخ می‌دهد.

می‌توان گفت این الگوریتم ترکیبی از مرتب‌سازی سطلی و مبنایی است.

پس از اتمام مرتب‌سازی مجاور-نگاشت، در صورتی که کلیدها خوب توزیع شده باشند، جستجوی مجاور-نگاشت می‌تواند کلید را در پیدا کند.

این دو الگوریتم در اواخر دهه ۱۹۸۰ توسط پروفسور توماس در دانشگاه کالیفرنیا، ارواین اختراع شد.

اساس روش الگوریتم

فرض کنید آرایه A با n تا کلید داده شده‌است:

  1. Initialize: 2 آرایه با اندازه n: hitCount , proxMap و ۲ آرایه A .l طول: مکان و A2 را ایجاد و اولیه کنید.
  2. پارتیشن: با استفاده از یک تابع MapKey با دقت انتخاب شده، A2 را با استفاده از کلیدها در A در زیرزمینها تقسیم کنید
  3. پراکندگی: بیش از A را بخوانید، و هر کلید را در سطل A2 خود قرار دهید. مرتب‌سازی درج در صورت لزوم
  4. جمع‌آوری: از زیر زمین‌ها به ترتیب بازدید کنید و تمام عناصر را به آرایه اصلی برگردانید، یا به سادگی از A2 استفاده کنید.

توجه: «کلیدها» همچنین ممکن است شامل داده‌های دیگری باشد، به عنوان مثال آرایه ای از اشیاء دانشجویی که شامل کلید به علاوه شناسه و نام دانشجو می‌باشد. این امر باعث می‌شود ProxMapSort برای سازماندهی گروه‌های اشیاء، نه فقط خود کلیدها، مناسب باشد.

مثال

یک آرایه کامل را در نظر بگیرید: A [0 تا n-1] با کلید N. بگذارید من یک فهرست از کلیدهای A. طبقه‌بندی A در آرایه A2 با اندازه مساوی باشم.

عملکرد کلید نقشه به صورت MapKey (کلید) = طبقه (K) تعریف شده‌است.

میز آرایه
A1 ۶٫۷ ۵٫۹ ۸٫۴ ۱٫۲ ۷٫۳ ۳٫۷ ۱۱٫۵ ۱٫۱ ۴٫۸ ۰٫۴ ۱۰٫۵ ۶٫۱ ۱٫۸
H ۱ ۳ ۰ ۱ ۱ ۱ ۲ ۱ ۱ ۰ ۱ ۱
P ۰ ۱ -۹ ۴ ۵ ۶ ۷ ۹ ۱۰ -۹ ۱۱ ۱۲
L ۷ ۶ ۱۰ ۱ ۹ ۴ ۱۲ ۱ ۵ ۰ ۱۱ ۷ ۱
A2 ۰٫۴ ۱٫۱ ۱٫۲ ۱٫۸ ۳٫۷ ۴٫۸ ۵٫۹ ۶٫۱ ۶٫۷ ۷٫۳ ۸٫۴ ۱۰٫۵ ۱۱٫۵

شبه کد

 
// compute hit counts
for i = 0 to 11 // where 11 is n
{
    H[i] = 0;
}
for i = 0 to 12 // where 12 is A.length
{
    pos = MapKey(A[i]);
    H[pos] = H[pos] + 1;
}

runningTotal = 0; // compute prox map – location of start of each subarray
for i = 0 to 11
    if H[i] = 0
        P[i] = -9;
    else
        P[i] = runningTotal;
        runningTotal = runningTotal + H[i];

for i = 0 to 12 // compute location – subarray – in A2 into which each item in A is to be placed
    L[i] = P[MapKey(A[i])];

for I = 0 to 12; // sort items
    A2[I] = <empty>;
for i = 0 to 12 // insert each item into subarray beginning at start, preserving order
{
    start = L[i]; // subarray for this item begins at this location
    insertion made = false;
    for j = start to (
! e end of A2 is found, and insertion not made | )
    {
        if A2[j] == <empty> // if subarray empty, just put item in first position of subarray
            A2[j] = A[i];
            insertion made = true;
        else if A[i] < A2[j] // key belongs at A2[j]
            int end = j + 1; // find end of used part of subarray – where first <empty> is
            while (A2[end] != <empty>)
                end++;
            for k = end -1 to j // move larger keys to the right 1 cell
                A2[k+1] = A2[k];
                A2[j] = A[i];
            insertion made = true; // add in new key
    }
}

در اینجا یک آرایه به مرتب است و توابع mapKey تعیین تعداد subarrays استفاده کنید. به عنوان مثال، کف (K) به سادگی به عنوان تعداد زیر قطعه به عنوان تعداد صحیح از داده‌ها در A اختصاص می‌دهد. تقسیم کلید به‌طور ثابت باعث می‌شود تعداد زیردریایی‌ها کاهش یابد. از توابع مختلف می‌توان برای ترجمه طیف وسیعی از عناصر در A به زیرزمینها، از جمله تبدیل حروف A-Z به ۰–۲۵ یا بازگشت شخصیت اول (۰–۲۵۵) برای مرتب‌سازی رشته‌ها استفاده کرد. زیر بخش‌ها به محض ورود داده‌ها طبقه‌بندی می‌شوند، نه بعد از قرار دادن تمام داده‌ها در زیرزمین، همان‌طور که در مرتب‌سازی سطل معمولی است.

جستجوی Proxmap

ProxmapSearch از آرایه proxMap تولید شده توسط ProxmapSort که قبلاً انجام شده‌است استفاده می‌کند تا بتواند کلیدها را در آرایه مرتب شده A2 در زمان ثابت پیدا کند.

استراتژی اساسی
  • مرتب کردن کلیدها با استفاده از ProxmapSort، نگه داشتن عملکرد MapKey و آرایه‌های P و A2
  • برای جستجوی یک کلید، به قسمت P [MapKey (k)]، شروع فرعی که حاوی کلید است، بروید، اگر این کلید در مجموعه داده‌ها باشد
  • پیاپی زیر زمین را جستجو کنید. اگر کلید پیدا شد، آن را بازگردانید (و اطلاعات مرتبط) اگر مقدار بیشتری از کلید پیدا کنید، کلید در مجموعه داده‌ها نیست
  • محاسبه P [MapKey (k)] طول می‌کشد زمان. اگر در هنگام مرتب‌سازی از یک کلید نقشه که توزیع خوبی از کلیدها دارد استفاده می‌شد، هر زیرانداز در بالا با یک c ثابت محدود می‌شود، بنابراین در بیشتر c مقایسه‌ها برای یافتن کلید یا دانستن وجود آن لازم است؛ بنابراین ProxmapSearch است . اگر از بدترین کلید نقشه استفاده شد، تمام کلیدها در یک زیرگذر یکسان هستند، بنابراین ProxmapSearch، در این بدترین حالت، به مقایسه

Pseudocode

 
function mapKey(key)
 return floor(key)
 proxMap ← previously generated proxmap array of size n
 A2 ← previously sorted array of size n
function proxmap-search(key)
 for i = proxMap[mapKey(key)] to length(array)-1
 if (sortedArray[i].key == key)
 return sortedArray[i]

کارایی

محاسبات H , P و L همه را در نظر می‌گیرد زمان. هر یک با یک گذر از یک آرایه محاسبه می‌شود، با زمان ثابت صرف شده در هر مکان آرایه.

  • بدترین حالت: MapKey همه موارد را در یک زیرسطح قرار می‌دهد، و در نتیجه مرتب‌سازی استاندارد و زمان زمان‌بندی درج می‌شود .
  • بهترین مورد: MapKey تعداد کمی از موارد مشابه را به ترتیب به جایی می‌دهد که بهترین مورد درج درج است. هر نوع درج است ، ج اندازه subarrays؛ بنابراین زیر قطعه p وجود دارد p * c = n، بنابراین مرحله درج O (n) را می‌گیرد؛ بنابراین، ProxmapSort است .
  • حالت متوسط: هر زیرانداز حداکثر اندازه c، یک ثابت است. مرتب‌سازی درج برای هر زیر قطعه سپس O (c ^ 2) در بدترین حالت - ثابت است. (زمان واقعی می‌تواند بسیار بهتر باشد، زیرا موارد c تا زمانی که آخرین مورد در سطل قرار نگیرد مرتب نشده‌اند). زمان کل تعداد سطل‌ها، (n / c)، بار است = .

داشتن یک عملکرد خوب MapKey برای جلوگیری از بدترین حالت ضروری است. ما باید چیزی در مورد توزیع داده‌ها بدانیم تا یک کلید خوب به وجود بیاید.

بهینه‌سازی
  1. صرفه جویی در وقت: مقادیر MapKey (i) را ذخیره کنید، بنابراین لازم نیست آنها دوباره حساب شوند (همان‌طور که در کد بالا وجود دارد)
  2. صرفه جویی در فضا: proxMaps را می‌توان در آرایه hitCount ذخیره کرد، زیرا به محاسبه تعداد پروگزما نیازی به شمارش ضربه نیست. اگر بخاطر داشته باشید که مقادیر A تاکنون مرتب شده‌اند، و داده‌ها می‌توانند به جای استفاده از A2، مرتب شوند.

پیاده‌سازی کد JavaScript: 

Array.prototype.ProxmapSort = function()
{//-- Edit date: 2019/11/13 Taiwan --//
  var start = 0;
  var end = this.length;
  var A2 = new Array(end);
  var MapKey = new Array(end);
  var hitCount = new Array(end);

  for (var i = start; i < end; i++){hitCount[i] = 0;}
  var min = this[start];
  var max = this[start];
  for (var i = start+1; i < end; i++){
    if (this[i] < min){min = this[i];}
    else{if (this[i] > max){max = this[i];}}
  }
  //Optimization 1.Save the MapKey[i].
  for (var i = start; i < end; i++){
    MapKey[i] = Math.floor(((this[i] - min ) / (max - min )) * (end - 1));
    hitCount[MapKey[i]]++;
  }
  //Optimization 2.ProxMaps store in the hitCount.
  hitCount[end-1] = end - hitCount[end-1];
  for (var i = end-1; i > start; i--){
    hitCount[i-1] = hitCount[i] - hitCount[i-1];
  }
  //insert A[i]=this[i] to A2 correct position
  var insertIndex = 0;
  var insertStart = 0;
  for (var i = start; i < end; i++){
    insertIndex = hitCount[MapKey[i]];
    insertStart = insertIndex;
    while(A2[insertIndex] != null){insertIndex++;}
    while(insertIndex > insertStart && this[i] < A2[insertIndex-1]){
      A2[insertIndex] = A2[insertIndex-1];
      insertIndex--;
    }
    A2[insertIndex] = this[i];
  }
  for (var i = start; i < end; i++){this[i] = A2[i];}
};

مقایسه با الگوریتم‌های مرتب‌سازی دیگر

از آنجا که ProxmapSort یک نوع مقایسه نیست، محدودیت پایین Ω (n log n) غیرقابل استفاده است. سرعت آن را می‌توان به این که نمی مبتنی بر مقایسه و با استفاده از آرایه به جای اشیاء پویا اختصاص داده و اشاره گر است که باید دنبال شود، مانند این است که با زمانی که با استفاده از یک انجام منسوب درخت جستجوی دودویی.

ProxmapSort امکان استفاده از ProxmapSearch را فراهم می‌کند. علی‌رغم زمان ساخت O (n)، ProxMapSearch با این کار می‌کند زمان دسترسی متوسط، و آن را برای بانکهای اطلاعاتی بزرگ بسیار جذاب می‌کند. اگر نیازی به به روزرسانی داده‌ها نباشد، زمان دسترسی ممکن است این عملکرد را نسبت به سایر انواع مبتنی بر مرتب‌سازی غیر مقایسه مقایسه کند.

نوع سطل عمومی مربوط به مرتب‌سازی پروکس-مپ

مانند ProxmapSort، سطل مرتب کردن بر اساس به‌طور کلی در یک لیست از n ورودی عددی بین صفر و برخی از کلید حداکثر یا ارزش M و تقسیم وسیعی ارزش به n سطل هر یک از اندازه M / N عمل می‌کند. اگر هر سطل با استفاده از مرتب‌سازی درج طبقه بندی شده باشد، ProxmapSort و مرتب‌سازی سطل می‌توانند در زمان خطی پیش‌بینی شده اجرا شوند.[1] با این حال، عملکرد این نوع تنزل با خوشه (یا بیش از حد چند سطل با بیش از حد بسیاری از کلیدهای)؛ اگر بسیاری از مقادیر در نزدیکی اتفاق بیفتد، همه در یک سطل واحد قرار می‌گیرند و عملکرد به شدت کاهش می‌یابد. این رفتار همچنین برای ProxmapSort حائز اهمیت است: اگر سطل‌ها خیلی بزرگ باشند، عملکرد آن به شدت کاهش می‌یابد.

منابع
  1. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001.
  • Thomas A. Standish. Data Structures in Java. Addison Wesley Longman, 1998. شابک ‎۰−۲۰۱−۳۰۵۶۴-X . Section 10.6, pp. 394–۴۰۵.
  • Standish, T. A.; Jacobson, N. (2005). "Using O(n) Proxmap Sort and O(1) Proxmap Search to motivate CS2 students (Part I)". ACM SIGCSE Bulletin. 37 (4). doi:10.1145/1113847.1113874.
  • Standish, T. A.; Jacobson, N. (2006). "Using O(n) Proxmap Sort and O(1) Proxmap Search to motivate CS2 students, Part II". ACM SIGCSE Bulletin. 38 (2). doi:10.1145/1138403.1138427.
  • Norman Jacobson "A Synopsis of ProxmapSort & ProxmapSearch" from Department of Computer Science, Donald Bren School of Information and Computer Sciences, UC Irvine.

پیوند به بیرون
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.